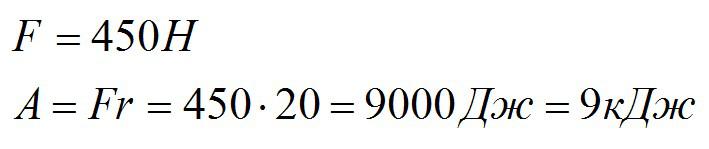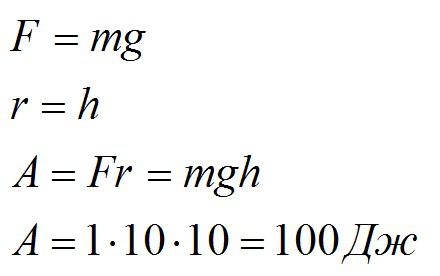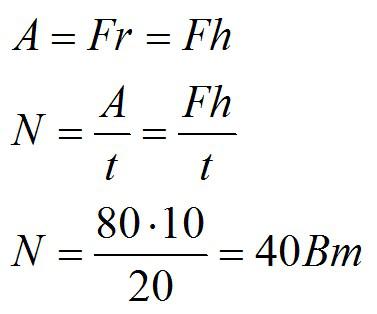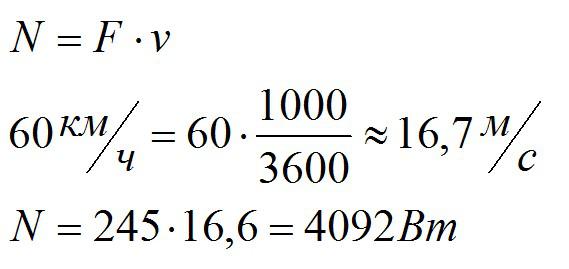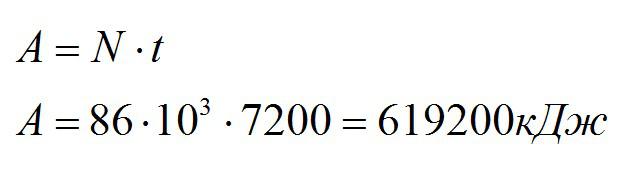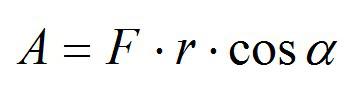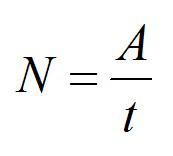Способ найти работу по физике

Механическая работа и мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа — мера воздействия силы.

Определение механической работы

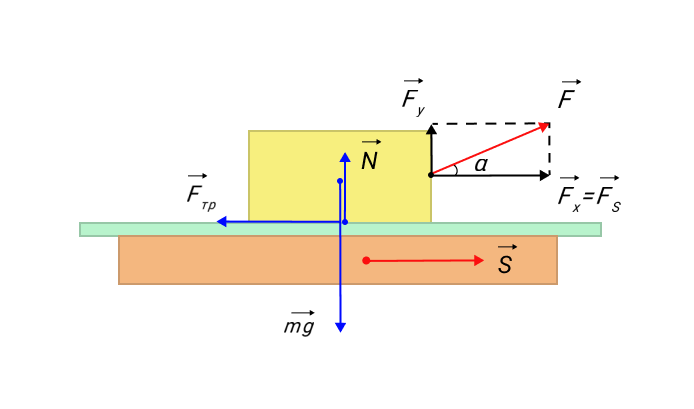
Работа А , совершаемая постоянной силой F → , — это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F → и перемещением s → .

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

Работа – это скалярная величина. Единица измерения работы по системе СИ — Джоуль ( Д ж ) .

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F → : A = F s cos α = F s s

При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:

A = ∑ ∆ A i = ∑ F s i ∆ s i .

Данная сумма работы вычисляется из предела ( Δ s i → 0 ) , после чего переходит в интеграл.

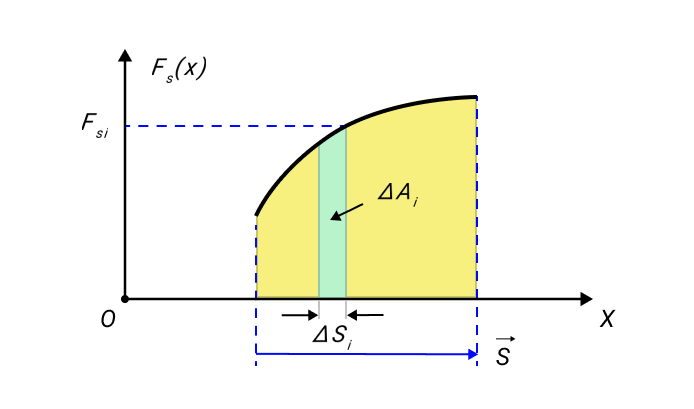
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s ( x ) рисунка 2.

Рисунок 2. Графическое определение работы Δ A i = F s i Δ s i .

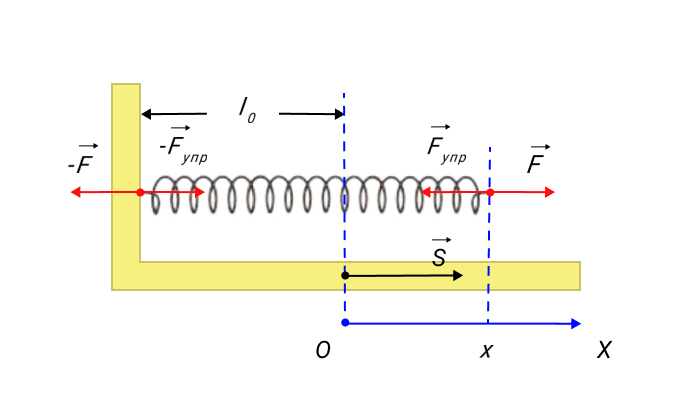
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.

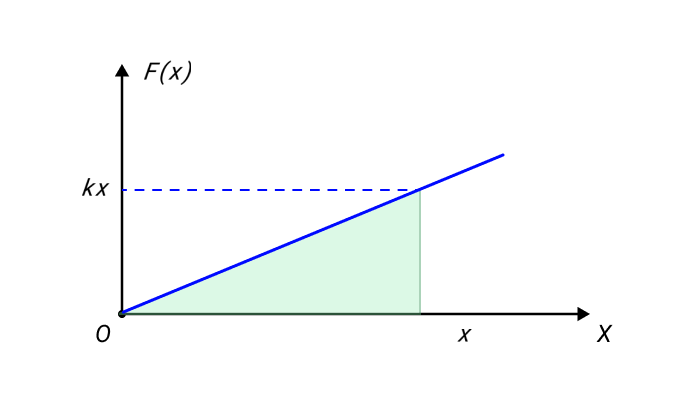
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.

Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Мощность

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

Система С И использует в качестве единицы мощности ватт ( В т ) . 1 Ватт — это мощность, которую совершает работу в 1 Д ж за время 1 с .

Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.

Источник

Задачи на расчет механической работы и механической мощности с решениями

• 12 января 2021 г.
• 6 минут
• 19 417

В сегодняшней статье кратко расскажем про работу и мощность в механике, а также приведем примеры задач для тех, кто учится их решать.

Больше полезной информации для студентов всех специальностей — на нашем телеграм-канале. Подписывайтесь!

Задачи на механическую работу и мощность с решениями

Задача №1. Нахождение механической работы

Условие

Грузчик равномерно толкает ящик с осциллографами по горизонтальному полу. Сила трения равна 450 Н. Найдите работу, совершенную грузчиком, если ящик передвинули на 20 метров.

Решение

Так как ящик двигался равномерно, то сила тяги грузчика равна силе трения.

Ответ: 9кДж

Задача №2. Расчет работы силы тяжести

Условие

Гантель массой 1 кг падает с высоты 10 метров. Какую работу совершает сила тяжести?

Решение

Ответ: 100 Дж.

mgh — выражение для потенциальной энергии камня в наивысшей точке.

Задача №3. Расчет механической мощности и работы

Условие

Деревенский житель поднимает ведро из колодца за 20 секунд, действуя с постоянной силой 80 Н. Глубина колодца равна h=10 м. Какую мощность развивает человек?

Решение

Сначала найдем работу, совершаемую при подъеме ведра, а затем вычислим мощность:

Ответ: 40 Вт.

Задача №4. Нахождение мощности. Связь мощности, силы и скорости

Условие

Мотороллер движется со скоростью 60 км/ч. Сила тяги двигателя равна 245 Н. Какую мощность развивает двигатель?

Решение

Переведем значение скорости в систему СИ и применим формулу, связывающую мощность, силу и скорость:

Ответ: 4092 Вт.

Задача №5. Нахождение механической работы.

Условие

Мощность двигателя трамвая равна 86 кВт. Какую работу может совершить трамвай за 2 часа непрерывной езды?

Решение

Работу можно вычислить из определения мощности:

Ответ: 619200 кДж

Вопросы на механическую мощность и работу

Вопрос 1. Сила тяжести действует на автомобиль, едущий по прямой и горизонтальной дороге. Совершает ли эта сила работу?

Ответ. Не совершает. Работу в данном случае совершает сила тяги двигателя автомобиля.

Вопрос 2. Приведите примеры механической работы.

Ответ. Примеры в которых совершается механическая работа:

• лошадь тянет телегу (работу совершает сила тяги лошади);
• бурлаки на Волге тянут баржу (работу совершает мускульная сила рук бурлаков);
• спортсмен поднимает штангу (работу совершает мускульная сила рук спортсмена).

Вопрос 3. Камень падает с неба. Совершает ли сила тяжести работу?

Ответ. Да, совершает. Это работа так называемых потенциальных, или диссипативных, сил.

Вопрос 4. Какие есть внесистемные единицы измерения мощности?

Ответ. Самая распространенная внесистемная единица измерения мощности — лошадиная сила.

1 лошадиная сила равна примерно 745 Ваттам.

Вопрос 5. Какая еще величина выражается в Джоулях?

Ответ. Джоуль — единица измерения не только работы, но и энергии.

Работа и мощность в механике

Работа в механике

Для работы существует множество определений. Нас в данном случае интересует лишь одно:

Механическая работа — скалярная физическая величина, равная произведению силы, действующей на тело, на модуль перемещения, которое совершает тело под действием этой силы.

Если направления векторов силы и перемещения не совпадают, в определение добавляется третий множитель: косинус угла альфа между векторами.

Единица измерения работы: Джоуль

Мощность в механике

Мощность показывает, какая работа совершается за единицу времени.

Механическая мощность — скалярная физическая величина, равная отношению работы ко времени, за которое она совершалась.

Мощность измеряется в Ваттах.

Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

• чтобы на тело действовала сила,
• чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Е_п = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

1. За счет чего происходит процесс?
2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости []

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

1. Выталкивающая сила.
2. Сила вязкого трения.
3. Сила тяжести.
4. Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

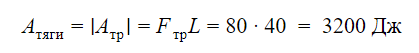
Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

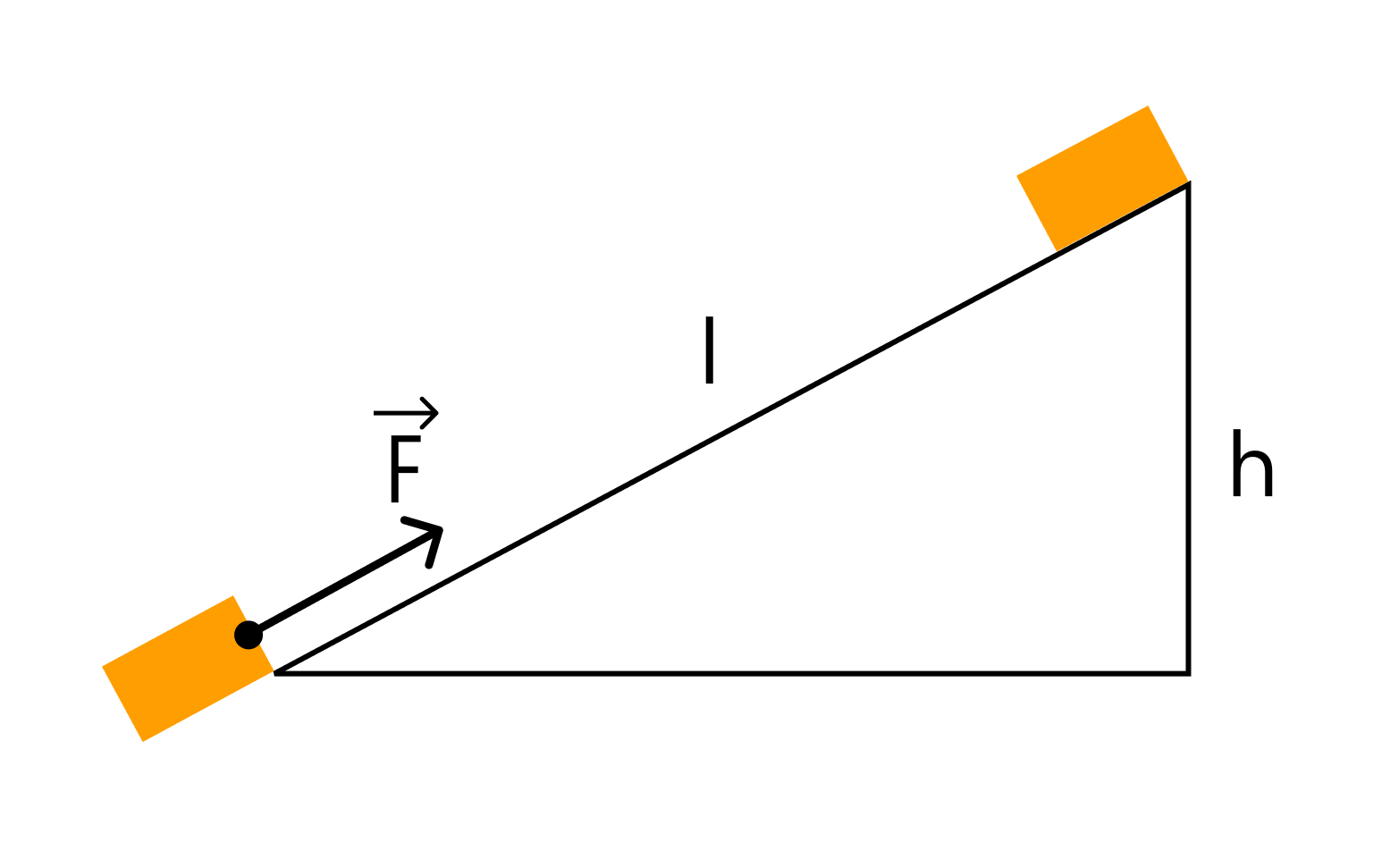
Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

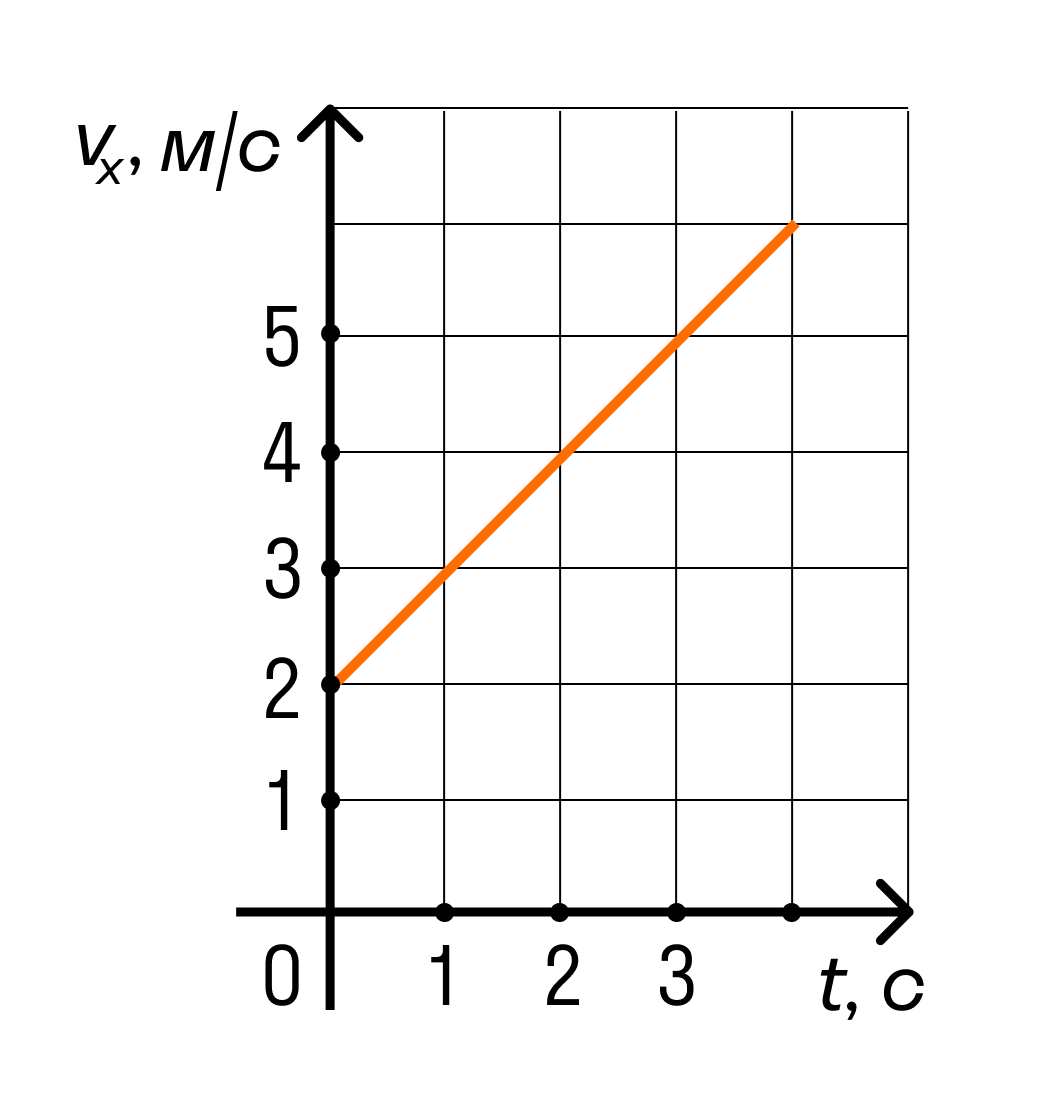
Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

Источник