Способ найти периметр прямоугольника

Периметр прямоугольника — формулы или способы расчетов

Началом пропедевтики изучения геометрии являются знания, которые учащиеся получают, переходя во 2 класс. Применяя правила умножения, здесь впервые вычисляют периметр прямоугольника.

Переходя в следующий, 3 класс, школьники на основе этой формулы начинают знакомиться с правилами раскрытия скобок.

Как вычислить периметр прямоугольника

Учитывая, что периметр любой фигуры есть сумма длин её сторон, выводят две формы записи для нахождения этой величины.

В прямоугольнике противоположные стороны равны, поэтому, обозначив смежные стороны a и b, получают по определению:

откуда после приведения подобных слагаемых, вытекает формула

или, вынося двойку за скобки,

Рассматривая квадрат, как прямоугольник с равными сторонами, получают формулу его периметра:

Стандартный метод

В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.

Задача

Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.

Решение

Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна

P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)

Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.

Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!

Часто длина заданного отрезка измеряется непосредственно.

Нахождение периметра через площадь и одну сторону

При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.

Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.

то есть, соотношение площади и периметра при известной стороне есть

Как найти периметр прямоугольной фигуры

В начальной школе для запоминания принципа детям часто предлагается понятие «неправильного четырёхугольника» (не прямоугольника).

Для нахождения его периметра предлагается рассчитать сумму длин сторон непосредственно, предварительно измерив каждую из них.

Для любой более сложной фигуры производят разбиение, если возможно, на небольшие прямоугольники, с которыми и работают.

Заключение

Современный онлайн калькулятор позволяет ввести значения сторон и задать необходимую точность вычислений, мгновенно производя расчёт и выдавая необходимый результат.

Источник

Как найти периметр прямоугольника

О чем эта статья:

Основные определения

Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра прямоугольника

Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.

Когда известны все или две соседние стороны

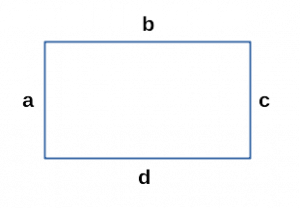
P = a + b + c + d, где a, b, c, d — стороны.

Когда известна любая сторона и площадь

P = 2 * (a + S : a), где a — сторона, S — площадь.

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Когда известна любая сторона и диагональ

P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Когда известна одна любая сторона и радиус описанной окружности

P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.

Радиус — отрезок, соединяющий центр и любую точку окружности.

Решение задач

А теперь практиковаться!

1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?

• Если a = 9, то b = 9 + 11;
• Тогда b = 20 см;
• Воспользуемся формулой P = 2 * (a + b);
• P = 2 * (9 + 20);

2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти длину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 60 : 15 = 4;
• Далее подставляем известные переменные в формулу: (15 + 4) * 2 = 38;

А еще можно вот так:

• Воспользуемся формулой P = 2 * (a + S : a);
• P = 2 * (15 + 60 : 15);

Ответ — такой же, 38 м.

3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?

• Если a = 8, то d = 8 *2;
• Тогда d = 16;
• Воспользуемся формулой P = 2 * (a + √(d 2 — а 2 ));
• P = 2 * (8 + √(16 2 — 8 2 ));

Источник

Периметр прямоугольника

Периметр прямоугольника — это сумма
всех сторон прямоугольника.

Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.

Самый простой способ найти периметр
прямоугольника, это сложить все стороны.

Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.

Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.

В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.

Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.

Формулы периметра прямоугольника

1. Периметр прямоугольника через четыре стороны
   

a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d;
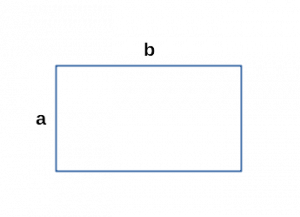
Периметр прямоугольника через смежные стороны

a, b — смежные стороны;
a ≠ b;
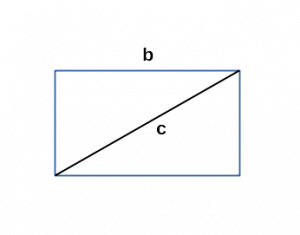
Периметр прямоугольника через любую сторону и диагональ

b — любая сторона;
c — диагональ;
Периметр прямоугольника через любую сторону и площадь

b — любая сторона;
S — площадь;
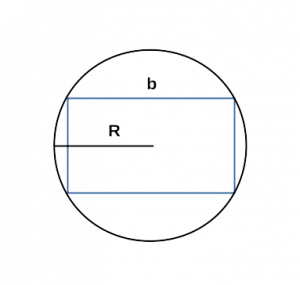
Периметр прямоугольника через любую сторону и радиус описанной окружности

b — любая сторона;
R — радиус описанной окружности;

Полупериметр

Полупериметр — это половина периметра.

Обозначается латинской буквой p.

Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.

\[ p = \frac

<2>= P \cdot 0.5 \]

Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.

Основные определения и величины

Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.

Обозначается латинской буквой a.

Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.

Обозначается латинской буквой b.

Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.

Обозначается латинской буквой a или b.

Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.

Обозначается латинской буквой c или d.

Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.

Обозначается латинской буквой l.

Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.

Обозначается латинской буквой R.

Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.

Обозначается латинской буквой h.

Источник

Периметры фигур. Периметр прямоугольника.

Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются

длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b)

Периметр прямоугольника ABCD равен сумме

сторон умноженной на 2, прилежащих к одному углу.

где P — периметр прямоугольника,

a — длина первой стороны,

b — длина второй стороны.

Как найти периметр прямоугольника другими способами? Ниже приведены формулы, по которым можно

найти периметр прямоугольника, через разные данные.

Формула периметра прямоугольника через две стороны прямоугольника:

Формула периметра прямоугольника через площадь и любую сторону:

Формула периметра прямоугольника через диагональ и любую сторону:

Формула периметра прямоугольника через радиус описанной окружности и любую сторону:

Формула периметра прямоугольника через диаметр описанной окружности и любую сторону:

Основные свойства прямоугольника.

• Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:

• Противоположные стороны прямоугольника параллельны:

• Прилегающие стороны прямоугольника всегда перпендикулярны:

AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB

• Все четыре угла прямоугольника прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

• Сумма углов прямоугольника равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

• Диагонали прямоугольника имеют одинаковой длины:

• Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:

2d 2 = 2a 2 + 2b 2

• Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на

• Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:

AO = BO = CO = DO = d/2

• Точка пересечения диагоналей называется центром прямоугольника и также является центром

• Диагональ прямоугольника является диаметром описанной окружности.

• Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов

равна 180 градусов:

∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°

• В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы

противоположных сторон не равны между собой (вписать окружность можно только в частный случай

Источник