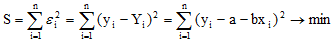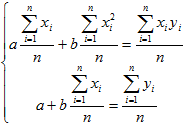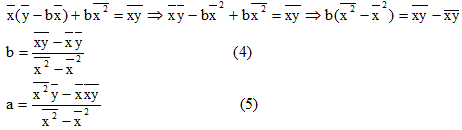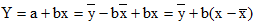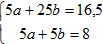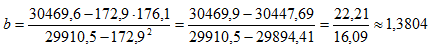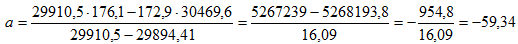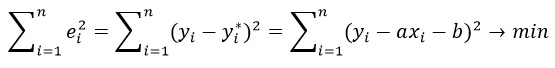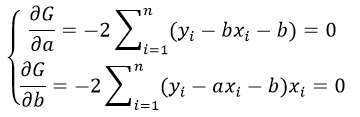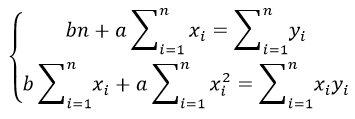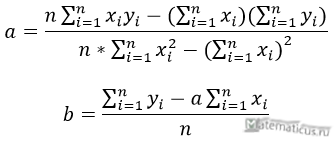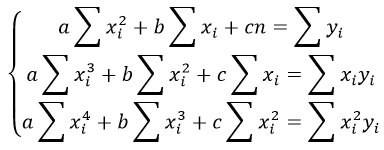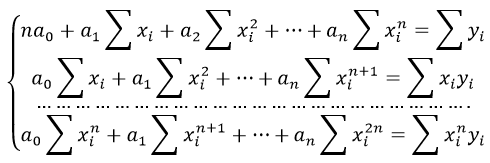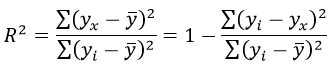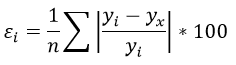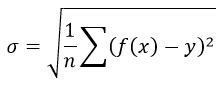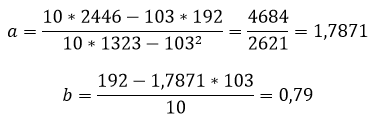Способ наименьших квадратов регрессия

Способ наименьших квадратов регрессия

При различных значениях а и b можно построить бесконечное число зависимостей вида y_x=a+bx т.е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов.

Линейную функцию a+bx ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значениям используем метод наименьших квадратов.

Обозначим: Y_i — значение, вычисленное по уравнению Y_i=a+bx_i. y_i — измеренное значение, ε_i=y_i-Y_i — разность между измеренными и вычисленными по уравнению значениям, ε_i=y_i-a-bx_i.

В методе наименьших квадратов требуется, чтобы ε_i, разность между измеренными y_i и вычисленными по уравнению значениям Y_i, была минимальной. Следовательно, находим коэффициенты а и b так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:

Исследуя на экстремум эту функцию аргументов а и с помощью производных, можно доказать, что функция принимает минимальное значение, если коэффициенты а и b являются решениями системы:

Если разделить обе части нормальных уравнений на n, то получим:

Учитывая, что 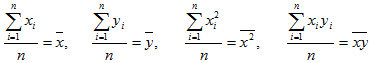(3)

Получим , отсюда , подставляя значение a в первое уравнение, получим: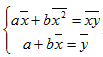

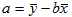
При этом b называют коэффициентом регрессии; a называют свободным членом уравнения регрессии и вычисляют по формуле:

Полученная прямая является оценкой для теоретической линии регрессии. Имеем:

Итак, 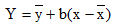является уравнением линейной регрессии.

Регрессия может быть прямой (b>0) и обратной (b 2 =4+0+1+4+16=25
x_iy_i=-2•0.5+0•1+1•1.5+2•2+4•3=16.5
y_i=0.5+1+1.5+2+3=8

и нормальная система (2) имеет вид

Решая эту систему, получим: b=0.425, a=1.175. Поэтому y=1.175+0.425x.

Пример 2. Имеется выборка из 10 наблюдений экономических показателей (X) и (Y).

xi	180	172	173	169	175	170	179	170	167	174
yi	186	180	176	171	182	166	182	172	169	177

Требуется найти выборочное уравнение регрессии Y на X. Построить выборочную линию регрессии Y на X.

Решение. 1. Проведем упорядочивание данных по значениям x_i и y_i. Получаем новую таблицу:

xi	167	169	170	170	172	173	174	175	179	180
yi	169	171	166	172	180	176	177	182	182	186

Для упрощения вычислений составим расчетную таблицу, в которую занесем необходимые численные значения.

xi	yi	xi 2	xiyi
167	169	27889	28223
169	171	28561	28899
170	166	28900	28220
170	172	28900	29240
172	180	29584	30960
173	176	29929	30448
174	177	30276	30798
175	182	30625	31850
179	182	32041	32578
180	186	32400	33480
∑xi=1729	∑yi=1761	∑xi 2 299105	∑xiyi=304696
x=172.9	y=176.1	xi 2 =29910.5	xy=30469.6

Согласно формуле (4), вычисляем коэффициента регрессии

Таким образом, выборочное уравнение регрессии имеет вид y=-59.34+1.3804x.
Нанесем на координатной плоскости точки (x_i; y_i) и отметим прямую регрессии.

На рис.4 видно, как располагаются наблюдаемые значения относительно линии регрессии. Для численной оценки отклонений y_i от Y_i, где y_i наблюдаемые, а Y_i определяемые регрессией значения, составим таблицу:

xi	yi	Yi	Yi-yi
167	169	168.055	-0.945
169	171	170.778	-0.222
170	166	172.140	6.140
170	172	172.140	0.140
172	180	174.863	-5.137
173	176	176.225	0.225
174	177	177.587	0.587
175	182	178.949	-3.051
179	182	184.395	2.395
180	186	185.757	-0.243

Значения Y_i вычислены согласно уравнению регрессии.

Заметное отклонение некоторых наблюдаемых значений от линии регрессии объясняется малым числом наблюдений. При исследовании степени линейной зависимости Y от X число наблюдений учитывается. Сила зависимости определяется величиной коэффициента корреляции.

Источник

Метод наименьших квадратов регрессия

Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид

y=ax+b

a, b – коэффициенты линейного уравнения регрессии;

x – независимая переменная;

y – зависимая переменная.

Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:

частные производные функции приравниваем к нулю

отсюда получаем систему линейных уравнений

Формулы определения коэффициентов уравнения линейной регрессии:

Также запишем уравнение регрессии для квадратной нелинейной функции:

Система линейных уравнений регрессии полинома n-ого порядка:

Формула коэффициента детерминации R 2 :

Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):

Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:

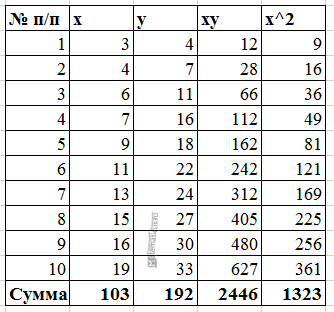
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:

x	y
3	4
4	7
6	11
7	16
9	18
11	22
13	24
15	27
16	30
19	33

Решение

Расчеты значений суммы, произведения x и у приведены в таблицы.

Расчет коэффициентов линейной регрессии:

при этом средняя ошибка аппроксимации равна:

ε=11,168%

Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:

y=1,7871x+0,79

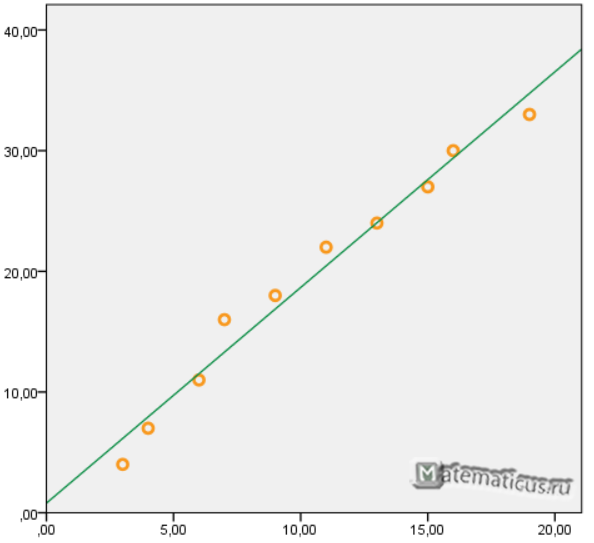
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек

Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 10

Источник