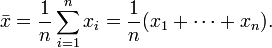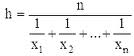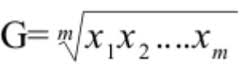Расчет среднего значения в программе Microsoft Excel
В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.
Стандартный способ вычисления
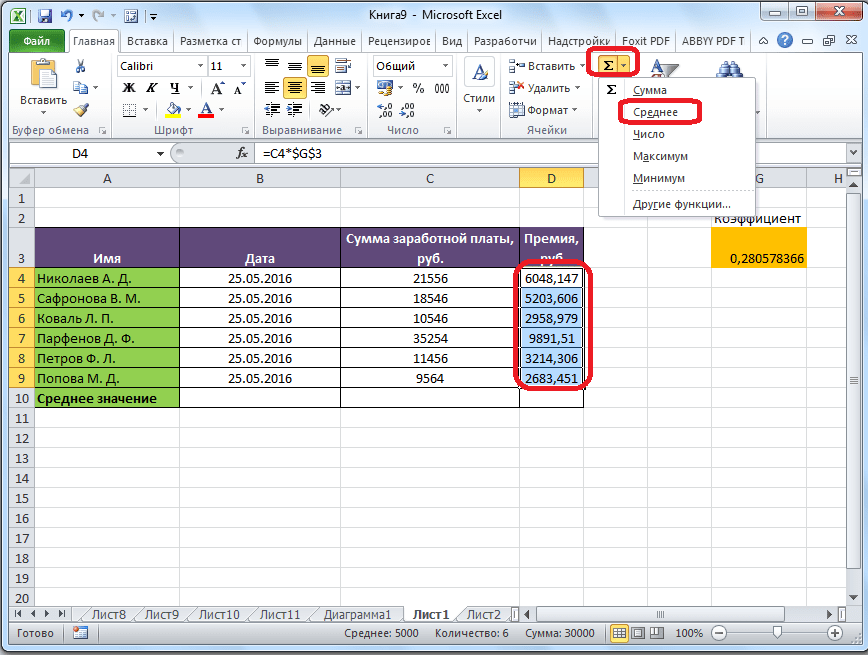
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».
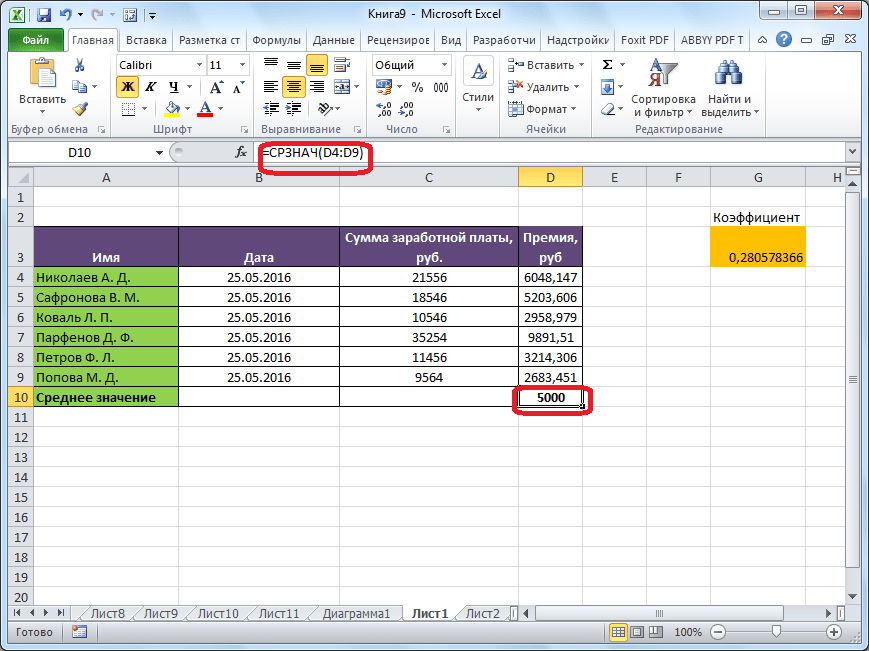
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.
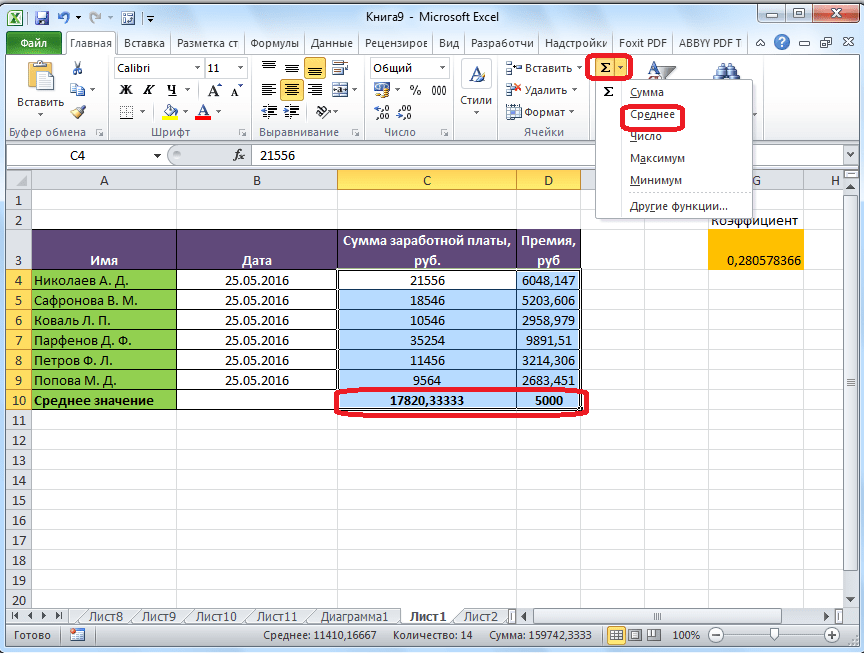
Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.
Вычисление с помощью Мастера функций
Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.
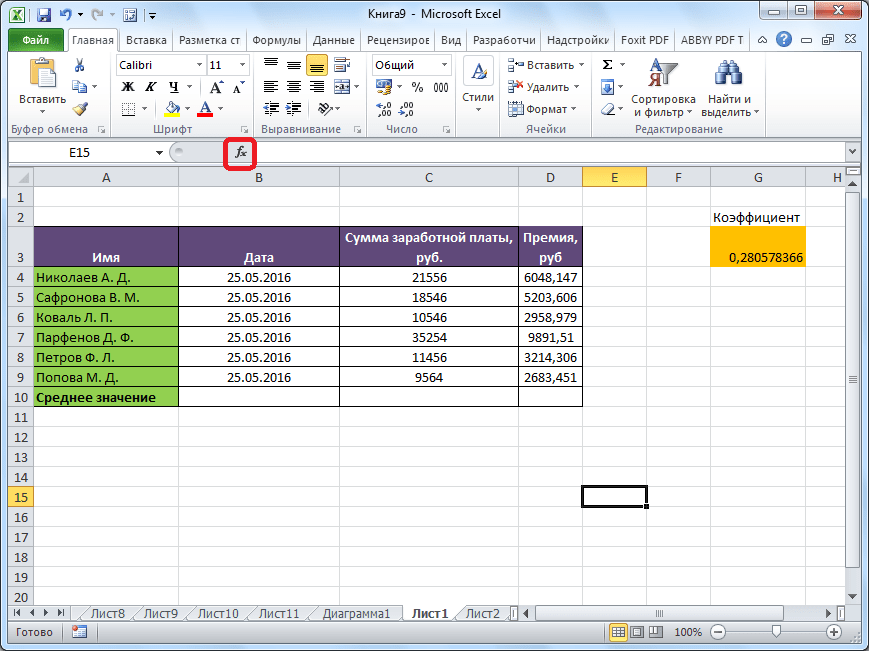
Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.
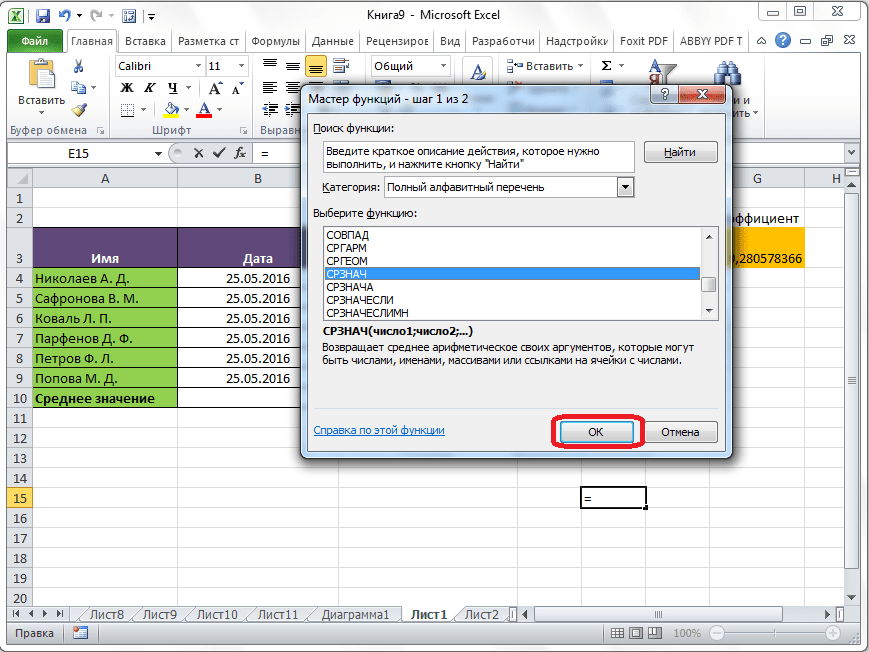
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».
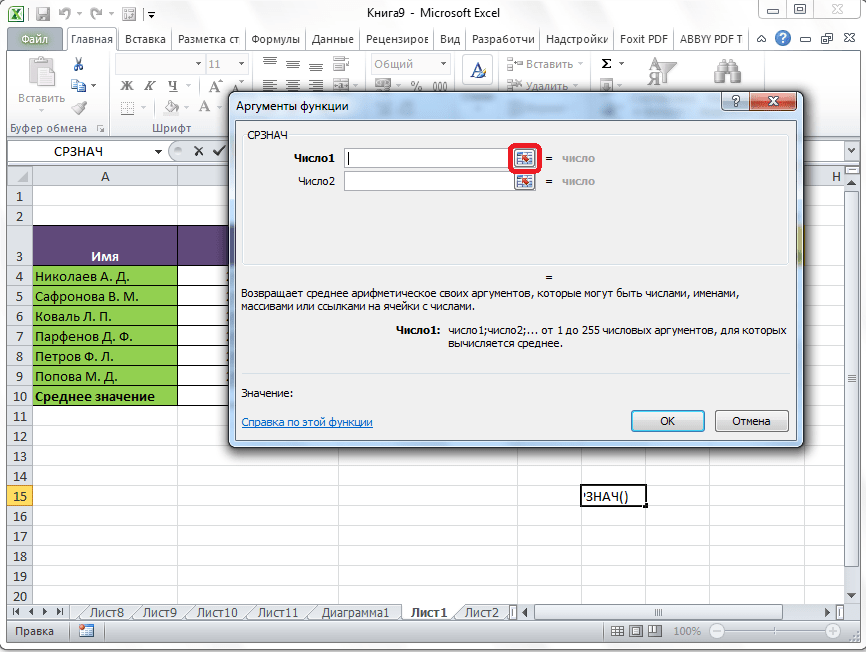
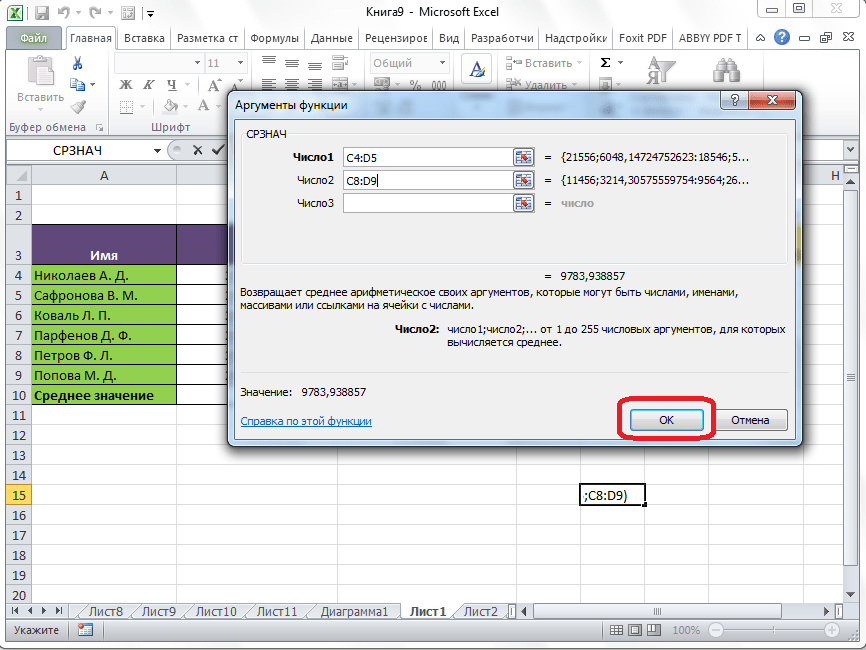
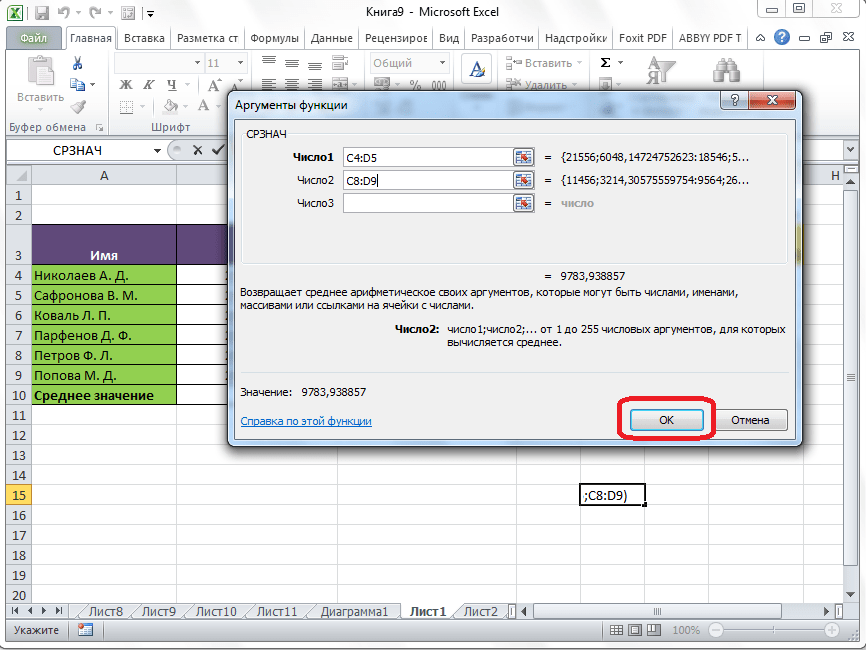
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.
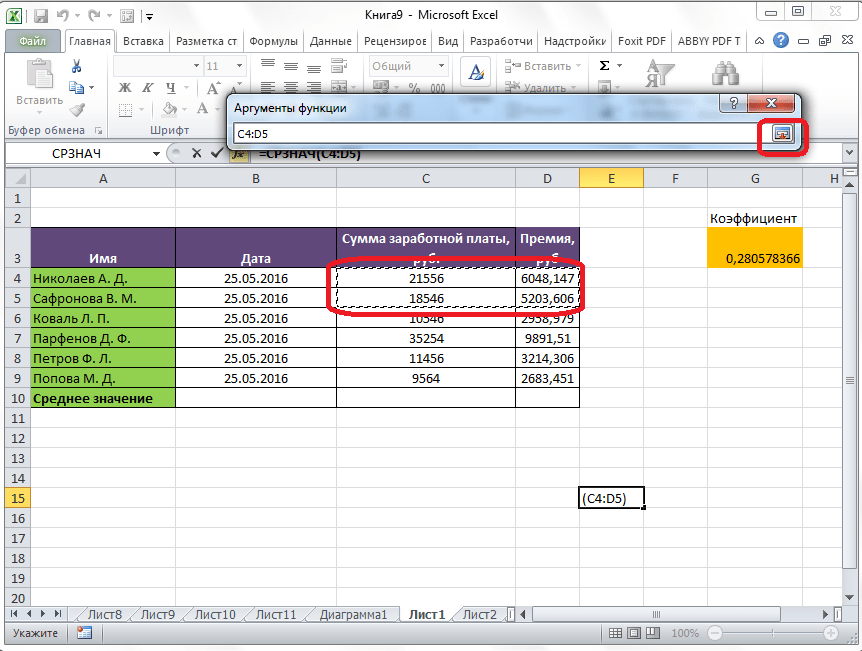
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.
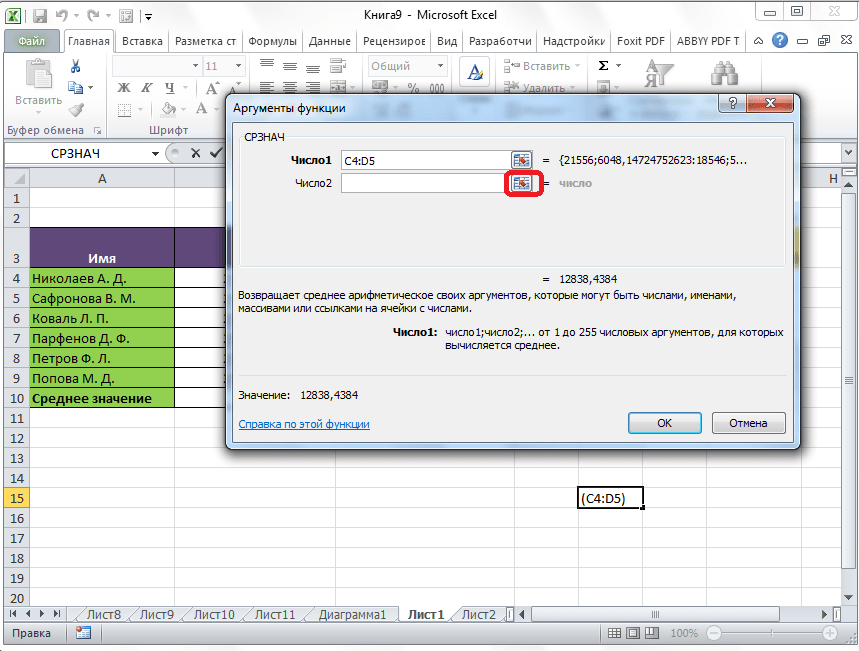
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.
После этого, жмите на кнопку «OK».
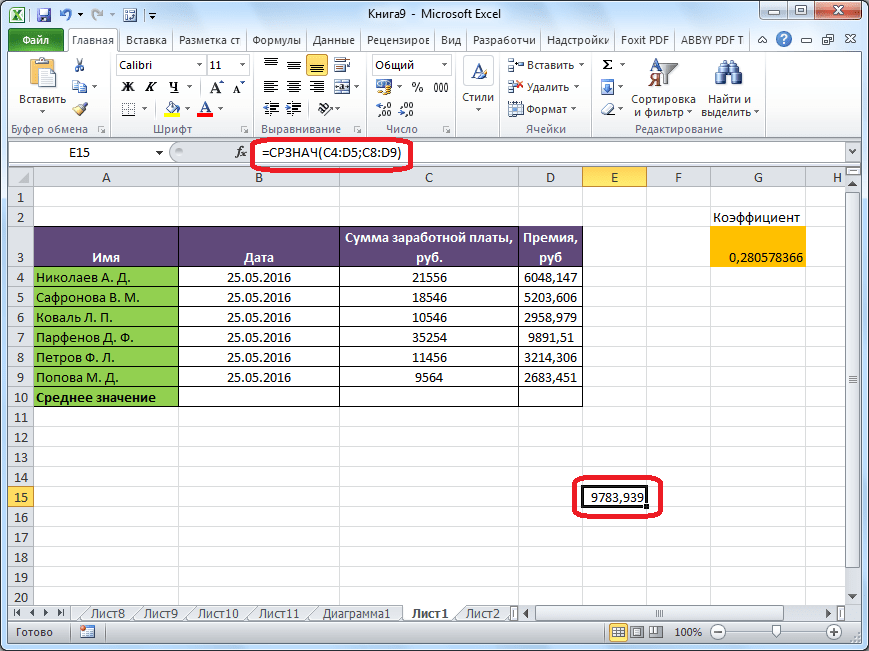
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.
Панель формул
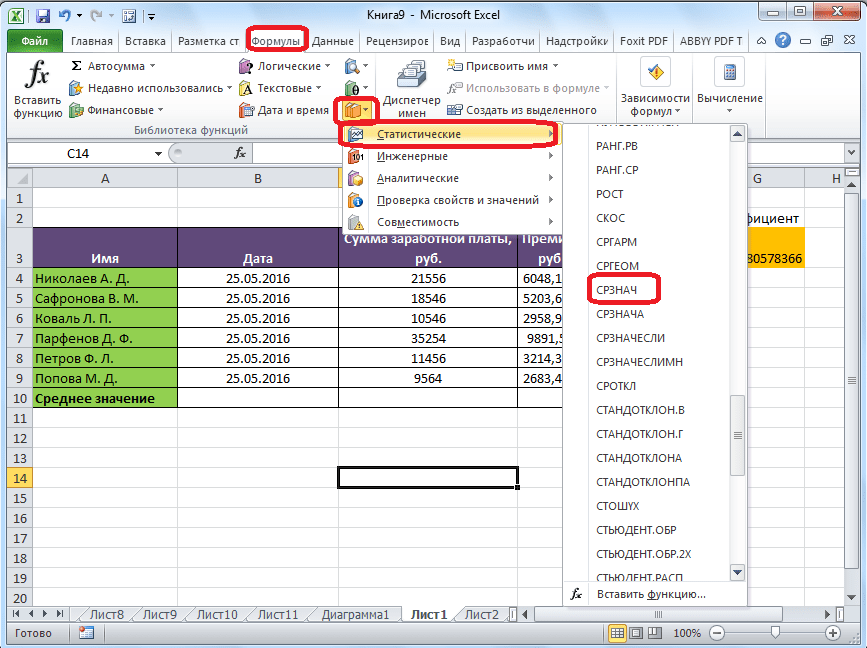
Существует ещё третий способ запустить функцию «СРЗНАЧ». Для этого, переходим во вкладку «Формулы». Выделяем ячейку, в которой будет выводиться результат. После этого, в группе инструментов «Библиотека функций» на ленте жмем на кнопку «Другие функции». Появляется список, в котором нужно последовательно перейти по пунктам «Статистические» и «СРЗНАЧ».
Затем, запускается точно такое же окно аргументов функции, как и при использовании Мастера функций, работу в котором мы подробно описали выше.
Дальнейшие действия точно такие же.
Ручной ввод функции
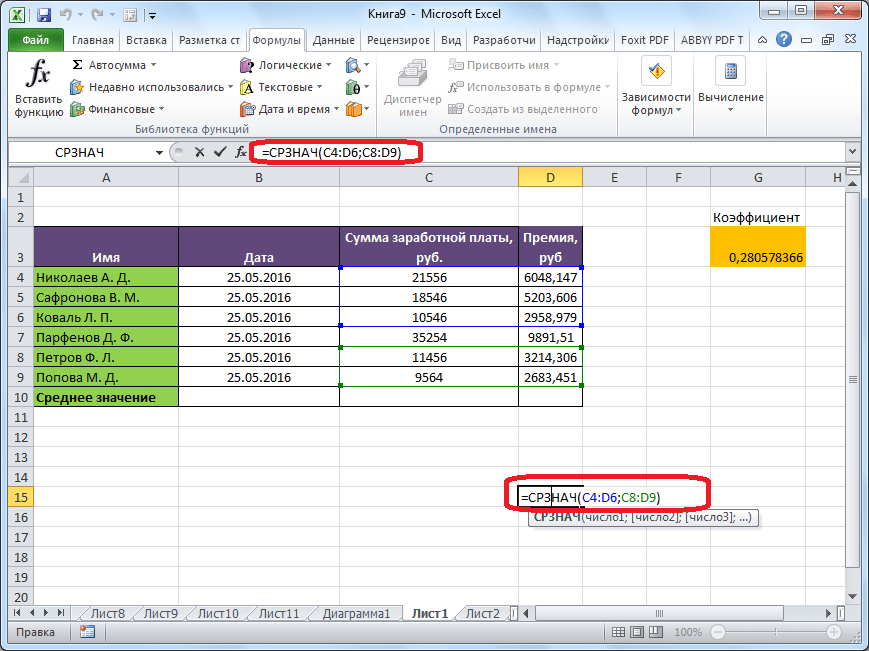
Но, не забывайте, что всегда при желании можно ввести функцию «СРЗНАЧ» вручную. Она будет иметь следующий шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
Конечно, этот способ не такой удобный, как предыдущие, и требует держать в голове пользователя определенные формулы, но он более гибкий.
Расчет среднего значения по условию
Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.
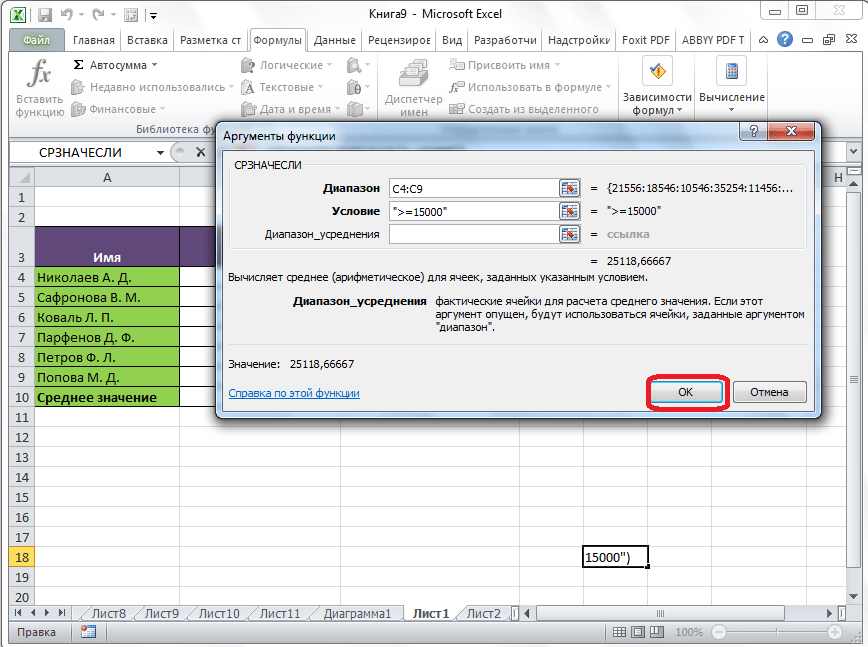
Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».
А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.
Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.
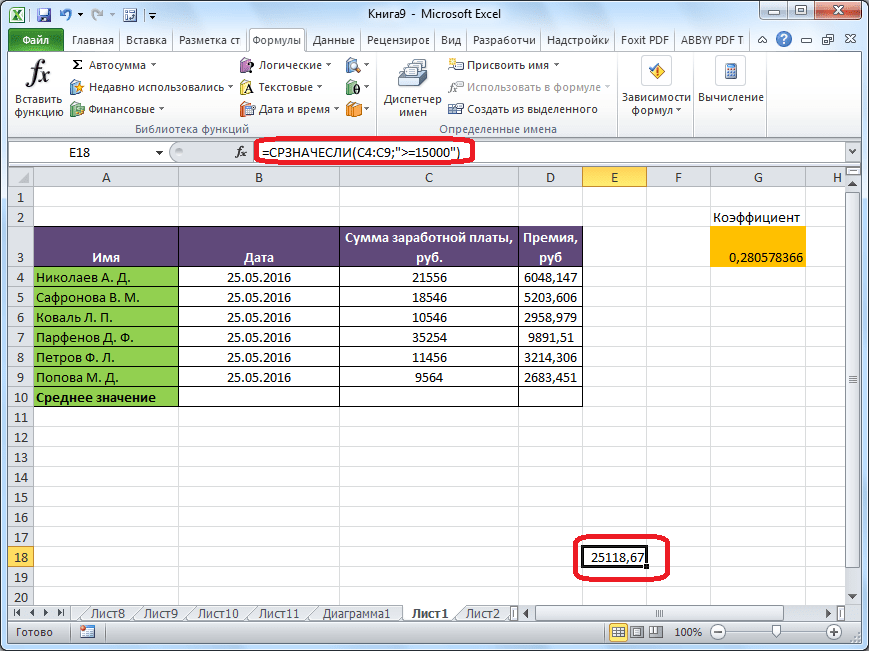
Когда все данные введены, жмем на кнопку «OK».
После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.
Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.
Помимо этой статьи, на сайте еще 12419 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Источник
Способ нахождения среднего значения
Средняя арифметическая величина выборки
характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений:
где — значение конкретного показателя,
— число показателей (случаев).
Практическое задание : рассчитать среднее арифметическое значение измерений силы кисти спортсмена по следующим результатам: 46, 50, 59, 60, 55, 49 кг.
Среднее арифметическое дает возможность:
1) охарактеризовать исследуемую совокупность одним числом;
2) сравнить отдельные величины со средним арифметическим;
3) определить тенденцию развития какого-либо явления;
4) сравнить разные совокупности;
5) вычислить другие статистические показатели, так как многие статистические вычисления опираются на среднее арифметическое.
Однако одно только среднее арифметическое не дает возможности глубоко анализировать сущность того или иного явления и их взаимные различия!
При анализе статистической совокупности одним из важных показателей является расположение значений элементов совокупности вокруг среднего значения (варьирование). Для характеристики варьирования в практике исследовательской работы рассчитывают среднее квадратическое (или стандартное) отклонение , которое отражает степень отклонения результатов от среднего значения, выражается в тех же единицах измерения.
Стандартное отклонение обозначается знаком (сигма) и вычисляется по формуле:
где — ) — сумма разности квадратов между каждым показателем и средней арифметической величиной (сумма квадратов отклонений);
— объем выборки (число измерений или испытуемых).
Если число измерений не более 30, т.е. 30, используется формула:
Порядок вычислений (1 вариант):
1. Заполнить первые две колонки таблицы расчетов (вычисление стандартного отклонения на примере показателей шести результатов измерения кистевой динамометрии).
2. Рассчитать среднюю арифметическую величину:
3. Вычислить разность между каждым показателем и данной средней (третья колонка таблицы).
4. Полученные разности возвести в квадрат и суммировать (четвертая колонка таблицы).
5. Вычислить среднее квадратическое отклонение по формуле:
Порядок вычислений (2 вариант):
Более простой способ вычисления стандартного отклонения осуществляется по следующей формуле:
где — наибольшее значение показателя; Х — наименьшее значение показателя; табличный коэффициент (табл. 3).
Чем меньше величина , тем плотнее результаты около средней, что может говорить как о стабильности показателей одного испытуемого, так и ровности результатов группы или одинаковой подготовленности спортсменов.
Выборка результатов (какой бы она не была большой) не совпадает по абсолютной величине с соответствующими генеральными параметрами. Например, результаты физической подготовленности мастеров спорта одной спортивной школы не могут точно характеризовать результаты всех мастеров спорта страны. Величина отклонения выборочной средней от ее генерального параметра называется статистической стандартной ошибкой выборочного среднего арифметического . Иногда этот показатель называется просто ошибкой средней .
Этот показатель обозначается символом и рассчитывается по формулам:
где — среднее квадратическое отклонение выборочной совокупности;
— объем выборки (число измерений или испытуемых).
Значение стандартной ошибки средней арифметической ( указывает, насколько изменится среднее значение, если его перенести на всю генеральную совокупность.
Например, при измерениях у 20 спортсменов угла в коленном суставе ноги, стоящей на задней стартовой колодке, был получен следующий результат:
Это обозначает, что полученная средняя арифметическая величина в других аналогичных исследованиях может иметь значения от до .
Практическое задание : студенты рассчитывают m среднего арифметического силы кисти руки спортсмена и делают вывод по следующим исходным данным:
Источник
Правильное среднее
Я уже много раз говорил о том, что усреднение — опасная штука. Когда цифр много, то так и хочется упростить реальность и сказать: а в среднем все так и этак. Казалось бы, ну что уж тут сложного: это плюс то делим на сё — вот тебе и среднее. И в большинстве случаев именно здесь и начинаются грубые, но совсем незаметные ошибки.
Как же нужно правильно считать среднее?
Начнем с главного: среднее — это не просто число. Это число со смыслом. Причем со вполне конкретным физическим смыслом, который мы можем (и должны) ощущать в реальном мире. Нельзя оперировать только цифрами на бумаге или в компьютере, иначе можно получить бессмысленные и нереальные цифры.
Существует много видов средних, но в каждой ситуации только одно из них правильное. Только один вид среднего следует использовать в каждом конкретном случае, и ошибка может вам стоить очень дорого.
Среднее арифметическое
Самый простой и широко известный вид среднего значения: складываем все значения, делим на количество значений — и получаем среднее арифметическое.
Именно это среднее обычно используется для усреднения всего подряд. но используется обычно неправильно.
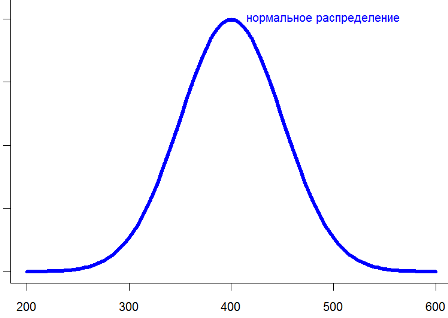
Дело в том, что в основе такого усреднения лежит закон больших чисел и допущение, что исходная величина распределена нормально. А это подразумевает, что возможные значения сконцентрированы вокруг некоторого наиболее частого значения, а отклонения и в большую, и в меньшую сторону относительно невелики и равновероятны.
Проблема в том, что в бизнесе нормальное распределение встречается довольно редко .
Длительность обслуживания, длина очередей, время ожидания, сумма контракта, размер перевода, остатки на счетах, доля рынка, процент прироста — все эти и многие другие бизнес-показатели распределены не нормально, и их, как правило, не стоит усреднять с помощью средего арифметического.
Нормальное распределение обычно встречается при большом числе значений — сотни и тысячи штук. Например, число обращений в крупный колл-центр может быть распределено нормально. Однако одного количества мало, и поэтому в каждом случае следует убедиться в нормальности распределения, чтобы без сомнений усреднять с помощью среднего арифметического.
В следующих записях я приведу интересные примеры неправильного усреднения, а сейчас перейдем к другим видам среднего.
Среднее гармоническое
Первые 100 км автомобиль проехал со скоростью 50 км/ч, а следующие 100 км — со скоростью 80 км/ч. С какой средней скоростью двигался автомобиль на всем пути?
Сначала, наверное, может показаться, что правильное значение 65 км/ч, потому что (50+80)/2 = 65.
Однако быстро становится понятно, что если бы другой автомобиль двигался со средней скоростью, то он провел бы в пути столько же времени, что и первый. Именно в этом смысл усреднения в данном случае.
И вот тут на помощь приходит среднее гармоническое:
Для нашей задачи искомое среднее равно 2/(1/50+1/80)=61.54 км/ч. И действительно в первом случае автомобиль затратил 2 часа на преодоление 100 км со скоростью 50 км/ч и еще 1.25 часа ему потребовалось на следующие 100 км, потому что скорость возросла до 80 км/ч. Таким образом, всего ушло 3.25 часа.
Если бы автомобиль все 200 км двигался со скоростью 61.54 км/ч, то у него также ушло бы на дорогу 3.25 часа.
Близость значений 65 и 61.54 не должна вас обманывать. Среднее гармоническое в данном случае не просто дает более точный результат. Это единственно правильный способ усреднения , потому что он соответствует физическому смыслу измеряемых явлений.
При других исходных данных разница между средним гармоническим и средним арифметическим могла бы быть больше. Но среднее арифметическое здесь не имеет никакого смысла. Для усреднения в подобных задачах допустимо использовать только среднее гармоническое.
Обычно задачи этого типа связаны со временем и производительностью: например, сотрудник А выполняет операцию за 10 минут, а сотрудник Б — за 25 минут; сколько в среднем им требуется времени на выполнение операции, если бы они работали вместе?
Правильный ответ: 14 мин 17 сек. А отличие от среднего арифметического (17 мин 30 сек) уже превышает 20%. Именно на столько вы бы ошиблись, если бы усредняли неправильно.
Среднее геометрическое
В 2009 году выручка выросла на 12% от уровня 2008 года, а в в 2010 — на 42% от уровня 2009. На сколько росла выручка в среднем за год?
Можно предположить, что есть несколько вариантов усреднения. Во-первых, среднее арифметическое: (12+42)/2 = 27%. Во-вторых, сложный процент: 1.12*1.42=1.5904, т.е. 59.04% за 2 года или 28.02% за год.
Но «в среднем» означает, что применив это значение к каждому году, мы получим тот же самый результат, что и при использовании множества исходных значений.
Проверяем. Среднее арифметическое: 1.27*1.27=1.6129 (на 61.29%). Сложный процент: 1.2802*1.2802=1.6389 (на 63.89%). Результаты мало того, что разные, так и оба неправильные, потому что выручка за 2 года выросла на 59.04%.
В данном случае есть только один осмысленный способ усреднения — это среднее геометрическое
Таким образом, для нашей задачи средний прирост за год составит 26.11% (проверка 1.2611*1.2611=1.5904)
Среднее геометрическое часто встречается в реальных бизнес-задачах вместе с процентами и долями. Если в вашей задаче что-то растет или падает и вы хотите усреднить динамику показателя, то вам следует применять среднее геометрическое.
Вместо заключения
Повторю главные моменты:
— среднее арифметическое далеко не всегда соответствует смыслу и физической сущности усредняемого показателя;
— существует много видов средних значений, но в каждом конкретном случае есть только один правильный вид среднего, и именно его следует использовать в расчетах.
Источник