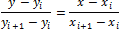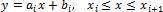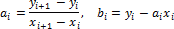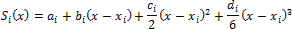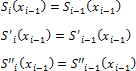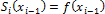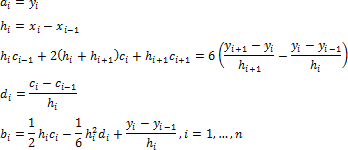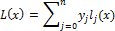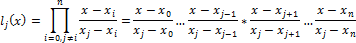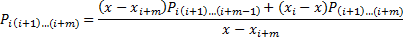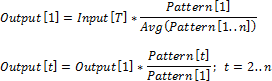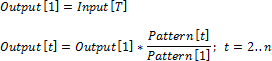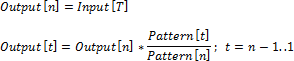Способ нахождения промежуточных значений методом интерполяции

Определение промежуточного значения методом линейной интерполяции

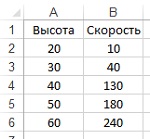
Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.

Рис. 1. Высота над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр)

Скачать заметку в формате Word или pdf, примеры в формате Excel

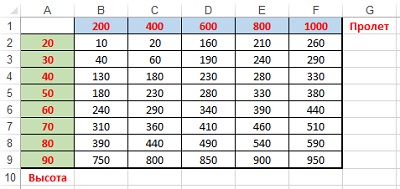
Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций. Требуется вычислить давление ветра на высоте 25 метров и величине пролета 300 метров.

Рис. 2. Исходная таблица для интерполяции по двум управляющим параметрам

Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.

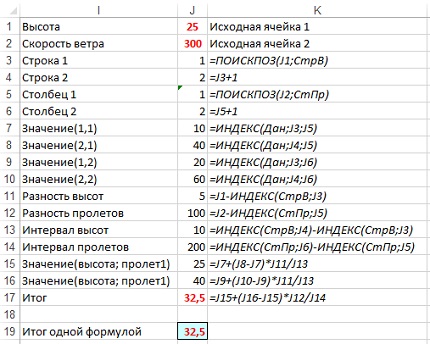
Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).

Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы

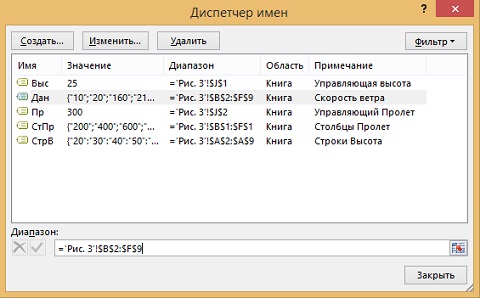
Для удобства использования формул определите имена (рис. 4).

Рис. 4. Определенные имена

Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.

Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.

Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.

Источник

Интерполяция

Интерполяция — это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Интерполяция использует значения некоторой функции, заданные в ряде точек, чтобы предсказать значения функции между ними. Перечисленные ниже методы предназначены для создания ряда с более высокой частотой наблюдений на основе ряда с низкой частотой. Например, вычислить ряд с квартальной динамикой на основе ряда годовых данных.

Предположим, что есть система несовпадающих точек x i ( i ϵ 0, 1, …, N ) из некоторой области G . Значения функции f известны только в этих точках: y i = f ( x i ), i = 1, …, N .

Процесс интерполяции состоит в поиске такой функции f из заданного класса функций, что F ( x i ) = y i , i = 1, …, N .

Точки x i являются узлами интерполяции, а их совокупность — интерполяционной сеткой.

Пары ( x i , y i ) являются точками данных (базовыми точками).

Разность между «соседними» значениями ∆ x i = x i — x i — 1 — называют шагом интерполяционной сетки. Шаг может быть переменным или постоянным.

Функцию F ( x ) — интерполирующей функцией (интерполянтой).

Линейная интерполяция

При линейной интерполяции существующие точки данных М ( x i , y i ) ( i = 0, 1, . n ) соединяются прямыми линиями и функция f ( x ) приближается к ломаной с вершинами в данных точках.

Уравнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов ( x i , x i+1 ), то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности, для i -го интервала можно написать уравнение прямой, проходящей через точки ( x i , y i ) и ( x i+1 , y i+1 ), в виде:

Геометрическая интерполяция

При геометрической интерполяции значения результирующей динамики пропорциональны значению инкремента и обратно пропорциональны фактору, вычисленному на основе инкремента. Инкремент экспоненциально зависит от логарифма относительного прироста исходной динамики, умноженного на длину периода результирующей динамики.

Рассмотрим принцип геометрического метода на примере вычисления квартальных данных на основе годовых.

X [ t ] – исходные данные по годам;

Factor [ t ] = (1 + Inc [ t ] + Inc [ t ]^2 + Inc [ t ]^3) / 4 – значение фактора;

Из этого следует:

Интерполяция для других динамик осуществляется аналогичным образом.

Интерполяция кубическими сплайнами

Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющих достаточно сложную структуру. Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны. Основные идеи теории кубических сплайнов сформировались в результате попыток математически описать гибкие рейки из упругого материала (механические сплайны), которыми издавна пользовались чертежники в тех случаях, когда возникала необходимость проведения через заданные точки достаточно гладкой кривой. Известно, что рейка из упругого материала, закрепленная в некоторых точках и находящаяся в положении равновесия, принимает форму, при которой ее энергия является минимальной. Это фундаментальное свойство позволяет эффективно использовать сплайны при решении практических задач обработки экспериментальной информации.

В общем случае для функции y = f ( x ) требуется найти приближение y = ϕ( x) таким образом, чтобы f ( x i ) = ϕ( x i ) в точках x = x i , а в остальных точках отрезка [a, b] значения функций f ( x ) и ϕ( x) были близкими между собой. При малом числе экспериментальных точек (например, 6-8) для решения задачи интерполяции можно использовать один из методов построения интерполяционных полиномов. Однако при большом числе узлов интерполяционные полиномы становятся практически непригодными. Это связано с тем, что степень интерполяционного полинома лишь на единицу меньше числа экспериментальных значений функций. Можно, конечно, отрезок, на котором определена функция, разбить на участки, содержащие малое число экспериментальных точек, и для каждого из них построить интерполяционные полиномы. Однако в этом случае аппроксимирующая функция будет иметь точки, где производная не является непрерывной, т.е. график функции будет содержать точки «излома».

Кубические сплайны лишены этого недостатка. Исследования теории балок показали, что гибкая тонкая балка между двумя узлами достаточно хорошо описывается кубическим полиномом, и поскольку она не разрушается, то аппроксимирующая функция должна быть, по меньшей мере, непрерывно дифференцируемой. Это означает, что функции ϕ( x) , ϕ'( x) , ϕ»( x ) должны быть непрерывными на отрезке [a, b].

Кубическим интерполяционным сплайном, соответствующим данной функции f ( x ) и данным узлам x i , называется функция S ( x ), удовлетворяющая следующим условиям:

на каждом сегменте [ x i -1 , x i ], i = 1, 2, . n функция S ( x ) является полиномом третьей степени;

функция S ( x ), а также ее первая и вторая производные непрерывны на отрезке [a, b];

На каждом из отрезков [ x i -1 , x i ], i = 0, 1, . n находится функция S ( x ) = S i ( x ) в виде полинома третьей степени:

Условие непрерывности всех производных до второго порядка записываются в виде:

a i , b i , c i , d i — коэффициенты сплайна, подлежащие определению на всех n элементарных отрезках:

Если функция f ( x ) является полиномом третьей или меньше степени, данные воспроизводятся более точно, если граничные условия сплайна c 0 и c n равны точным значениям второй производной кубического полинома.

Интерполяция многочленом Лагранжа

Интерполяционный многочлен Лагранжа — это многочлен минимальной степени, который принимает данные значения в данном наборе точек. Для n + 1 пар чисел ( x 0 , y 0 ), ( x 1 , y 1 ), …, ( x n , y n ), где все x i различны ( i = 0, 1, . n ), существует единственный многочлен L ( x ) степени не более n , для которого L ( x i ) = y i .

В самом простом случае ( n = 1) — это линейный многочлен и его график — прямая, проходящая через две заданные точки.

Лагранж предложил методику вычисления подобных многочленов:

Где базисные полиномы определяются по следующей формуле:

l j ( x ) обладают свойствами:

являются многочленами степени n ;

Из этого следует, что L ( x ), как линейная комбинация l j ( x ), может иметь степень не больше n , и L ( x j ) = y j .

Полиноминальная интерполяция

Полиномиальная интерполяция является наиболее известным из методов одномерной интерполяции. Её достоинствами являются простота реализации и хорошее качество получаемых интерполянтов.

Данный метод представляет полином n -ой степени P 0, 1, …, n -1, n , проходящий через n точек (с 0-ой по n -ую), как функцию двух полиномов n -1-ой степени по формуле:

К полученным полиномам рекурсивно применяется та же формула, до тех пор, пока мы не дойдем до полиномов вида P i , которые вычисляются по формуле P i = y i .

Достоинством данного метода является простота реализации, недостатком — сравнительно невысокое быстродействие.

Равномерная интерполяция

Значение исходного ряда делится на число наблюдений, попадающих в один период результирующего ряда. Полученное значение присваивается всем наблюдениям нового ряда, в пределах одного периода.

Повторная интерполяция

Значения исходного ряда повторяются на всех наблюдениях ряда с более высокой частотой динамики.

Интерполяция по шаблону

Пусть Input — входной ряд, Output — выходной ряд, Pattern — шаблонный ряд. Обозначим за t текущую дату входного ряда, а за n — количество точек выходного ряда в одном периоде.

Рассмотрим три метода интерполяции по шаблону:

среднее по элементам

по первому элементу

по последнему элементу

Первое значение

Значение первой точки результирующей динамики будет совпадать со значением точки на исходной динамике. Значения в остальных точках результирующей динамики остаются пустыми.

Последнее значение

Значение последней точки результирующей динамики будет совпадать со значением точки на исходной динамике. Значения в остальных точках результирующей динамики остаются пустыми.

Источник

Интерполяция данных: соединяем точки так, чтобы было красиво

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P₁&nbsp. &nbspP_n, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n&nbsp–&nbsp1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции f_i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P_i) называется сплайном.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Ставим опыты

Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

Результат линейной интерполяции этих точек выглядит так:

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a;&nbspb], это означает, что на [a;&nbspb] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n&nbsp–&nbsp1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k&nbsp+&nbsp1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k&nbsp–&nbsp1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k&nbsp=&nbsp1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k&nbsp–&nbsp1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k&nbsp=&nbsp3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P_i), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

В качестве прямых, на которых лежат точки C_{i&nbsp–&nbsp1} (2) , P_i и C_i (1) , целесообразно взять касательные к графику интерполируемой функции в точках P_i. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C₁ (1) и C_{n&nbsp–&nbsp1} (2) совпадают с точками P₁ и P_n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P_i до точек C_{i&nbsp–&nbsp1} (2) и C_i (1) , но при этом сохраняем их все лежащими на одной прямой:

Эвристика для вычисления расстояний будет такой:

Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Результат следующий:

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.

А как люди-то делают?

Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n&nbsp–&nbsp1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Источник