Пределы числовых последовательностей
Содержание
 Предел числовой последовательности |
| Свойства пределов числовых последовательностей |
| Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии |
| Примеры вычисления пределов последовательностей. Раскрытие неопределенностей |
| Число e. Второй замечательный предел |
Предел числовой последовательности
ОПРЕДЕЛЕНИЕ 1 . Число a называют пределом числовой последовательности
если для любого положительного числа ε найдется такое натуральное число N , что при всех n > N выполняется неравенство
записывают с помощью обозначения
и произносят так: «Предел an при n , стремящемся к бесконечности, равен a ».
То же самое соотношение можно записать следующим образом:
an → a при 
.
Словами это произносится так: « an стремится к a при n , стремящемся к бесконечности».
ЗАМЕЧАНИЕ . Если для последовательности
найдется такое число a , что an → a при , то эта последовательность ограничена.
ОПРЕДЕЛЕНИЕ 2 . Говорят, что последовательность
стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N , что при всех n > N выполняется неравенство
Условие того, что числовая последовательность
стремится к бесконечности, записывают с помощью обозначения
или с помощью обозначения
при .
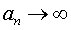
ПРИМЕР 1 . Для любого числа k > 0 справедливо равенство
ПРИМЕР 2 . Для любого числа k > 0 справедливо равенство
ПРИМЕР 3 . Для любого числа a такого, что | a | справедливо равенство
ПРИМЕР 4 . Для любого числа a такого, что | a | > 1, справедливо равенство
ПРИМЕР 5 . Последовательность
предела не имеет.
Свойства пределов числовых последовательностей
Рассмотрим две последовательности
Если при существуют такие числа a и b , что
и 
,
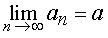
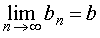
то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем
| ||||||||
|
| |||||||
|
Если, кроме того, выполнено условие
то при
Для любой непрерывной функции f (x) справедливо равенство
Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессиизнаменатель которой равен q . Для суммы первых n членов геометрической прогрессии
Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение то будет справедлива формула
В случае бесконечно убывающей геометрической прогрессии знаменатель q удовлетворяет неравенству | q | ОПРЕДЕЛЕНИЕ 3 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к Часто неопределенность типа ПРИМЕР 6 . Найти предел последовательности
РЕШЕНИЕ . Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 3, получаем
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и сокращая дробь, получаем
ОТВЕТ . ПРИМЕР 7 . Найти предел последовательности
РЕШЕНИЕ . Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
РЕШЕНИЕ . Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби:
ОТВЕТ . В следующих двух примерах показано, как можно раскрыть неопределенности типа ПРИМЕР 8 . Найти предел последовательности
РЕШЕНИЕ . Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:
ОТВЕТ . ПРИМЕР 9 . Найти предел последовательности
РЕШЕНИЕ . В рассматриваемом примере неопределенность типа
Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а затем сокращая дробь на n 2 :
ОТВЕТ . ПРИМЕР 10 . Найти предел последовательности
РЕШЕНИЕ . Замечая, что для всех k = 2, 3, 4, … выполнено равенство
Число e. Второй замечательный предел
В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой e . Таким образом, справедливо равенство
причем расчеты показывают, что число Число e играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции которую называют «экспонента».
что позволяет вычислять число e с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики. ЗАМЕЧАНИЕ . Предел (2), в котором для последовательностей раскрывается неопределенность типа Источник |
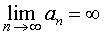
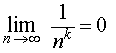
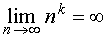
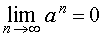
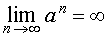
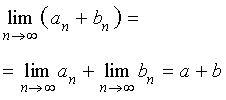
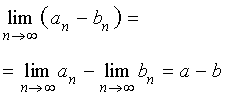
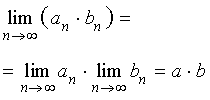
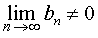
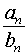
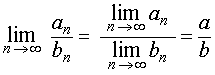
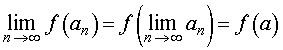
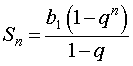
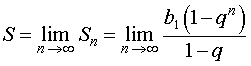
, то вычисление такого предела называют раскрытием неопределенности типа 
.
.
,
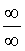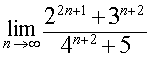
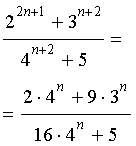
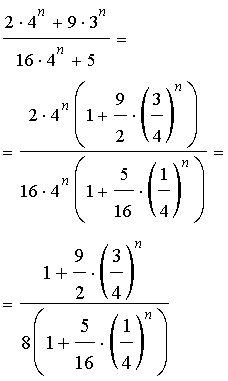
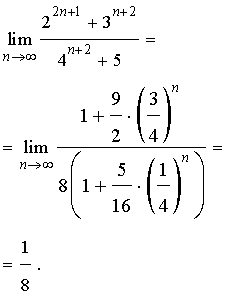
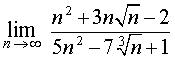
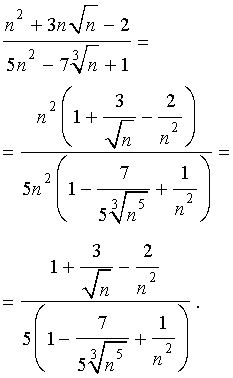
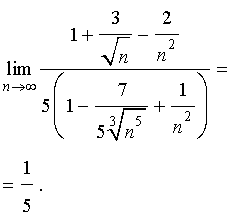
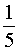
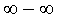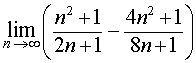
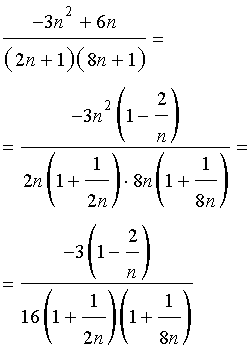
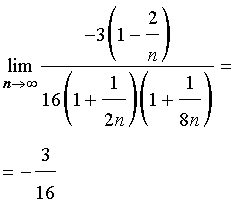
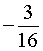
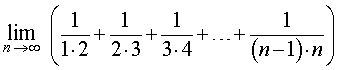
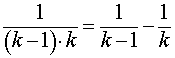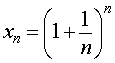
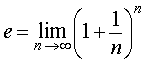
, называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.
