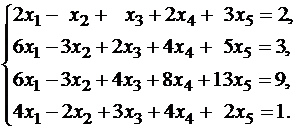Способ нахождения общего решения одно

Как найти общее решение однородного дифференциального уравнения

Данный тип задачи часто ставит студентов в тупик. Поэтому они присылают их на решение к нам. Мы написали данную статью, чтобы помочь разобраться в этой теме. Итак, прежде, чем приступать решать дифференциальное уравнение, необходимо понять к какому виду оно принадлежит. Сначала определить порядок, затем уже линейность и однородность. В данном материале рассмотрим однородные уравнения первого и второго порядка и как их решать. В зависимости от этого будет разный алгоритм действий. Так как в первом случае однородность уравнения по переменным, а во втором по правой части. Далее разберемся подробнее об этом.

Однородные ДУ первого порядка

Если после подстановки в уравнение вместо $x$ и $y$ соответствующих $\lambda x$ и $\lambda y$ можно добиться уничтожения всех $\lambda$, то уравнение является однородным первого порядка.

Такие уравнения имеют общий вид $$P(x,y)dx+Q(x,y)dy=0,$$ где $P(x,y)$ и $Q(x,y)$ однородные функции одинакового порядка, то есть выполняются условия $P(\lambda x,\lambda y) = \lambda^n P(x,y)$ и $Q(\lambda x,\lambda y) = \lambda^n Q(x,y)$.

1. Проверить уравнение на однородность с помощью $\lambda$
2. Привести уравнение к виду $y’ = f(\frac)$
3. Выполнить замену $\frac= t$ и $y’ = t’x+t$
4. Решить уравнение методом разделяющихся переменных.

Подставляя $\lambda$ перед $x$ и $y$ в исходное уравнение получаем $$y’ = e^\frac<\lambda y> <\lambda x>+ \frac<\lambda y><\lambda x>,$$ в котором все $\lambda$ сокращаются, и это означает, что перед нами однородное дифференциальное уравнение первого порядка.

Выполняем замену $\frac = t \Rightarrow y’ = t’x + t$ в исходном уравнении и получаем: $$t’x+t=e^t+t$$ $$t’x=e^t.$$ Данное уравнение с разделяющимися переменными. Записываем его соответствующим образом и переносим всё, что содержит $t$ в левую часть, а то что с $x$ в правую: $$\frac

x=e^t$$ $$\frac

=\frac.$$ Интегрируем обе части уравнения: $$\int \frac

=\int \frac$$ $$-e^ <-t>= \ln|x|+C.$$

Теперь необходимо выполнить обратную замену $t = \frac$, чтобы вернуться к $y$ $$-e^<-\frac> = \ln|x| + C.$$ Записываем ответ в виде общего интеграла $$e^<-\frac>+\ln|x|=C.$$

Пример 1

Решить однородное дифференциальное уравнение первого порядка $$y’=e^\frac+\frac.$$

Решение

Ответ

$$e^<-\frac>+\ln|x|=C$$

Подставляем перед всеми иксами и игриками дополнительную константу $\lambda$, чтобы убедиться в однородности уравнения: $$( (\lambda x)^2 + 2\lambda x \lambda y)d(\lambda x) + \lambda x \lambda y d(\lambda y) = 0$$ $$\lambda^3 (x^2+2xy)dx+\lambda^3 xydy = 0$$ $$(x^2+2xy)dx+xydy=0.$$ Как видно, все $\lambda$ уничтожились, поэтому действительно дано однородное ДУ первого порядка.

Приведем уравнение к виду $y’ = f(\frac)$. Разделим уравнение на $x^2$ и $dx$. Получим $$(1+2\frac)+\frac\frac = 0.$$ Теперь выполняем замену $$\frac=t, \qquad \frac = t’x+t.$$ Подставляем это в уравнение и получаем $$(1+2t)+t(t’x+t) = 0, $$ и раскрываем скобки и упрощаем: $$1+2t+t’tx+t^2=0$$ $$t’tx + (t+1)^2=0.$$

Получившееся уравнение является ДУ с разделяющимися переменными. Поэтому начинаем резделять переменные $t$ и $x$ по разные стороны от знака равенства. Записываем уравнение в виде $$\frac

tx = -(t+1)^2.$$ Делим обе части на $(t+1)^2$ и $x$, затем умножаем на $dx$ $$\frac <(t+1)^2>= -\frac.$$

Последнее равенство нужно проинтегрировать, чтобы вытащить $t(x)$ $$\int \frac <(t+1)^2>= — \int \frac.$$ Решаем первый интеграл методом разложения: $$\int \frac <(t+1)^2>= \int \frac<(t+1)-1><(t+1)^2>dt = \int \frac<(t+1)^2>dt — \int \frac

<(t+1)^2>= $$ $$ = \int \frac

— \int \frac

<(t+1)^2>= $$ $$ = \ln|t+1| + \frac<1> + C.$$ Решаем второй интеграл $$\int \frac = \ln|x| + C.$$ Возвращаемся к равенству двух интегралов и подставляем полученные решения $$\ln|t+1| + \frac<1> = -\ln|x|+C.$$

Вспоминаем, что в начале решения задачи была сделана подстановка $\frac=t$, и значит, назад нужно вернуться к $y$ $$\ln|\frac+1|+\frac<1><\frac+1> = -\ln|x| + C.$$ Выполняем преобразования последнего уравнения: $$\ln|\frac|+\frac=-\ln|x|+C$$ $$\ln|x+y|-\ln|x|+\frac=-\ln|x|+C$$ $$\ln|x+y|+\frac=C.$$ Выразить $y$ просто так не получится. Поэтому оставим ответ в таком виде, который называется общий интеграл дифференциального уравнения.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Пример 2

Найти решение однородного дифференциального уравнения первого порядка $$(x^2+2xy)dx+xydy=0.$$

Решение

Ответ

$$\ln|x+y|+\frac=C$$

Как всегда начинает с проверки на однородность с помощью подстановки $\lambda$ в исходное ДУ $$\lambda xy’ \sin\frac<\lambda y><\lambda x>+\lambda x=\lambda y\sin \frac<\lambda y><\lambda x>.$$ Видим, что все $\lambda$ сокращаются и уравнение приобретает вид из условия задачи. Значит, это однородное ДУ первого порядка.

Придадим ему вид $y’=f(\frac)$ для удобства замены. Для этого разделим обе части уравнения на $x$ $$y’ \sin\frac+1=\frac \sin \frac.$$ Теперь делаем подстановку $\frac=t$ и $y’=t’x+t$: $$(t’x+t) \sin t + 1 = t \sin t$$ $$t’x \sin t + t\sin t+1=t\sin t$$ $$t’x \sin t=-1.$$ Получили уравнение с разделяющимися переменными. Всё, что с $t$ налево, всё что с $x$ направо: $$\frac

x \sin t = -1$$ $$\sin t dt = -\frac.$$

Интегрируем обе части равенства: $$\int \sin t dt = -\int \frac$$ $$-\cos t = -\ln|x|+C.$$ Выполняем обратную замену в последнем уравнении $$\cos \frac = \ln|x|+C.$$ Так как выразить $y$ достаточно тяжело, то запишем ответ в виде общего интеграла $$\cos \frac-\ln|x|=C.$$

Пример 3

Решить однородное дифференциальное уравнение $$xy’ \sin\frac+x=y\sin \frac.$$

Решение

Ответ

$$\cos \frac-\ln|x|=C$$

Однородные линейные ДУ второго порядка с постоянными коэффициентами

Такие уравнения имеют следующий общий вид $$y»+py’+qy=0, $$ где $p$ и $q$ постоянные коэффициенты. Чтобы решить такие уравнения первым делом нужно составить характеристический многочлен $$\lambda^2+p\lambda + q = 0, $$ который получается путем замены всех $y$ на $\lambda$ в степенях, соответствующих порядку производной $y$ $$y» \Rightarrow \lambda^2, \quad y’ \Rightarrow \lambda, \quad y \Rightarrow 1.$$ Затем в зависимости от найденных корней $\lambda_1$ и $\lambda_2$ составляется общее решение:

1. Если $\lambda_1 \neq \lambda_2$, тогда $y=C_1e^x + C_2e^x$
2. Если $\lambda_1 = \lambda_2$, тогда $y=C_1e^x + C_2xe^x$
3. Если $\lambda_ <1,2>= \alpha \pm \beta i$, тогда $y=C_1e^ <\alpha x>\cos \beta x + C_2 e^ <\alpha x>\sin \beta x$.

Составляем характеристический многочлен путем замены $y$ на $\lambda$ в степени, соответствующей порядку производной и находим его корни: $$\lambda^2 — 9 = 0$$ $$(\lambda — 3)(\lambda+3)=0$$ $$\lambda_1=3, \quad \lambda_2=-3.$$

Так как получили действительные корни, отличающиеся друг от друга, то общее решение однородного уравнения будет выглядеть следующим образом $$y=C_1e^<-3x>+C_2e^<3x>.$$

Источник

Как найти общее и частное решение системы линейных уравнений

Пример 2. Исследовать совместность, найти общее и одно частное решение системы

Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.

Получим нули в четвертом столбце, оперируя первой строкой:

Теперь получим нули в третьем столбце с помощью второй строки:

Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:

Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x₁=-3 → x₁=3; x₂=3-x₁ → x₂=0; x₃=1-2x₁ → x₃=5.
x₄ = 10- 3x₁ – 3x₂ – 2x₃ = 11.

Пример 3. Исследовать систему на совместность и найти решение, если оно существует.

Решение. Составляем расширенную матрицу системы.

Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:

Умножим вторую строку на (-2) и прибавим к третьей:

Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r_B > r_A.

Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение

Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.

Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x₃ = — 1 + x₄ + x₅; x₂ = 1 — x₄; x₁ = 2 + x₄ — 3x₅

Задание. Найти общее и частное решения каждой системы.
Решение. Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:

Пример 4

найти общее решение однородного дифференциального уравнения второго порядка $$y»-9y=0.$$

Решение

1	1	14	0	2	0
3	4	2	3	0	1
2	3	-3	3	-2	1
x1	x2	x3	x4	x5

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	-1	40	-3	6	-1
3	4	2	3	0	1
2	3	-3	3	-2	1

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:

0	-1	40	-3	6	-1
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	0	27	0	0	0
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂,x₃, значит, неизвестные x₁,x₂,x₃ – зависимые (базисные), а x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	0	27	0	0	0
0	-1	13	-1	3	-6
2	3	-3	1	-3	2
x1	x2	x3	x4	x5

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x₃ =
— x₂ + 13x₃ = — 1 + 3x₄ — 6x₅
2x₁ + 3x₂ — 3x₃ = 1 — 3x₄ + 2x₅
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x₁,x₂,x₃ через свободные x₄,x₅, то есть нашли общее решение:
x₃ = 0
x₂ = 1 — 3x₄ + 6x₅
x₁ = — 1 + 3x₄ — 8x₅
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

Задание. Решить систему уравнений.
Ответ😡₂ = 2 — 1.67x₃ + 0.67x₄
x₁ = 5 — 3.67x₃ + 0.67x₄
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной

Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера — Капелли. Согласно теореме Кронекера — Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение

Источник