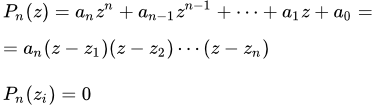Способ нахождения корней многочлена

Алгоритм расчёта вещественных корней полиномов

Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

А теперь по порядку.

Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.

Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.

Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.

В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.

Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.

Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.

Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.

Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.

Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.

Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+. +k[1]*x+k[0] по схеме Горнера.

На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.

Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.

Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.

Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.

Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt =vg)break;.

В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.

Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.

Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.

Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.

Литература

1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты

Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1

Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:

Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.

Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

Источник

Методы разложения многочленов на множители

Основа метода

Пусть

– многочлен степени n ≥ 1 от действительной или комплексной переменной z с действительными или комплексными коэффициентами a_i . Примем без доказательства следующую теорему.

Теорема 1

Уравнение P_n ( z ) = 0 имеет хотя бы один корень.

Докажем следующую лемму.

Лемма 1

Пусть P_n ( z ) – многочлен степени n , z ₁ – корень уравнения:
P_n ( z ₁) = 0 .
Тогда P_n ( z ) можно представить единственным способом в виде:
P_n ( z ) = ( z – z ₁) P_{n– 1} ( z ) ,
где P_{n– 1} ( z ) – многочлен степени n – 1 .

Доказательство

Для доказательства, применим теорему (см. Деление и умножение многочлена на многочлен уголком и столбиком), согласно которой для любых двух многочленов P_n ( z ) и Q_k ( z ) , степеней n и k , причем n ≥ k , существует единственное представление в виде:
P_n ( z ) = P_n–k ( z ) Q_k ( z ) + U_{k– 1} ( z ) ,
где P_n–k ( z ) – многочлен степени n–k , U_{k– 1} ( z ) – многочлен степени не выше k– 1 .

Положим k = 1 , Q_k ( z ) = z – z ₁ , тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) + c ,
где c – постоянная. Подставим сюда z = z ₁ и учтем, что P_n ( z ₁) = 0 :
P_n ( z ₁ ) = ( z ₁ – z ₁ ) P_{n– 1} ( z ₁ ) + c ;
0 = 0 + c .
Отсюда c = 0 . Тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) ,
что и требовалось доказать.

Разложение многочлена на множители

Итак, на основании теоремы 1, многочлен P_n ( z ) имеет хотя бы один корень. Обозначим его как z ₁ , P_n ( z ₁ ) = 0 . Тогда на основании леммы 1:
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) .
Далее, если n > 1 , то многочлен P_{n– 1} ( z ) также имеет хотя бы один корень, который обозначим как z ₂ , P_{n– 1} ( z ₂ ) = 0 . Тогда
P_{n– 1} ( z ) = ( z – z ₂ ) P_{n– 2} ( z ) ;
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) P_{n– 2} ( z ) .

Продолжая этот процесс, мы приходим к выводу, что существует n чисел z ₁ , z ₂ , . , z _n таких, что
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) P ₀ ( z ) .
Но P ₀( z ) – это постоянная. Приравнивая коэффициенты при z n , находим что она равна a_n . В результате получаем формулу разложения многочлена на множители:
(1) P_n ( z ) = a_n ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) .

Числа z_i являются корнями многочлена P_n ( z ) .

В общем случае не все z_i , входящие в (1), различны. Среди них могут оказаться одинаковые значения. Тогда разложение многочлена на множители (1) можно записать в виде:
(2) P_n ( z ) = a_n ( z – z ₁ ) n ₁ ( z – z ₂ ) n ₂ . ( z – z _k ) n_k ;
.
Здесь z_i ≠ z_j при i ≠ j . Если n_i = 1 , то корень z_i называется простым. Он входит в разложение на множители в виде ( z–z_i ) . Если n_i > 1 , то корень z_i называется кратным корнем кратности n_i . Он входит в разложение на множители в виде произведения n_i простых множителей: ( z–z_i )( z–z_i ) . ( z–z_i ) = ( z–z_i ) n_i .

Многочлены с действительными коэффициентами

Далее мы считаем, что многочлен

имеет действительные коэффициенты a_i .

Лемма 2

Если – комплексный корень многочлена с действительными коэффициентами, , то комплексно сопряженное число также является корнем многочлена, .

Доказательство

Действительно, если , и коэффициенты многочлена – действительные числа, то .

Таким образом, комплексные корни входят в разложение на множителями парами со своими комплексно сопряженными значениями:
,
где , – действительные числа.
Тогда разложение (2) многочлена с действительными коэффициентами на множители можно представить в виде, в котором присутствуют только действительные постоянные:
(3) ;
.

Методы разложения многочлена на множители

С учетом сказанного выше, для разложения многочлена на множители, нужно найти все корни уравнения P_n(z) = 0 и определить их кратность. Множители с комплексными корнями нужно сгруппировать с комплексно сопряженными. Тогда разложение определяется по формуле (3).

Таким образом, метод разложения многочлена на множители заключается в следующем:
1. Находим корень z ₁ уравнения P_n ( z ₁) = 0 .
2.1. Если корень z ₁ действительный, то в разложение добавляем множитель ( z – z ₁) и делим многочлен P_n(z) на ( z – z ₁) . В результате получаем многочлен степени n – 1 :
.
Далее повторяем процесс для многочлена P_{n– 1} (z) , начиная с пункта 1, пока не найдем все корни.
2.2. Если корень комплексный, то и комплексно сопряженное число является корнем многочлена. Тогда в разложение входит множитель

,
где b ₁ = – 2 x ₁ , c ₁ = x ₁ 2 + y ₁ 2 .
В этом случае, в разложение добавляем множитель ( z 2 + b ₁ z + c ₁) и делим многочлен P_n(z) на ( z 2 + b ₁ z + c ₁) . В результате получаем многочлен степени n – 2 :
.
Далее повторяем процесс для многочлена P_{n– 2} (z) , начиная с пункта 1, пока не найдем все корни.

Нахождение корней многочлена

Главной задачей, при разложении многочлена на множители, является нахождение его корней. К сожалению, не всегда это можно сделать аналитически. Здесь мы разберем несколько случаев, когда можно найти корни многочлена аналитически.

Корни многочлена первой степени

Многочлен первой степени – это линейная функция. Она имеет один корень. Разложение имеет только один множитель, содержащий переменную z :
.

Корни многочлена второй степени

Чтобы найти корни многочлена второй степени, нужно решить квадратное уравнение:
P ₂( z ) = a ₂ z 2 + a ₁ z + a ₀ = 0 .
Если дискриминант 0″ style=»width:167px;height:22px;vertical-align:-12px;background-position:-392px -473px»> , то уравнение имеет два действительных корня:
, .
Тогда разложение на множители имеет вид:
.
Если дискриминант D = 0 , то уравнение имеет один двукратный корень:
;
.
Если дискриминант D 0 , то корни уравнения комплексные,
.

Многочлены степени выше второй

Существуют формулы для нахождения корней многочленов 3-ей и 4-ой степеней. Однако ими редко пользуются, поскольку они громоздкие. Формул для нахождения корней многочленов степени выше 4-ой нет. Несмотря на это, в некоторых случаях, удается разложить многочлен на множители.

Нахождение целых корней

Если известно, что многочлен, у которого коэффициенты – целые числа, имеет целый корень, то его можно найти, перебрав все возможные значения.

Лемма 3

Пусть многочлен
,
коэффициенты a_i которого – целые числа, имеет целый корень z ₁ . Тогда этот корень является делителем числа a ₀ .

Доказательство

Перепишем уравнение P_n ( z ₁) = 0 в виде:
.
Тогда – целое,
M z ₁ = – a ₀ .
Разделим на z ₁ :
.
Поскольку M – целое, то и – целое. Что и требовалось доказать.

Поэтому, если коэффициенты многочлена – целые числа, то можно попытаться найти целые корни. Для этого нужно найти все делители свободного члена a ₀ и, подстановкой в уравнение P_n ( z ) = 0 , проверить, являются ли они корнями этого уравнения.
Примечание. Если коэффициенты многочлена – рациональные числа, , то умножая уравнение P_n ( z ) = 0 на общий знаменатель чисел a_i , получим уравнение для многочлена с целыми коэффициентами.

Нахождение рациональных корней

Если коэффициенты многочлена – целые числа и целых корней нет, то при a_n ≠ 1 , можно попытаться найти рациональные корни. Для этого нужно сделать подстановку
z = y/a_n
и умножить уравнение на a_n n- 1 . В результате мы получим уравнение для многочлена от переменной y с целыми коэффициентами.Далее ищем целые корни этого многочлена среди делителей свободного члена. Если мы нашли такой корень y_i , то перейдя к переменной x , получаем рациональный корень
z_i = y_i /a_n .

Полезные формулы

Приведем формулы, с помощью которых можно разложить многочлен на множители.

В более общем случае, чтобы разложить многочлен
P_n ( z ) = z n – a ₀ ,
где a ₀ – комплексное, нужно найти все его корни, то есть решить уравнение:
z n = a ₀ .
Это уравнение легко решается, если выразить a ₀ через модуль r и аргумент φ :
.
Поскольку a ₀ не изменится, если к аргументу прибавить 2 π , то представим a ₀ в виде:
,
где k – целое. Тогда
;
.
Присваивая k значения k = 0, 1, 2, . n– 1 , получаем n корней многочлена. Тогда его разложение на множители имеет вид:
.

Биквадратный многочлен

Рассмотрим биквадратный многочлен:
.
Биквадратный многочлен можно разложить на множители, без нахождения корней.

Далее раскладываем квадратные многочлены на множители, если соответствующие многочлены имеют действительные корни.

Бикубический и многочлены, приводящиеся к квадратному

Рассмотрим многочлен:
.
Его корни определяются из уравнения:
.
Оно приводится к квадратному уравнению подстановкой t = z n :
a _{2 n} t 2 + a_n t + a ₀ = 0 .
Решив это уравнение, найдем его корни, t ₁ , t ₂ . После чего находим разложение в виде:
.
Далее методом, указанным выше, раскладываем на множители z n – t ₁ и z n – t ₂ . В заключении группируем множители, содержащие комплексно сопряженные корни.

Возвратные многочлены

Многочлен называется возвратным, если его коэффициенты симметричны:

Пример возвратного многочлена:
.

Если степень возвратного многочлена n – нечетна, то такой многочлен имеет корень z = –1 . Разделив такой многочлен на z + 1 , получим возвратный многочлен степени n – 1 .
Если степень возвратного многочлена n – четна, то подстановкой , он приводится к многочлену степени n/ 2 . См. Пример с возвратным многочленом >>>.

Автор: Олег Одинцов . Опубликовано: 11-06-2015 Изменено: 30-04-2016

Источник