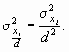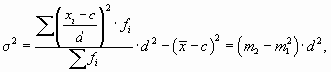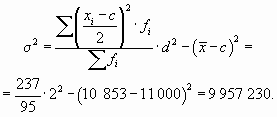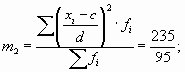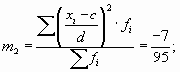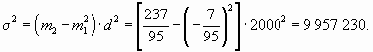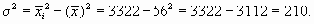Способ моментов для сгруппированного ряда

нЕФПД НПНЕОФПЧ ЪБЛМАЮБЕФУС Ч УМЕДХАЭЕН: МАВПК НПНЕОФ УМХЮБКОПК ЧЕМЙЮЙОЩ (ОБРТЙНЕТ, -К) ЪБЧЙУЙФ, ЮБУФП ЖХОЛГЙПОБМШОП, ПФ РБТБНЕФТБ . оП ФПЗДБ Й РБТБНЕФТ НПЦЕФ ПЛБЪБФШУС ЖХОЛГЙЕК ПФ ФЕПТЕФЙЮЕУЛПЗП -ЗП НПНЕОФБ. рПДУФБЧЙЧ Ч ЬФХ ЖХОЛГЙА ЧНЕУФП ОЕЙЪЧЕУФОПЗП ФЕПТЕФЙЮЕУЛПЗП -ЗП НПНЕОФБ ЕЗП ЧЩВПТПЮОЩК БОБМПЗ, РПМХЮЙН ЧНЕУФП РБТБНЕФТБ ПГЕОЛХ . рХУФШ , , ЧЩВПТЛБ ПВЯЕНБ ЙЪ РБТБНЕФТЙЮЕУЛПЗП УЕНЕКУФЧБ ТБУРТЕДЕМЕОЙК , ЗДЕ . чЩВЕТЕН ОЕЛПФПТХА ЖХОЛГЙА ФБЛ, ЮФПВЩ УХЭЕУФЧПЧБМ НПНЕОФ

Й ЖХОЛГЙС ВЩМБ ПВТБФЙНБ Ч ПВМБУФЙ . фПЗДБ Ч ЛБЮЕУФЧЕ ПГЕОЛЙ ДМС ЧПЪШНЕН ТЕЫЕОЙЕ ХТБЧОЕОЙС

йМЙ (ЮФП ФП ЦЕ УБНПЕ), УОБЮБМБ ТЕЫБЕН ХТБЧОЕОЙЕ (3) ПФОПУЙФЕМШОП , Б ЪБФЕН ЧНЕУФП ЙУФЙООПЗП НПНЕОФБ ВЕТЕН ЧЩВПТПЮОЩК :

юБЭЕ ЧУЕЗП Ч ЛБЮЕУФЧЕ ЖХОЛГЙЙ ВЕТХФ . ч ЬФПН УМХЮБЕ

Й, ЕУМЙ ЖХОЛГЙС ПВТБФЙНБ Ч ПВМБУФЙ , ФП

нПЦОП УЛБЪБФШ, ЮФП НЩ ВЕТЕН Ч ЛБЮЕУФЧЕ ПГЕОЛЙ ФБЛПЕ (УМХЮБКОПЕ) ЪОБЮЕОЙЕ РБТБНЕФТБ , РТЙ ЛПФПТПН ЙУФЙООЩК НПНЕОФ УПЧРБДБЕФ У ЧЩВПТПЮОЩН.

рХУФШ , , ЧЩВПТЛБ ПВЯЕНБ ЙЪ ТБЧОПНЕТОПЗП ОБ ПФТЕЪЛЕ ТБУРТЕДЕМЕОЙС , ЗДЕ . оБКДЕН ПГЕОЛХ НЕФПДБ НПНЕОФПЧ (пнн) РП РЕТЧПНХ НПНЕОФХ:

оБКДЕН ПГЕОЛХ НЕФПДБ НПНЕОФПЧ (пнн) РП -НХ НПНЕОФХ:

рХУФШ , , ЧЩВПТЛБ ПВЯЕНБ ЙЪ ТБУРТЕДЕМЕОЙС рХБУУПОБ У ОЕЙЪЧЕУФОЩН РБТБНЕФТПН . чЧЕДЕН ОПЧЩК РБТБНЕФТ

Й ОБКДЕН ПГЕОЛХ НЕФПДБ НПНЕОФПЧ ДМС У РПНПЭША ЖХОЛГЙЙ :

ъБНЕФЙН, ЮФП ПГЕОЛХ ДМС РБТБНЕФТБ У РПНПЭША ЖХОЛГЙЙ ОБКФЙ ОЕМШЪС: ЖХОЛГЙС ОЕ СЧМСЕФУС ЧЪБЙНОП-ПДОПЪОБЮОПК Й, УМЕДПЧБФЕМШОП, ПВТБФЙНПК РП Ч ПВМБУФЙ . пГЕОЛХ ДМС РБТБНЕФТБ ТБЪХНОП ОБИПДЙФШ РП РЕТЧПНХ НПНЕОФХ: , Й ПГЕОЛБ НЕФПДБ НПНЕОФПЧ.

нПЦЕФ УМХЮЙФШУС ФБЛ, ЮФП , ФПЗДБ ЛБЛ . ч ЬФПН УМХЮБЕ ПГЕОЛХ ЛПТТЕЛФЙТХАФ. оБРТЙНЕТ, Ч ЛБЮЕУФЧЕ пнн ВЕТХФ ВМЙЦБКЫХА Л ФПЮЛХ ЙЪ ЙМЙ ЙЪ ЪБНЩЛБОЙС .

рХУФШ , , ЧЩВПТЛБ ПВЯЕНБ ЙЪ ОПТНБМШОПЗП ТБУРТЕДЕМЕОЙС У ОЕПФТЙГБФЕМШОЩН УТЕДОЙН . йЭЕН ПГЕОЛХ ДМС РП РЕТЧПНХ НПНЕОФХ:

пДОБЛП РП ХУМПЧЙА , ФПЗДБ ЛБЛ НПЦЕФ ВЩФШ Й ПФТЙГБФЕМШОП. еУМЙ , ФП Ч ЛБЮЕУФЧЕ ПГЕОЛЙ ДМС ВПМЕЕ РПДПКДЕФ 0. еУМЙ ЦЕ , Ч ЛБЮЕУФЧЕ ПГЕОЛЙ ОХЦОП ВТБФШ . йФПЗП: «ЙУРТБЧМЕООБС» ПГЕОЛБ НЕФПДБ НПНЕОФПЧ.

Источник

Показатели вариации в статистике

7.2. Свойства дисперсии, расчет дисперсии способом моментов

Дисперсия обладает рядом математических свойств. Приведем основные из них:

если x_i = c, где с — постоянная величина, то дисперсия будет равна нулю;
если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:

На приведенных свойствах дисперсии основан один из методов ее расчета — способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):

где с — значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой);

d — величина интервалов;

— момент второго порядка;

— момент первого порядка.

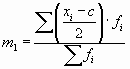
По данным табл. 7.5 определим дисперсию способом моментов.

Таблица 7.5. Расчет дисперсии способом моментов

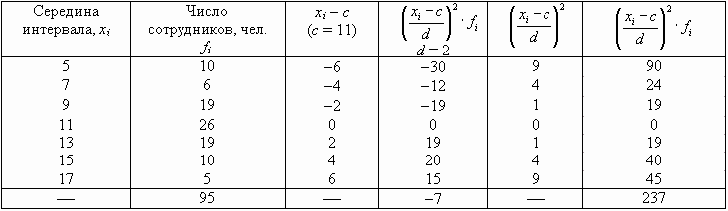Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d — единицу, то приведенная выше формула примет следующий вид:

Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней.

Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений — 3322. Определим дисперсию.

Вопросы и ответы

Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок — я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса.

Источник

Вычисление средней арифметической по способу моментов (условных отклонений)

При больших числовых значениях признака в значительных по объему сово- купностях средняя арифметическая вычисляется упрощенным способом, который называется “способ моментов” или “способ условных отклонений”.

Вычисление средней арифметической по способу моментов основано на сле- дующих ее свойствах:

Каждая варианта отклоняется от средней в большую или в меньшую сторону.

Это отклонение (d) может быть выражено положительным или отрицательным числом.

Сумма отклонений с положительным знаком всегда равна сумме отклонений с отрицательным знаком, следовательно, алгебраическая сумма отклонений всех вариант от средней равна нулю ( это свойство средней лежит в основе данного способа вычисления).

Средняя арифметическая равна любой произвольно взятой величине плюс среднее отклонение от нее всех членов ряда, которое имеет выражение Pd и называется моментом первой степени (обозначается буквой А) n

Средняя арифметическая вычисляется по формуле:

 , где М — средняя арифметическая

М₁ — “условная” средняя арифметическая

d — отклонение условной средней от вариант Р — частота

n — число наблюдений

Вычисление ведется от “условной” средней (М₁). За среднюю условно при- нимается любая варианта, чаще мода (как наиболее часто встречающаяся вариан- та). Если эта величина действительно средняя арифметическая, то сумма откло- нений всех вариант от нее будет равна нулю. Если сумма отклонений будет рав-

няться какой-то величине, то это означает, что “условная” средняя не соответст- вует действительной и к ней требуется поправка (момент первой степени — А):

ПРИМЕР: Средняя дневная нагрузка врача-терапевта в поликлинике

Число больных (V)

Число приемов (Р)

М₁ = 18; n = 22 = — 0,18

Таким образом, М = 18 + (- 0,18) = 17,82.

Последовательность вычислений: Выбираем “условную” среднюю М₁ = 18 больных

Определяем отклонение ( d ) каждой варианты от “условной” средней

Найденные отклонения умножают на частоты P  (V — M₁) = Pd Вычисляем алгебраическую сумму всех отклонений Рd = — 4 По формуле определяем среднюю арифметическую

М = М₁ + n М = 18 + 22 = 18 + (- 0,18) = 17,82

Параметры средней арифметической

Средние величины являются важными характеристиками совокупности, од- нако они полностью не раскрывают индивидуальные значения признака, которые отличаются от средних и различаются между собой. Средние величины скрывают изменчивость, колеблемость признака, его рассеянность.

При обработке вариационного ряда недостаточно только лишь вычислить среднюю арифметическую, нужно еще оценить, насколько она типична и досто- верна для данной совокупности. Для этого в статистике существуют специальные параметры средней — мера типичности и мера достоверности.

ОЦЕНКА ТИПИЧНОСТИ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ

Чем вариационный ряд более компактен, менее рассеян, тем лучше средняя арифметическая характеризует данную совокупность.

Если вариационный ряд растянут, отдельные значения вариант сильно от- клоняются от средней (т.е. имеется большая вариабельность, колеблемость при- знака), то средняя хуже характеризует ряд в целом и является менее типичной для данной совокупности.

Таким образом, кроме средней необходима еще одна характеристика ряда: его колеблемость.

Простейшей мерой колеблемости ряда является амплитуда (вариационный размах), т.е. разность крайних вариант. Например, при подсчете частоты пульса у одной группы обследованных средняя составляла 68, минимальное число было 60, а максимальное — 70. У второй группы средняя частота пульса составляла так- же 68, но наименьшее число было 55, а наибольшее — 80. Амплитуда в первой группе значительно меньше и, следовательно, все значения группируются вокруг средней. Вторая совокупность более разнообразна, ее рассеяность велика и коле- бания отдельных значений от средней больше; следовательно, средняя в этой группе менее типична , чем в первой группе.

Мерой колеблемости, изменчивости признака и мерой типичности средней арифметической является среднее квадратическое отклонение (сиг- ма — ), которое определяется по формуле (по способу моментов):

ПРИМЕР: Результаты измерения массы тела мальчиков 12 лет

Источник

Способ моментов для сгруппированного ряда

(Параметрические моменты от кинетических кривых в обработке и интерпретации результатов диффузионных экспериментов)

— 1987 и 2007 —

Содержание

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1.1 Распределения случайные величины
1.2 Характеристики распределений
1.2.1 Математическое ожидание (среднее арифметическое)
1.2.2 Медиана и мода
1.2.3 Квартили и квантили
1.2.4 Дисперсия
1.2.5 Моменты
1.2.6 Гистограмма
1.2.7 Моменты многомерной случайной величины
1.3 Функции от случайных величин
1.4 Характеристические функции
МОМЕНТЫ И КАРТА ПИРСОНА
2.1 Эмпирические моменты
2.2 Карта Пирсона
2.2.1 Семейство кривых Пирсона
2.2.2 Стандартные статистические распределения на карте Пирсона
МОМЕНТЫ В ДИФФУЗИИ
3.1 Моменты от кривых, заданных аналитически
3.1.1 Проницаемость
3.1.1.1 Классическая диффузия
3.1.1.2 Параллельная диффузия по нескольким независимым каналам
3.1.1.3. Проницаемость + необратимая химическая реакция 1-го порядка (радиоактивный распад).
3.1.1.4 Проницаемость набухающей мембраны
3.1.1.5 Проницаемость + обратимая химическая реакция 1-го порядка (диффузия в дефектных средах)
3.1.1.6 Диффузия по двум каналам с обратимым обменом между ними
3.1.2 Электрохимический вариант метода проницаемости
3.1.3 Кинетика диффузии одного скачка
3.1.4 Сорбционно-десорбционный метод
3.1.4.1 Сорбция пластиной
3.1.4.2 Сорбция сферой
3.1.4.3 Сорбция цилиндром, h=R
3.1.4.4 Сорбция полубесконечной средой
3.2 Моменты от функций, заданных в изображении
3.2.1 Применение ряда Лорана и теории вычетов
3.2.1.1 Классическая проницаемость
3.2.1.2 Проницаемость при граничных условиях 3-го рода на обеих поверхностях мембраны
3.2.1.3 Проницаемость пластины при граничных условиях I – III
3.2.2 Метод моментов в операционном исчислении
3.2.2.1 Распределение концентрации при проницаемости
3.2.2.2 Локальные потоки в мембране при классической проницаемости
3.2.2.4 Локальные моменты при сорбции пластиной
3.2.2.4 Локальные моменты при сорбции сферой
3.2.2.5 Локальные моменты при сорбции цилиндром
3.2.2.5 Проницаемость пластины при переменных граничных условиях
3.3 Сорбция дисперсионными средами
3.3.1 Сорбция сферическим образцом, содержащим дисперсию сферических включений второй фазы
3.3.2 Сорбция газа образцом произвольной формы, содержащим включения произвольной формы
3.3.2.1 Общий случай
3.3.2.2 Сорбция пластиной со сферическими включениями
3.3.2.3 Сорбция пластиной, начинённой шайбами
3.3.2.4 Сорбция пластиной с цилиндрическими включениями
3.2.2.5 Сорбция сферой с цилиндрическими включениями
3.3.2.6 Сорбция полой цилиндрической оболочкой со сферическими включениями
3.3.2.7 Сорбция при наличии граничных условий 3-го рода на поверхности включений
3.3.2.8 Сорбция и замкнутого объёма (резервуара небольшой ёмкости)
3.3.2.9 Сорбция сферой, содержащей сферические включения различных размеров
3.3.2.10 Сорбция цилиндрическим образцом с непроницаемыми торцами, содержащим включения сферической формы
3.4 Моменты от функций, заданных дифференциальным уравнением в частных производных
3.4.1 Проницаемость при наличии концентрационной зависимости коэффициента диффузии
3.4.2 Проницаемость слоистых сред (последовательная диффузия)
3.4.3 Проницаемость среды с точечными дефектами ограниченной ёмкости
ПРИМЕНЕНИЕ МЕТОДА МОМЕНТОВ ДЛЯ РЕШЕНИЯ НЕКОТОРЫХ ДИФФУЗИОННЫХ ЗАДАЧ
4.1 Поправки на инерционность аппаратуры
4.2 Сведение диффузионных уравнений к известным статистическим распределениям
4.3 Определение параметров диффузии
4.3.1 Сорбция дисперсионными средами
4.3.2 Метод термодесорбционной спектроскопии
4.3.4 Диагностика диффузионных процессов
4.3.5 Использование метода моментов в планировании диффузионного эксперимента
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
5.1 Компьютерный эксперимент
5.2 Финитные распределения
5.2.1 Обрезка «хвоста»
5.2.2. Обрезка снизу
5.2.3 Диагностика моделей при наличии шумов
ДИФФУЗИОННАЯ КАРТА БЕКМАНА
6.1 Показатели асимметрии и эксцесса в диффузии
6.2 Статистические распределения на карте Бекмана
6.2 Диффузионные ситуации на карте Бекмана
6.2.1 Классическая диффузия
6.2.2 Параллельная диффузия по двум независимым каналам
6.2.3 Про ницаемость + необратимая химическая реакция 1-го порядка
6.2.4 Проницаемость + обратимая химическая реакция 1-го порядка
6.2.5 Сорбция дисперсионными средами
6.2.6 Сорбция дефектными средами
6.2.7 Анализ формы кривых термостимулированного газовыделения методом моментов
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ МЕТОДА МОМЕНТОВ
Литература
ПРИЛОЖЕНИЕ

АННОТАЦИЯ

Метод моментов – важная часть компьютерного комплекса DIGS, предназначенного для обработки результатов экспериментов по изучению диффузии газов в твёрдых телах. Предлагаемый обзор демонстрирует способы использования параметрических моментов, рассчитанных по кинетическим кривым диффузии, для оценки параметров математических моделей, содержащих несколько (два – три) неизвестных параметра. Серьёзное внимание уделено перспективам применения метода статистических моментов и карты Пирсона для анализа сложных диффузионных ситуаций, не требующих использования какой-либо априорной информации об исследуемом процессе. В качестве вспомогательного материала приведены сведения из стандартного курса по математической статистике, касающиеся известных функций и распределения плотностей вероятности, выборок, гистограмм, моментам различных уровней, квантилям, квартилям и т.п. Даны примеры применения метода момента для оценки параметров диффузии газов (как стабильных, так и радиоактивных), измеренных методом проницаемости, сорбции-десорбции и термодесорбционой спектроскопии в активных (адсобционно – или химически) гетерогенных средах переменного состава и структуры.

ПРЕДИСЛОВИЕ

Данный обзор обобщает наши усилия, направленные на оценку перспектив использования статистических моментов от кинетических диффузионных кривых для анализа сложных диффузионных ситуаций. Основное внимание здесь уделено попыткам создания методик, не требующих какой-либо априорной информации о механизме изучаемого процесса. Действительно, мы не должны навязывать природе свой закон, перебирая все мыслимые и немыслимые варианты, и выбирая тот, который оказался ближе к эксперименту. Наоборот, закон сам собой должен выходить из экспериментальных данных. Не менее важным представляется возможность использования довольно просто и достаточно точно (с использованием всех точек кривой) рассчитываемых из экспериментальной кинетической кривой первых начальных моментов для оценки нескольких параметров моделей, математический аппарат которых не допускает решения исходных диффузионных уравнений (например, диффузия + обратимая химическая реакция 2-го порядка) или решение не может быть выражено аналитическими функциями (например, последовательная диффузия в слоистой среде).

Первая часть работы содержит некоторые, вообще говоря, хорошо известные сведения из области математической статистики, необходимые для понимания дальнейшего текста. Вводятся понятия начальных, центральных и основных моментов, приводятся примеры статистических распределений и соответствующих им моментов. Во второй части мы переходим к карте Пирсона и обсуждаем её возможности в плане описания каких-то реальных физических экспериментов статистическими распределениями и в плане исследования явлений без использования какой-либо априорной информации. Остальная часть обзора посвящена диффузии, причём, как типично для нашей лаборатории – диффузии газов в твёрдых телах, измеряемой методами проницаемости, сорбции-десорбции, термодесорбционной спектроскопии и др. Здесь даны способы нахождения моментов по готовым аналитическим решениям диффузионных уравнениям, по решениям, существующим только в изображениях, а также по самим исходным дифференциальным уравнениям, без их решения. Рассмотрены такие диффузионные ситуации, как классическая (ненарушенная) диффузия в средах с различной простой геометрией и разными краевыми условиями, диффузия при наличии необратимой или обратимой химической реакции 1-го порядка, диффузия в слоистых средах (параллельная и последовательная), диффузия в дисперсионных (наполненных или микропористых) средах, диффузия при коэффициенте диффузии, зависящем от времени или концентрации диффузанта и др. На первом этапе для анализа диффузионных ситуаций используется карта Пирсона-Бекмана, т.е. статистическая карта Пирсона на базе основных моментов, приспособленная для решения диффузионных задач, на втором этапе – диффузионная карта Бекмана, построенная на показателях асимметрии и эксцесса, и имеющая ряд мелких отличий от карты Пирсона.

Попутно решается более простая задача – определение параметров двух и трёх-параметрических моделей (т.е. осуществляется переход к более сложному классу задач по сравнению с решаемыми методами функциональных масштабов). Показано, что для анализа многих практически важных ситуаций двух начальных параметрических момента (определяемых довольно точно) вполне достаточно.

В обзоре приведены обширные данные по математическому моделированию и приведены некоторые примеры программ в системе MATHCAD.

ВВЕДЕНИЕ

Для осуществления обработки результатов физико-химических экспериментов нелинейным вариантом метода наименьших квадратов нужно располагать хорошими начальными оценками параметров. В случае двух параметров такая оценка может быть получена методом линеаризации с использованием специального функционального масштаба. При большом числе параметров модели такой подход невозможен. Выходом из положения является использование метода, основанного на расчёте параметрических моментов (математического ожидания, дисперсии, асимметрии и др.) от выборки, кинетической кривой, спектра и т.п. Преимущество такого подхода заключается в использовании для оценки параметров всех точек кривой. Попутно появляется возможность выделить собственно физический процесс на фоне сопровождающих его побочных процессов (например, отделить кинетику проницаемости газа через мембрану от процессов диффузии в подводящих трубках, сорбции на стенках и т.п.).

Второй проблемой является свёртка информации с тем, чтобы получить возможность сравнения формы различных кривых, т.е. необходимость представления информации о распределении случайной величины через несколько описывающих его параметров. В этом случае метод моментов оказывается чрезвычайно полезным, так как позволяет описать основные особенности формы кинетической кривой четырьмя начальными моментами, тремя центральными и двумя основными моментами. (Например, любое распределение гауссовского типа характеризуется точкой с координатами (0, 0) на карте Пирсона, построенной на показателях асимметрии и эксцесса).

Часто приходится сталкиваться со случаем, когда неизвестна форма рассматриваемого распределения, однако всё же представляет интерес вычисление главных показателей на основе имеющихся данных. Исторически первым общим методом оценивания параметров был метод моментов, предложенный К.Пирсоном. Идея метода заключается в том, что рассчитываются моменты от экспериментально измеренной выборке случайной величины, из них составляется система уравнений, решение которой даёт оценки параметров искомой модели.

Метод моментов позволяет аппроксимировать неизвестную физическую закономерность каким-либо хорошо известным статистическим распределением (например, одним из типов распределения Пирсона или Джонсона) и тем самым поставить обработку результатов эксперимента на прочную статистическую основу. Особенно это важно при записи доверительных интервалов для оценки параметров.

Наконец, метод моментов позволяет рассчитывать на создание алгоритма дискриминации моделей, не требующего априорной информации о физическом процессе.

Исторически метод моментов зародился в сфере статистической обработки выборок, где он применялся для проверки гипотез о типе статистического распределения случайной величины. В последние годы он начинает переноситься на обработку непрерывных функциональных зависимостей, ибо любую ограниченную нормированную функцию y=f(x) (y ≥ 0, 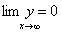на всей области определения функции) можно рассматривать как плотность распределения случайной величины х и, следовательно, применять к ней все понятия математической статистики.

Источник