- Вычисление средней арифметической по способу моментов
- Решения задач методом моментов
- Примеры решений
- Теория по методу моментов
- Расчет средней арифметической величины способом моментов
- Определение средней арифметической по способу моментов. Свойства средней арифметической
- Алгоритм нахождения средней по способу моментов
- Алгоритм нахождения средней по способу моментов
Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;
S — знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р — частота встречаемости вариант; n — число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
| V(n в кг) | Р | а (V-А) | а . Р |
| +2 | +4 | ||
| +1 | +3 | ||
| Мо=62 | |||
| -1 | -6 | ||
| -2 | -8 | ||
| -3 | -3 | ||
| п = 25 | Sар = — 10кг |
Этапы расчета средней по способу моментов:
1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;
2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).
3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;
4) находим сумму Sа . р = — 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i SаР = 62 — 1×0,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
| Ряд 1 | Ряд 2 | |
| Окружность головы(в см) Частота | 41, 45, 46, 47, 48 7, 8, 25, 6, 2 | 42, 43, 44, 45, 46, 47, 48, 49, 50 1, 2, 4, 6, 14, 10, 3, 0, 2 |
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение (s)
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
Источник
Решения задач методом моментов
Для оценивания неизвестных параметров статистических распределений наравне с методом наибольшего правдоподобия используют метод моментов.
Суть метода: выразить числовые параметры теоретического распределения через моменты распределения, оценненные по выборки. Число моментов должно соответствовать числу неизвестных параметров распределения (чаще всего используют первые два момента). После вычисления приравниваем теоретические и выборочные моменты друг к другу и выражаем оценки параметров.
Данный метод прост в в реализации, дает неплохие оценки и удобен для отработки навыков. Про свойства оценок: состоятельность оценок выполняется при непрерывной зависимости от параметра, асимптотическая эффективность оценок, полученных по ММП всегда лучше чем у ММ, оценки по ММ чаще всего смещенные (требуется проверка).
Примеры нахождения оценок по методу моментов для разных распределений вы найдете ниже. Удачи!
Примеры решений
Пример 1. Число семян сорняков в пробах зерна подчинено закону Пуассона. Имеется выборка проб зерна. Результаты записаны в таблице Т1. Найти параметр $\lambda$ по выборке методом моментов.
Пример 2. При условии равномерного распределения случайной величины $Х$ произведена выборка
3 5 7 9 11 13 15 17 19 21
21 16 15 26 22 14 21 22 18 25
Найти оценку параметров $a$ и $b$ по методу моментов.
Пример 3. Найти методом моментов по выборке $x_1, x_2, . x_n$ точечную оценку параметра $p$ биномиального распределения $P_m(x_i)=C_
Пример 4. Найти методом моментов по выборке $x_1, x_2, . x_n$ точечные оценки неизвестных параметров $a$ и $\sigma$ нормального распределения.
Пример 5. Пусть случайная величина $\xi$ имеет плотность $p(x)=1/(b-a)$, если $x\in(a;b)$, и $p(x)=0$, иначе. Произведена выборка. Используя метод моментов, найти $a$ и $b$.
Теория по методу моментов
Хотите немного больше знать о теоретических основах метода моментов для чайников? Материалов в интернете к сожалению не так много, подойдут классические учебники по математической статистике и конечно же лекция Черновой Н. по методу моментов с теоретическими основами и примерами решений.
Источник
Расчет средней арифметической величины способом моментов



Этот способ расчета средней арифметической величины основан на использовании ее математических свойств. Среднюю арифметическую величину вычисляют по формуле
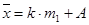
где 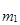
k – величина равного интервала или любое постоянное число, отличное от нуля;
А – любое постоянное число.
Момент 1-го порядка вычисляют по формуле
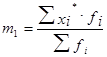
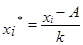
Пример 3. По исходным данным примера 2 вычислить средний размер премии одного работника способом моментов.
Решение. Пусть А = 6 000 и k = 500. Расчеты представлены в таблице:
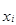 | 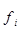 | 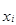 | 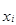 – 6000 – 6000 | 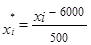 | 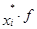 |
| 3 000–5 000 | 4 000 | – 2 000 | – 4 | – 16 | |
| 5 000– 7000 | 6 000 | ||||
| 7 000–10 000 | 8 500 | 2 500 | |||
| 10 000–15 000 | 12 500 | 6 500 | |||
| Итого |
Вычислим момент первого порядка
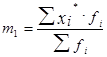
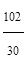
Средний размер заработной платы одного работника составил
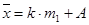
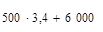
Источник
Определение средней арифметической по способу моментов. Свойства средней арифметической
Где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала,
Назначение сервиса . С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word .
Инструкция . Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Алгоритм нахождения средней по способу моментов
Пример . Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану.
Таблица для расчета показателей.
| Группы | Середина интервала, x i | Кол-во, f i | x i ·f i | Накопленная частота, S | (x-x ) 2 ·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x 0 – начало модального интервала; h – величина интервала; f 2 –частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов . 
| x ц | x * i | x * i f i | 2 f i |
| 7.5 | -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
| 27.5 | 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |

Среднее квадратическое отклонение .
мин.
Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v . С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word .
Инструкция . Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Алгоритм нахождения средней по способу моментов
Пример . Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану.
Таблица для расчета показателей.
| Группы | Середина интервала, x i | Кол-во, f i | x i ·f i | Накопленная частота, S | (x-x ) 2 ·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x 0 – начало модального интервала; h – величина интервала; f 2 –частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
.
Источник












