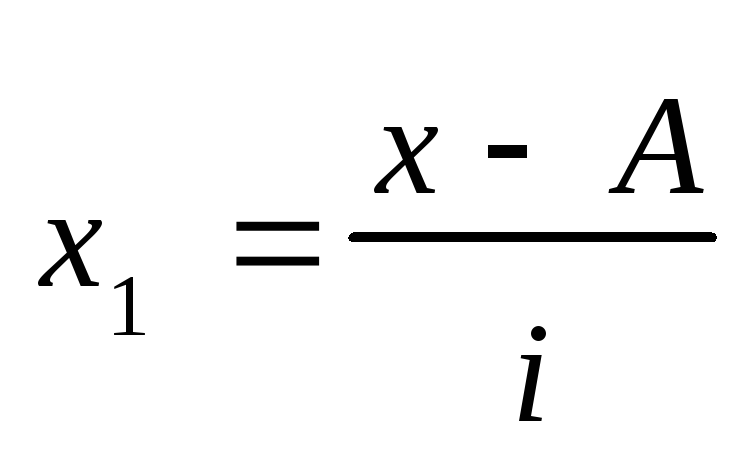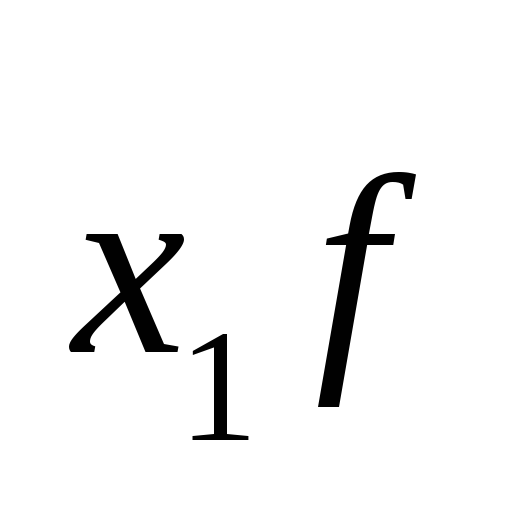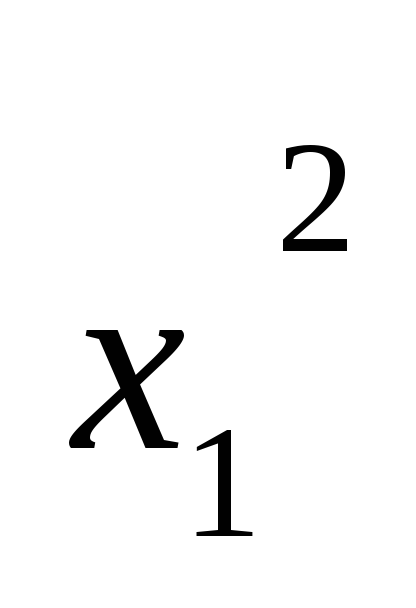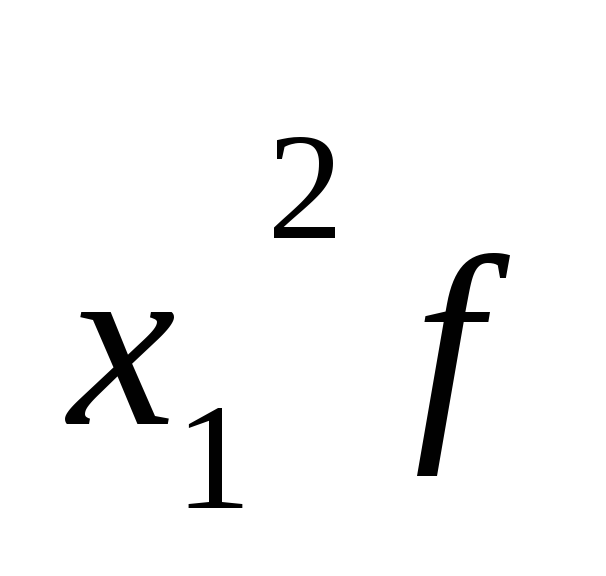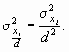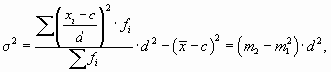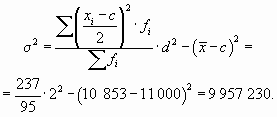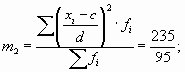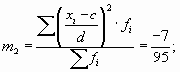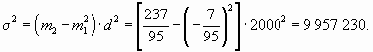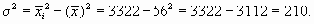Метод моментов
Содержание:
- Примеры с решением
| Метод моментов |
Метод моментов, предложенный английским статистиком Карлом Пирсоном в 1894 г., заключается в приравнивании определенного числа выборочных моментов к соответствующим теоретическим, которые являются функциями неизвестных параметров 
Рассматривая количество моментов, равное числу к неизвестных параметров, подлежащих определению, и решая полученные уравнения относительно этих параметров, получаем искомые оценки. Иначе говоря, оценки параметров 
являются решениями систем уравнений 
или 
, для некоторых 
Метод моментов содержит неопределенность, поскольку можно получить уравнения для неизвестных параметров 
, используя как начальные, так и центральные моменты, а также некоторые их модификации типа асимметрии или эксцесса.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Пример:
Функция
задает плотность распределения Рэлея (см. § 6.4). Требуется оценить параметр 
по выборке 
Найдем оценку параметра 0, приравнивая начальные выборочные и теоретические моменты. Первый начальный момент
имеет вид: 
Приравнивая, получаем первую оценку параметра: 
Приравнивая вторые начальные моменты, можем получить другую оценку: 
из уравнения, которое получитсяся при использовании второго центрального момента (дисперсии), — третью оценку: 
- Часто полагают, что для нахождения оценки одного параметра следует брать первый момент, для двух — первые два момента и т.п. По возможности действительно имеет смысл поступать так, поскольку это проще всего. Однако такой подход годится не всегда. Он не проходит, например, если некоторые моменты равны нулю или не зависят от нужных параметров.
В общем случае система уравнений для моментов может не иметь решения в элементарных функциях (и тогда можно искать решение приближенными методами) или вообще оказаться неразрешимой (несовместной).
Оценки, полученные методом моментов, часто оказываются смешенными. К достоинствам метода моментов следует отнести его простую вычислительную реализацию, а также то, что оценки являются функциями от выборочных моментов.
В силу теоремы Слуцкого любая непрерывная функция от выборочных моментов функции сходится по вероятности к постоянной, получаемой подстановкой в эту функцию теоретических моментов, если они существуют и если получаемая таким образом постоянная конечна. Для определенности рассмотрим функцию 
от двух моментов (начальных или центральных), хотя ее можно обобщить на любое конечное число аргументов, в том числе и на случай, когда Н зависит только от одного аргумента.
Теорема 1. (Крамера). Пусть в некоторой окрестности точки 
функция 
непрерывна и имеет непрерывные частные производные первого и второго порядка:
Тогда для любой выборки, по которой найдены оценки 
, случайная величина 
асимптотически нормальна при 
следующими параметрами:
Иногда оценки, получаемые с помощью метода моментов, принимаются в качестве первого приближения, по которому можно построить другими методами оценки более высокого качества.
Оценки метода моментов используются также, когда существует необходимость оценить не сами параметры распределения (которые часто представляют собой некие абстракции), а определенные практически значимые показатели, зависящие от этих параметров функционально: 
. Самый простой (хотя и не самый точный) способ такого оценивания — подставить полученные оценки в соответствующую функцию: 
Если распределение определяется одним параметром, то для построения оценки один теоретический момент приравнивают к одному эмпирическому моменту того же порядка (обычно первого).
Возможно вам будут полезны данные страницы:
Источник
6.2. Вычисление дисперсии и среднего квадратического отклонения «способом моментов»
«Способ моментов» основан на математических свойствах дисперсии. Для рядов распределения с равными интервалами расчет дисперсии можно произвести по следующей формуле:
,
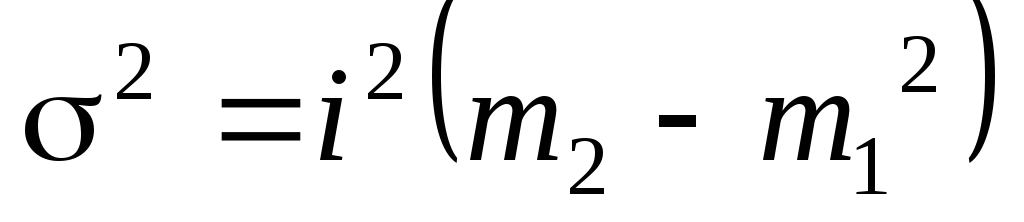
где i – размер интервала;
m1 – момент первого порядка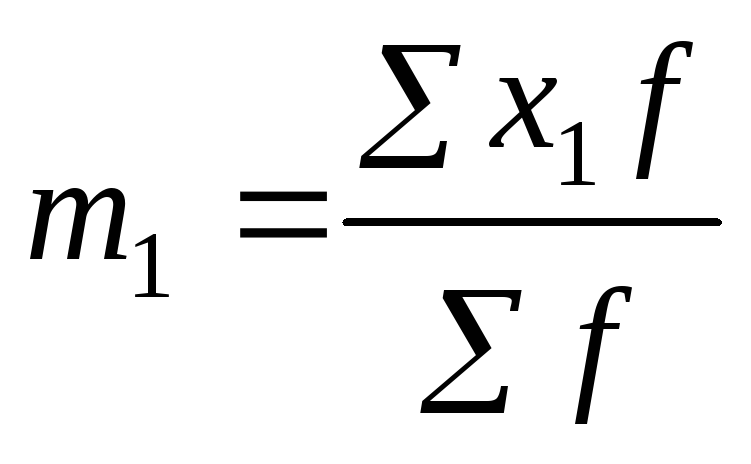 
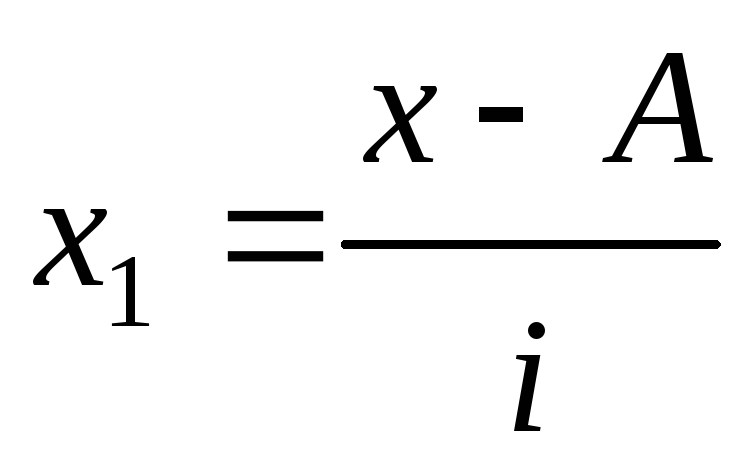
(х1 – упрощенные варианты; 
);
m2 – момент второго порядка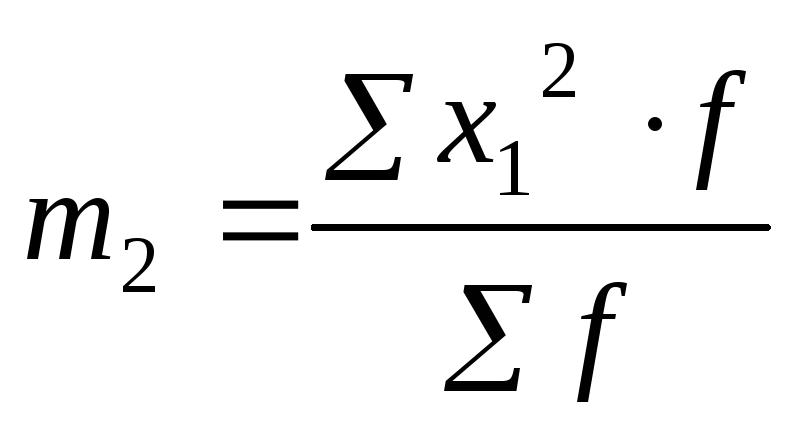 
.
Рассмотрим применение «способа моментов» в расчете дисперсии и среднеквадратического отклонения на примере следующих данных.
Пример 2. Расчет дисперсии и среднего квадратического отклонения необходимо провести по данным условия предыдущей задачи. Расчеты следует оформить в табл. 20.
Группировка работающих по возрасту, лет (х)
Удельный вес работающих, % ( f )
Середина интервала (х)
Размер интервала i = 10, А = 35 (варианта с наибольшей частотой):
;
;
;
лет.
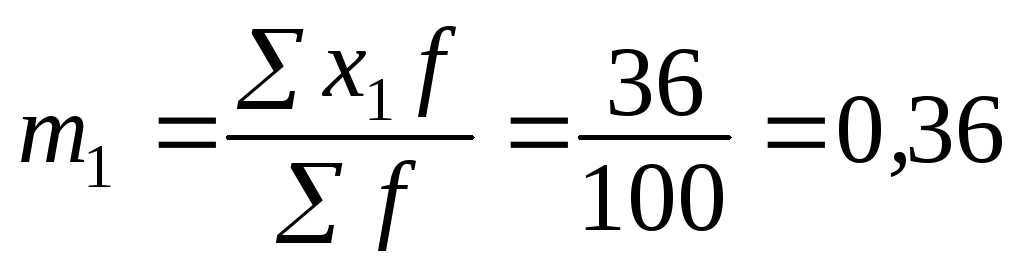
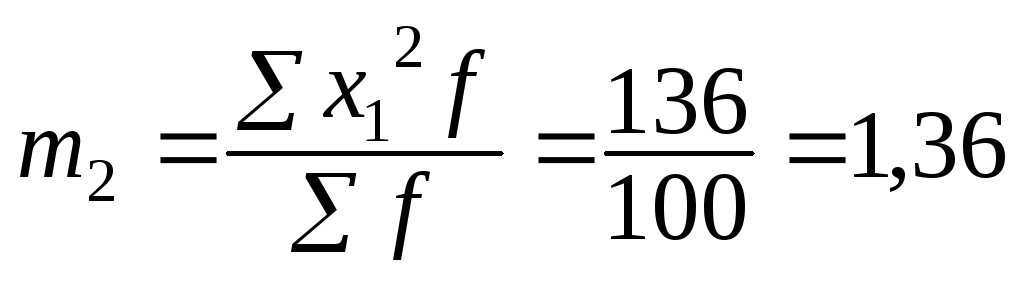
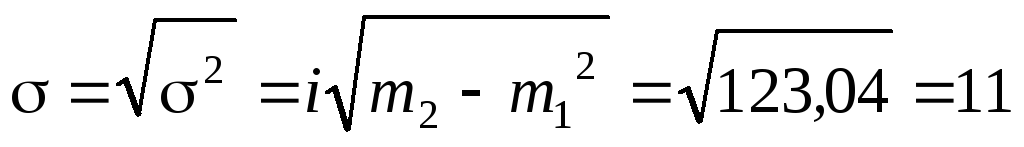
Признаки, которыми обладают одни единицы совокупности и не обладают другие, называются альтернативными. Вариацию качественных признаков можно определить, рассчитав дисперсию альтернативного признака (дисперсию доли) по формуле
,
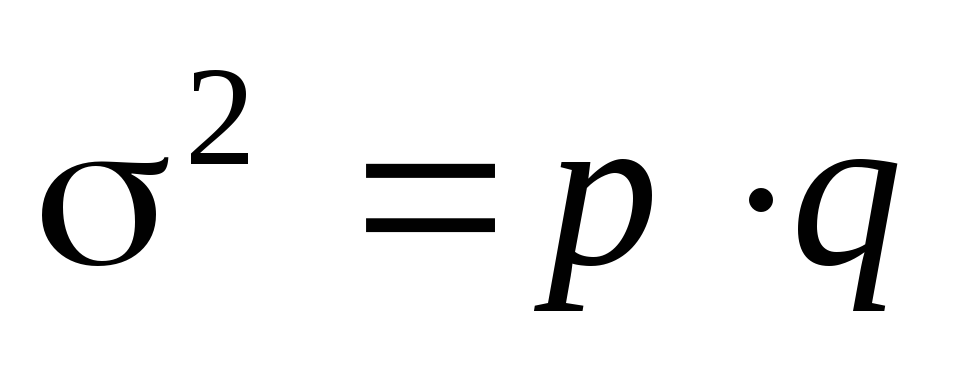
где р – доля единиц, обладающих изучаемым признаком;
q– доля единиц, не обладающих этим признаком.
В связи с тем, что p + q = 1, то q = 1 – p, следовательно,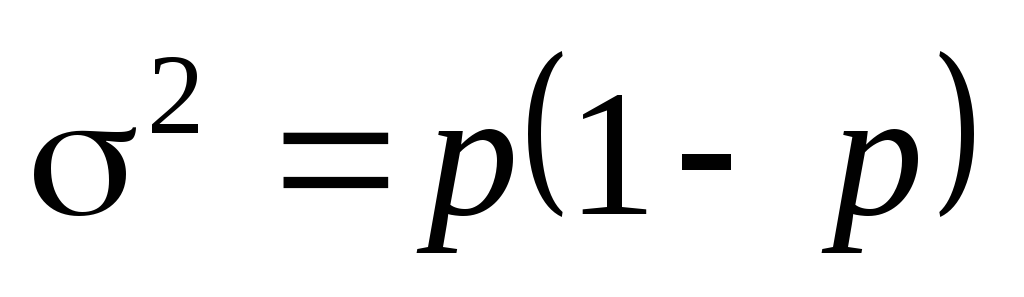 
.
Определим вариацию качественного признака в следующем примере.
Пример 3. Имеются следующие данные по Республике Беларусь (на конец 1998 г.): всего заняты в народном хозяйстве – 4416,6 тыс. чел., из них имеют высшее образование – 870,1 тыс. чел.
Необходимо определить дисперсию и среднее квадратическое отклонение доли занятых в народном хозяйстве и имеющих высшее образование.
Рассчитаем дисперсию альтернативного признака по формуле
,
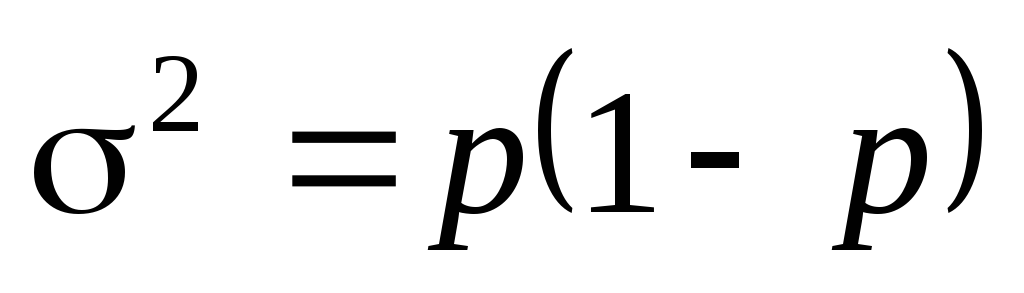
где р – доля единиц, обладающих интересующим нас признаком.
Произведем следующие расчеты:
;
;
.
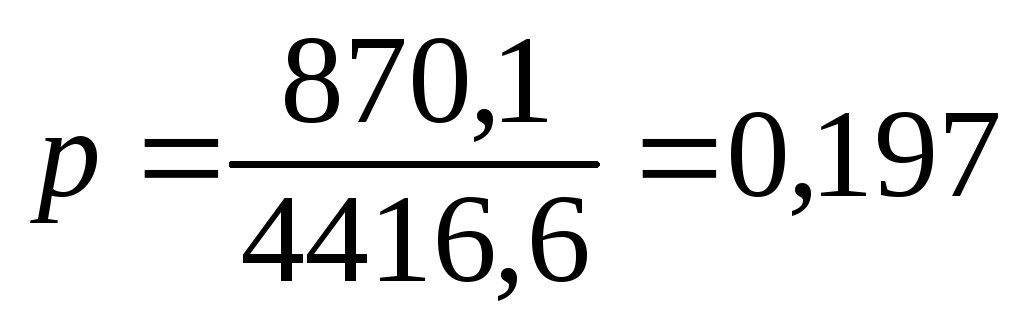
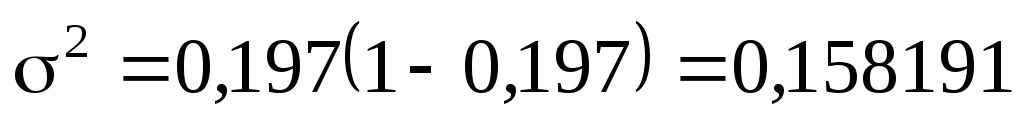
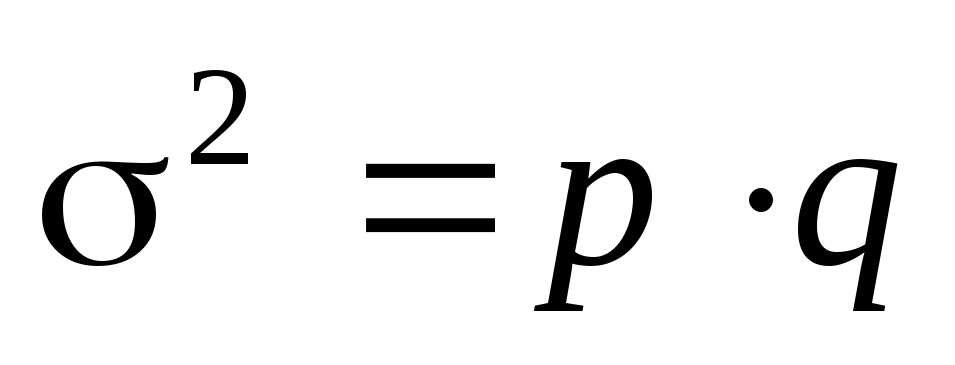
Исчислим среднее квадратическое отклонение следующим образом:
.
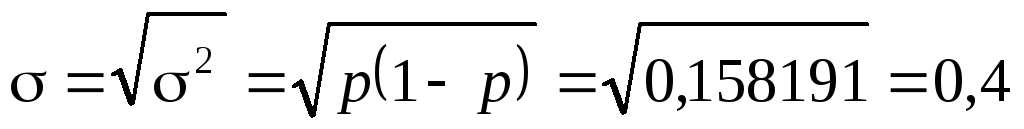
6.3. Внутригрупповая и межгрупповая вариации
Вариация признака определяется различными факторами.
Вариация, обусловленная влиянием фактора, положенного в основу группировки, называется межгрупповой вариацией и характеризуется межгрупповой дисперсией ( 2 ).
Межгрупповая дисперсия является мерой колеблемости частных (групповых) средних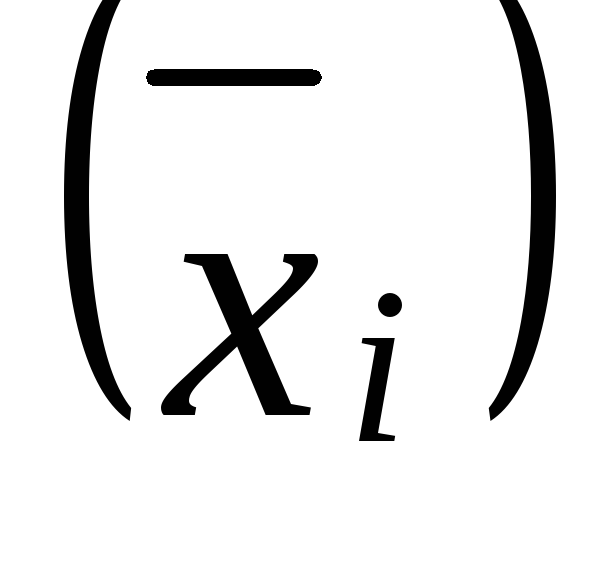 
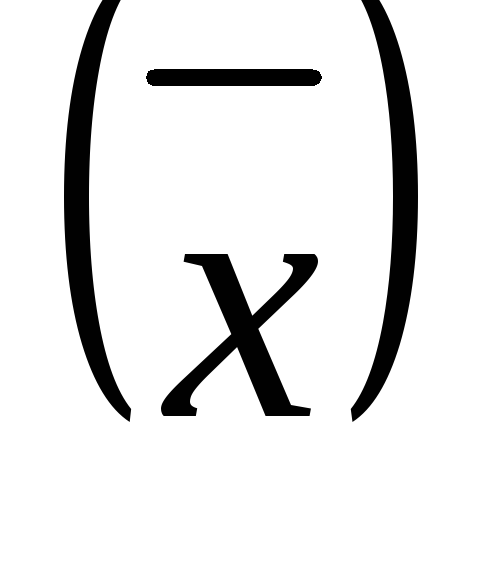
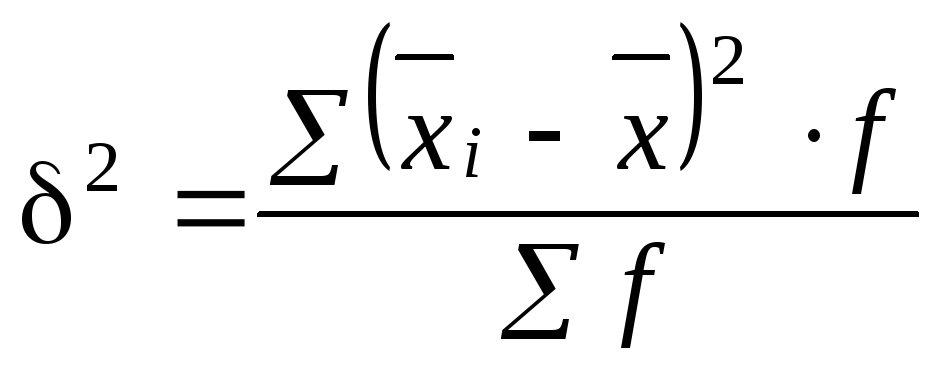
около общей средней 
и исчисляется по формуле
,
где f – количество единиц совокупности в каждой i-й группе.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия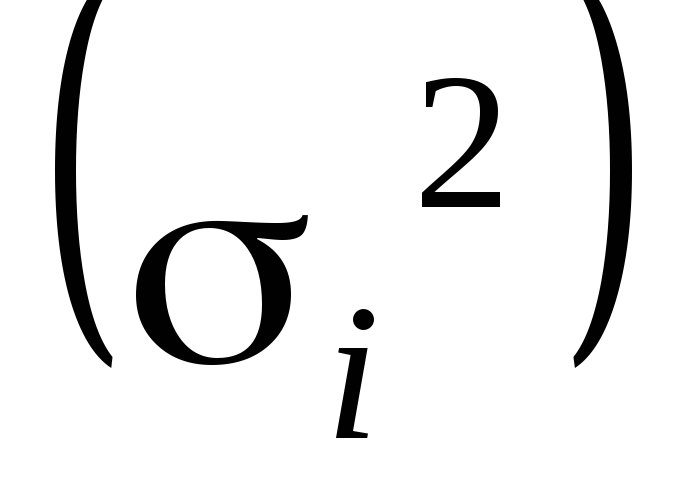 
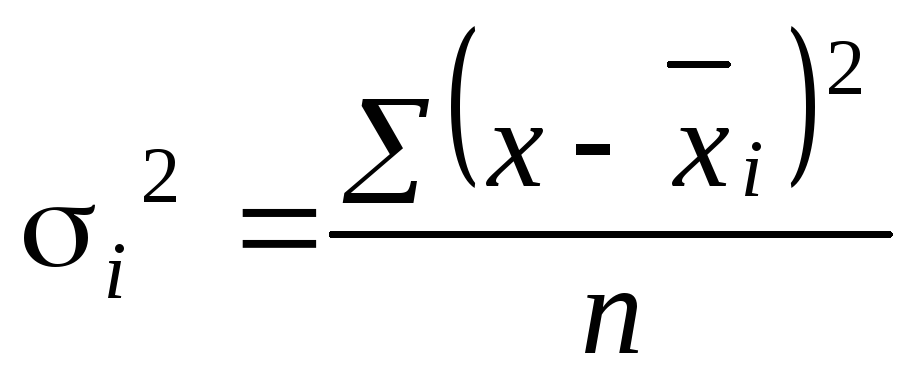
, которую определяют по следующей формуле:
.
Средняя из внутригрупповых, или частных дисперсий определяется по формуле средней арифметической взвешенной дисперсий групп
.
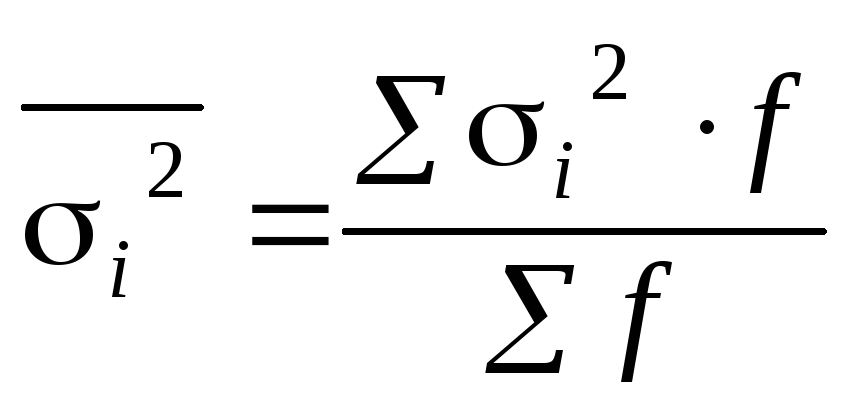
Общая дисперсия признака равна сумме межгрупповой и средней арифметической внутригрупповых дисперсий:
.
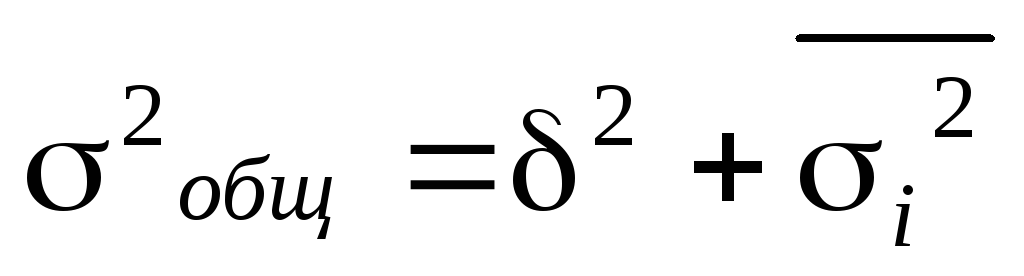
Отношение межгрупповой дисперсии к общей дает коэффициент детерминации ( 2 ). Данный коэффициент характеризует, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки:
.
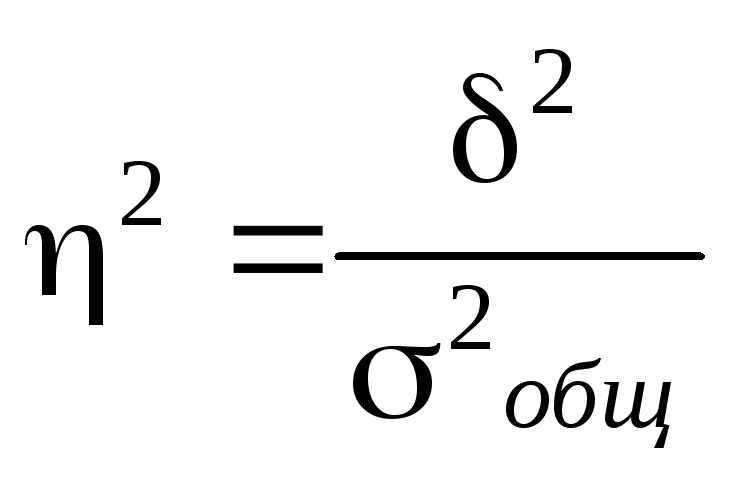
Корень квадратный из коэффициента детерминации дает эмпирическое корреляционное отношение, которое характеризует тесноту связи между группировочным и результативным признаками:
.
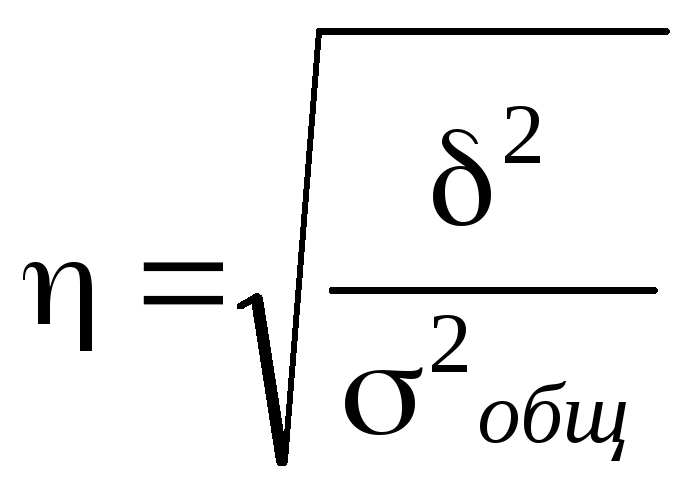
Этот показатель изменяется от 0 до 1.
Определим перечисленные выше показатели.
Пример 4. Расчеты σ 2 общ необходимо провести по данным примера 1, рассматриваемого в теме 3 (см. сводную групповую табл. 3).
Расчет межгрупповой дисперсии следует произвести по формуле
.
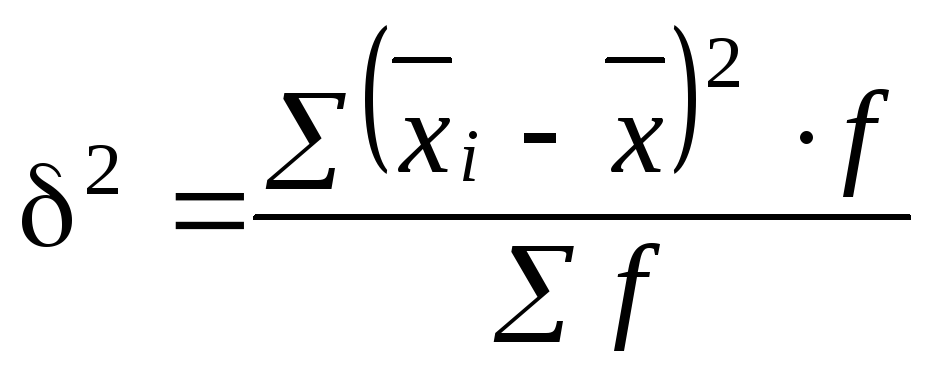
Вспомогательные расчеты необходимо оформить в табл. 21.
Источник
Показатели вариации в статистике
7.2. Свойства дисперсии, расчет дисперсии способом моментов
Дисперсия обладает рядом математических свойств. Приведем основные из них:
- если xi = c, где с — постоянная величина, то дисперсия будет равна нулю;
- если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:
На приведенных свойствах дисперсии основан один из методов ее расчета — способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):
где с — значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой);
d — величина интервалов;
— момент второго порядка;
— момент первого порядка.
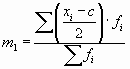
По данным табл. 7.5 определим дисперсию способом моментов.
 |
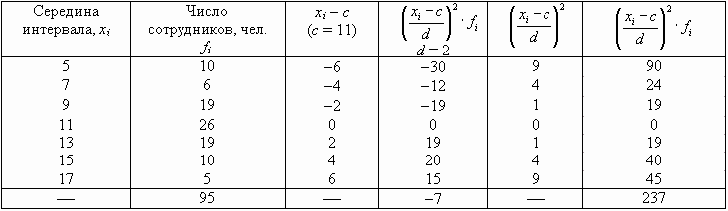Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d — единицу, то приведенная выше формула примет следующий вид:
Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней.
Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений — 3322. Определим дисперсию.
Вопросы и ответы
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок — я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса.
Источник
