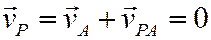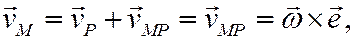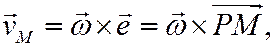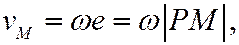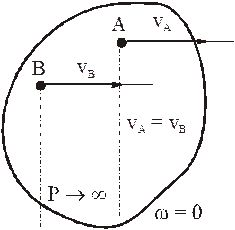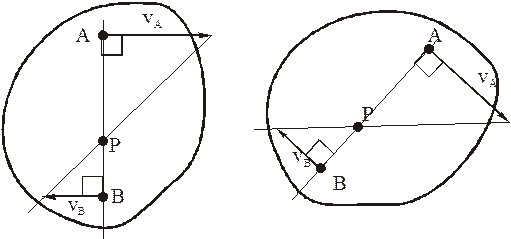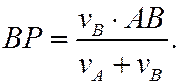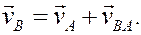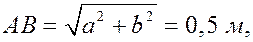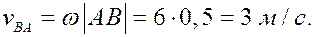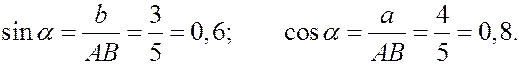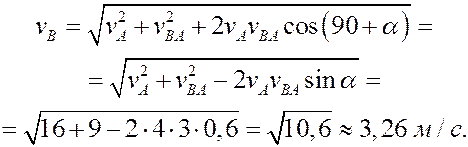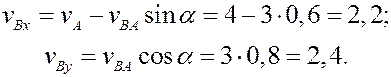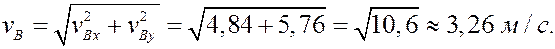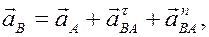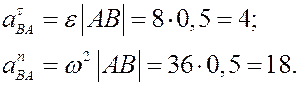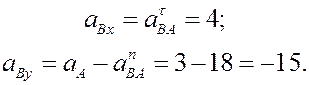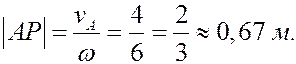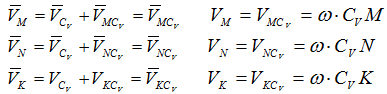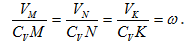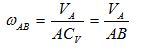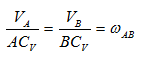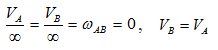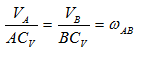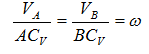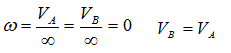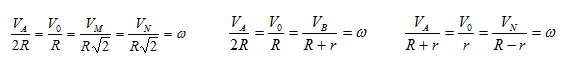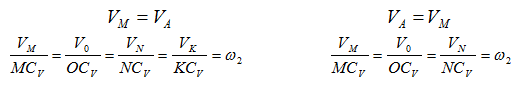Мгновенный центр скоростей (МЦС) и его определение. Определение скоростей точек тела с помощью МЦС
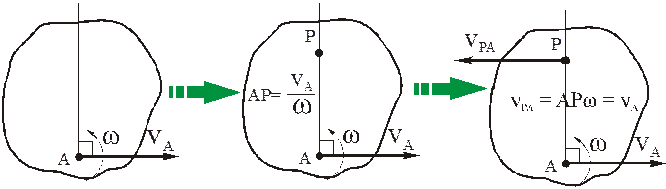
Мгновенным центром скоростей (МЦС) называется такая точка плоской фигуры, скорость которой в данный момент времени равна нулю.
При любом непоступательном движении плоской фигуры такая точка всегда существует. Действительно,
Пусть в данный момент времени известно положение МЦС фигуры. Тогда, принимая его за полюс и учитывая, что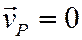 
, получим по формуле (4) для произвольной точки фигуры
т.е. знание МЦС упрощает определение скоростей точек плоской фигуры, т.к. сразу позволяет определить модуль скорости по формуле (5) и направление: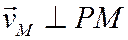 
.
Таким образом, при известном МЦС вектор скорости любой точки плоской фигуры равен
модуль определяется по формуле
направлен вектор к отрезку РМ, соединяющему МЦС с данной точкой М, в сторону вращения фигуры вокруг МЦС.
В силу вышесказанного, возникает важная задача об определении положения МЦС плоской фигуры.
Положение мгновенного центра скоростей плоской фигуры может быть найдено, если:
1) задан закон движения (1) плоской фигуры (МЦС определяется с помощью дифференциальных равенств);
2) известны направления скоростей двух точек плоской фигуры, или их траектории.
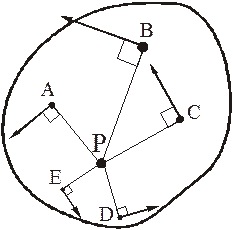
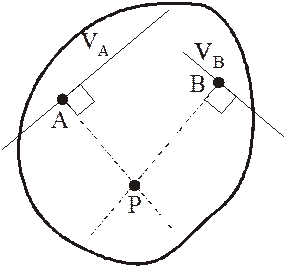
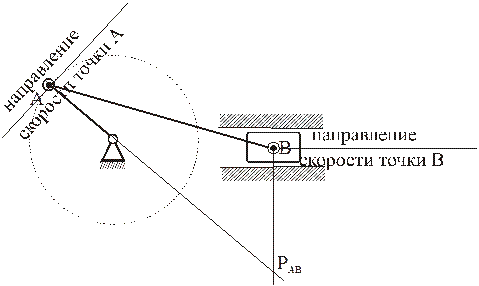
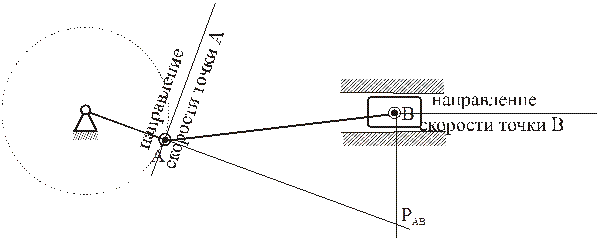
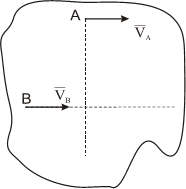
Рассмотрим только случай 2). Пусть известны направления скоростей двух точек А и В фигуры. Тогда для нахождения МЦС надо из этих точек опустить перпендикуляры к направлениям скоростей. В точке пересечения этих перпендикуляров и будет МЦС.
Частные случаи определения МЦС.
а) скорости точек параллельны, но точки не лежат на общем перпендикуляре к скоростям
Ясно, что в этом случае перпендикуляры к скоростям параллельны,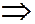 
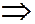
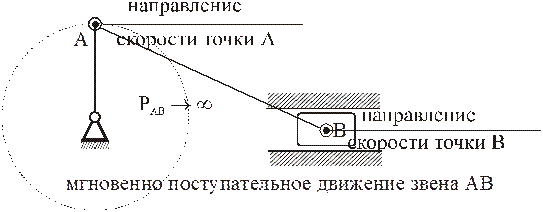
пересекаются в ¥, угловая скорость фигуры = 0 и скорости всех её точек в данный момент равны между собой. Такое движение фигуры называют мгновенно поступательным.
Замечание. Не путать мгновенно поступательное движение с поступательным: при поступательном движении скорости и ускорения всех точек равны между собой в любой момент времени, а при мгновенно поступательном равны только скорости всех точек (но не ускорения – они не равны друг другу!) и только в данный момент.
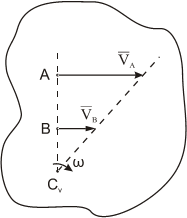
б) скорости двух точек фигуры параллельны, направлены в одну сторону и их модули не равны друг другу, а точки лежат на одном перпендикуляре к скоростям
В этом случае одних направлений скоростей не достаточно: должны быть известны и их модули.
Для нахождения МЦС надо концы векторов скоростей соединить прямой линией: в точке её пересечения с продолжением отрезка АВ и будет МЦС.
Если известно расстояние АВ, то легко получить
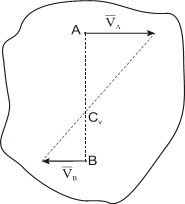
в) то же, что и в предыдущем случае, но векторы скоростей направлены в разные стороны; в этом случае модули скоростей могут быть и равны между собой, но должны быть известны.
Нахождение МЦС также аналогично предыдущему: концы векторов скоростей соединяем прямой линией – в точке её пересечения с отрезком АВ будет МЦС.
Если задано расстояние АВ, то аналогично пункту б) можно найти
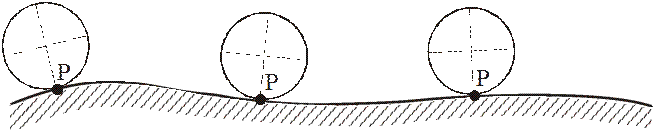
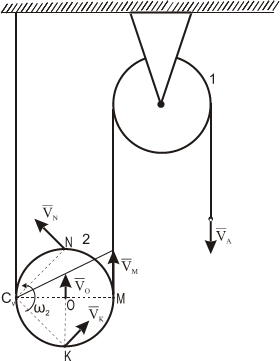
г) качение колеса без скольжения по любой гладкой неподвижной поверхности.
Если колесо всё время остаётся в вертикальной плоскости, и отсутствуют повороты вокруг вертикальной оси, то оно совершает плоскопараллельное движение. В этом случае положение МЦС сразу известно: в точке контакта колеса с поверхностью. Действительно, если нет скольжения, то скорость точки контакта равна скорости соответствующей точки поверхности, т.е. нулю (поверхность неподвижна). По определению МЦС – здесь он и находится.
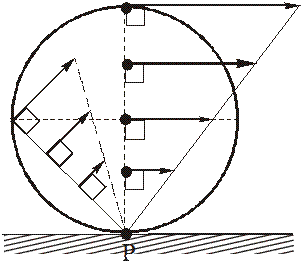
В связи с этим, интересно посмотреть распределение скоростей точек катящегося без скольжения колеса:
скорость верхней точки колеса в два раза больше скорости его центра!
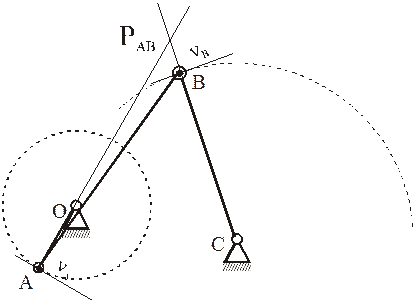
Примеры определения МЦС для шатуна АВ кривошипно-ползунного механизма.
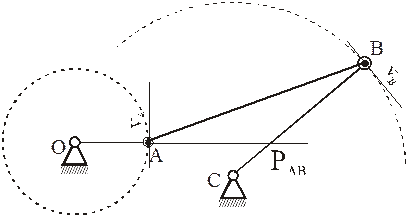
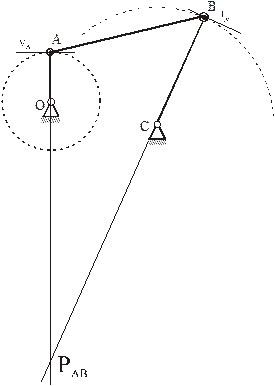
Определение МЦС для шатуна АВ кривошипно-коромыслового механизма:
Рассмотрим пример определения скорости и ускорения точки плоской фигуры.
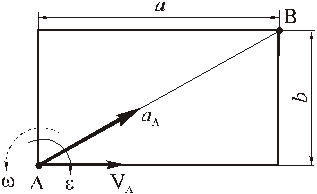
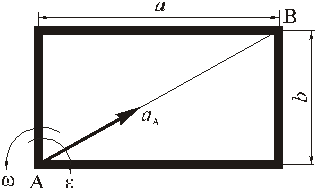
Прямоугольная пластина со сторонами a = 0,4 м и b = 0,3 м движется в своей плоскости. В данный момент времени скорость точки А пластины равна по модулю vA = 4 м/с, модуль ускорения этой точки равен aA = 3 м/с 2 , модули угловой скорости и углового ускорения фигуры равны соответственно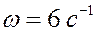 
, 
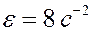
. Направления показаны на рисунке.
Определить скорость и ускорение точки B плоской фигуры в этот момент времени.
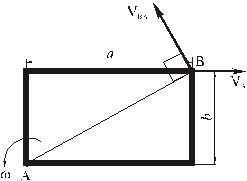
РЕШЕНИЕ. Принимая за полюс точку А, для определения скорости точки B используем формулу (4):
Вычислив расстояние АВ
по формуле (5) найдём модуль скорости точки В при её вращении вокруг полюса А
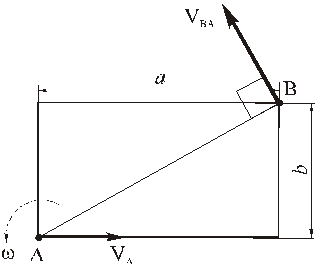
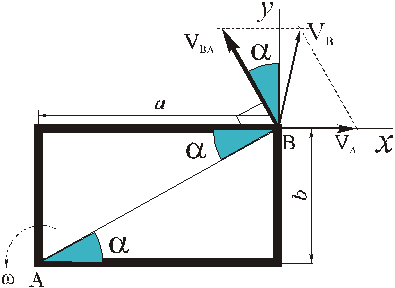
Изображаем вектор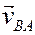 
(
):
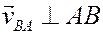
(стрелка вектора 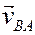должна быть направлена в сторону вращения фигуры!).
Вектор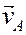 
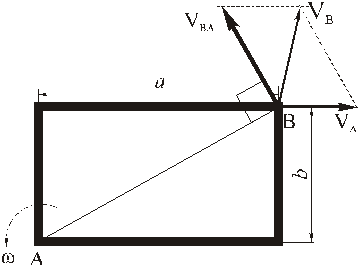
скорости полюса переносим параллельно в точку В,
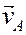
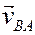
согласно равенству (4) складываем векторы и .
Для определения модуля скорости находим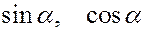 
:
Теперь модуль скорости можно найти двумя способами:
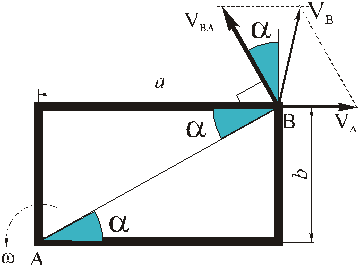
по теореме косинусов (формула (6))
При определении скорости вторым способом выбираем оси координат
и проектируем (4) на эти оси:
Ускорение точки В определяем по формуле (8)
принимая за полюс точку А с известным ускорением.
По формулам (10) и (12) находим модули ускорений
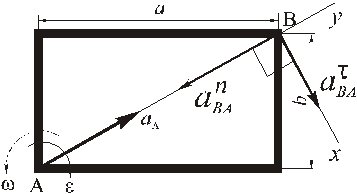
Изображаем векторы этих ускорений:
.
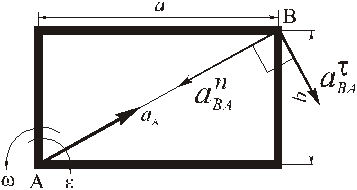
Так как согласно (8) для определения вектора ускорения точки В надо складывать три вектора, то выбираем оси координат
и проектируем (8) на эти оси:
Модуль ускорения будет
Геометрически (на рисунке) вектор ускорения строится при помощи «векторного многоугольника»: от заданной точки в выбранном масштабе последовательно откладываются векторы так, что конец предыдущего вектора является началом следующего; сумма векторов – вектор, идущий из заданной точки в конец последнего вектора.
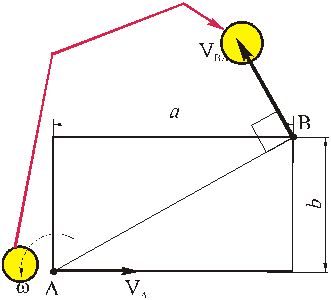
Зная скорость точки А и угловую скорость фигуры можно найти положение мгновенного центра скоростей. Из равенства (15) следует
Используя доказательство существования МЦС, получаем.
Источник
iSopromat.ru
Мгновенным центром скоростей (МЦС) при плоскопараллельном движении называют связанную с плоской фигурой точку, скорость которой в данный момент равна нулю.
Такая точка существует в каждый момент времени.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
Рис. 1.5 т C — Мгновенный центр скоростей
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс.
Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.
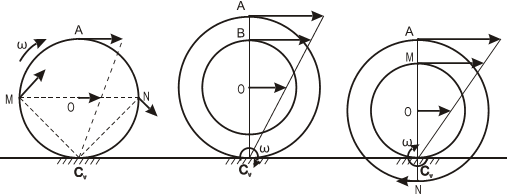
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
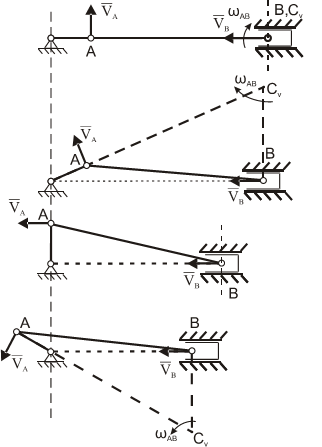
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
- СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
- МЦС лежит в «бесконечности»
В этом случае МЦС находится в “бесконечности”, т.е
Формулы справедливы при отсутствии проскальзывания в точке СV.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Набор студента для учёбы
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Источник
