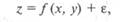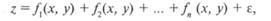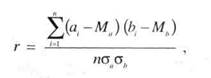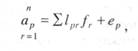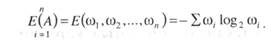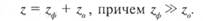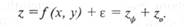Способ математико картографического моделирования

Математико-картографическое моделирование (МКМ). Элементарные математико-картографические модели

2.2.4. Математико-картографическое моделирование

Математико-картографическое моделирование (МКМ) сформировалось из многочисленных отдельных экспериментов по применению математических методов в тематической картографии в начале 70-х годов XX в. [В.Т.Жуков, С.Н.Сербенюк, В.С.Тикунов, 1973; 1980]. Под математико-картографическим моделированием понимается органическое комплексирование математических и картографических моделей в системе «создание — использование карт» для конструирования или анализа тематического содержания карт. Математико-картографические модели могут быть элементарными, выражающимися следующим образом:

исходные данные + математическая модель = результат моделирования.

Под словом «данные» могут пониматься сведения, считанные с карты, или результатом моделирования будет тематическое содержание карты. Иными словами, либо на начальном этапе моделирования, либо на конечном, или сразу на этих двух этапах должна присутствовать картографическая модель, в противном случае такое моделирование уже нельзя будет назвать математико-картографическим.
Прежде всего несколько слов следует сказать о составных компонентах математико-картографического моделирования — картографических и математических моделях. Что касается карты, то она представляет собой математически строго определенную формализованную модель, построение которой производится по канонам математической картографии. Моделируемая действительность на карте, как и в математической модели, передается в условной знаковой форме, но карта обладает свойством, отличающим ее от математической и любой другой модели, она визуализирует территориальную конкретность. Именно это свойство обусловливает образную наглядность картографических характеристик территории и объясняет многовековую традицию и разнообразие направлений использования карт в науке и на практике. Карта не только абстрактная знаковая, но также аналоговая модель действительности. Доказательством тому служат многообразие приемов передачи характеристики явлений посредством взаимозаменяемых способов картографического изображения, а также однозначность характеристики конкретных территориальных свойств географической действительности.
Несмотря на различия математической и картографической моделей именно математика послужила одной из важных причин возникновения и развития таких способов изображения, как картограмма или картодиаграмма, точечный или изолиний. Не являются редкостью и приемы математической статистики, издавна используемые в картосоставительской практике при проведении отбора объектов картографирования, построении шкал по количественным признакам, обобщении статистических данных и т. п. Новым для картографии явился углубляющийся процесс внедрения математических методов в формирование тематики и содержания карт, приводящий к более глубокой перестройке методики их создания [В.Т.Жуков, С.Н.Сербенюк, В.С.Тикунов, 1980]. Все это позволяет говорить о возможности органического комплексирования математических и картографических моделей и нецелесообразности их противопоставления, хотя в литературе можно встретить утверждение о превосходстве одной формы моделирования над Другой как в одну, так и другую сторону [Геология. 1967; Л.Л.Ягодина, 1973, В.А.Анучин, 1982 и др.]. В качестве объектов для критики чаще всего используются примеры математического описания пространственных явлений, не имеющих даже сколь-либо глубоко разработанных логических определений. Но ведь совершенно недопустимо математическими формулами описывать то, что еще логически не осмыслено и не представлено в виде, пригодном для математического описания. Критика картографической составляющей направлена на то, что она менее точно по сравнению с математическими моделями описывает явления и др.
Обе отмеченные взаимоисключающие позиции имеют определенную почву под собой. Прежде всего этому способствовали ряд достигнутых успехов на пути математизации, внедрение этих разработок в практику, широкое распространение компьютеров и другие причины, а также упрощенное описание сложных пространственно распределенных явлений без достаточного понимания их сути, применение математических алгоритмов без учета накладываемых ими ограничений, игнорирование методов, традиционных для наук о Земле, и т.д. Иногда требовалось просто невозможное как, например, решение задачи всесторонней математической имитации сложных комплексов с учетом большого числа взаимосвязей между отдельными их компонентами и т.п. Стоит ли в этих случаях применять модели? Нет. Явление во всем его многообразии лучше изучать в натуре, чем на модели. Модель ведет к упрощениям (в разумных рамках), позволяет выявить главные типичные черты, а тем самым дает и новое знание о явлении — и в этом ее сила. Любому моделированию свойственны формалистичность построений и стремление использовать ее сильные стороны. Не подмена одних методов другими, а их взаимное дополнение с учетом сильных сторон математического и картографического методов — наиболее рациональный путь.
Сочетание математических и картографических моделей может быть самым разнообразным и выражаться как в простых формах, так и в виде сложного многостадийного процесса. Последний строится как бы из этих моделей-звеньев, которые могут быть классифицированы [В.С.Тикунов, 1979]. Математико-картографическая модель как бы синтезирует математический и картографический элементы вместе. В связи с этим отпадает необходимость классифицировать элементарные математико-картографические модели по типам применяемых в них карт или по математическому аппарату.
Такая классификация особенно интересна, поскольку и в картографии, и в математике уже существуют их деление и соответственно классификации.

В нашем случае ни картографическая, ни математическая компоненты по отдельности не определяют вид МКМ. Образно говоря, математический аппарат подобен мясорубке, которая лишь перекручивает, перерабатывает данные и представляет их в более удобном для анализа виде, вскрывает затушеванные закономерности и т.д., чаще всего фиксируемые на картах. Основываясь на данных положениях, была разработана классификация элементарных математико-картографических моделей.
A. Модели структуры явлений.
I. Модели структуры пространственных характеристик явлений.
II. Модели структуры содержательных характеристик явлений.
B. Модели взаимосвязей явлений.
I. Модели взаимосвязей пространственных характеристик явлений.
II. Модели взаимосвязей содержательных характеристик явлений.
C. Модели динамики распространения (развития) явлений.
I. Модели динамики пространственного распространения явлений.
II. Модели динамики содержательного развития явлений.

Несмотря на различие моделей пространственных и содержательных характеристик, здесь нет разрыва диалектического единства пространства и содержания, но в одном случае на первый план больше выступает первое свойство, а в другом — второе. Обратимся к конкретным примерам конструирования элементарных моделей. Это позволяет уяснить необходимость подразделения моделей структуры, взаимосвязей и динамики на два подвида. Например, создание моделей потенциала поля расселения, равномерности размещения населенных пунктов, аппроксимации статистических поверхностей (модели структуры); модели согласованности контуров объектов между собой, корреляции пространственного варьирования характеристик двух явлений (модели взаимосвязей); модели пространственного распространения эпидемий или диффузии загрязнения, миграций населения (модели динамики) невозможно осуществить без учета в процессе математической формализации пространственного аспекта, без привлечения пространственных координат, фиксирующих положение явлений. Необходимость использования пространственных координат явлений заложена в строении данных алгоритмов.
С другой стороны, при многомерной группировке территориальных единиц по комплексу показателей в однородные группы (модели структуры); при моделировании соответствия распределения занятых в отраслях хозяйства по стране в целом и по единицам ее административного деления (модели взаимосвязей); при прогнозировании роста городов по данным за ряд предыдущих лет (модели динамики) сведения о пространственном положении явлений в процессе математического моделирования не учитываются. Ставится задача проанализировать структуру, взаимосвязи или динамику явлений любой территориальной единицы по сравнению с другими, вне зависимости от того, где они расположены. Однако зачастую результаты математического моделирования содержательных характеристик явлений наносятся на карту, что придает им пространственную определенность. Это позволяет анализировать полученные результаты по отношению друг к другу в пространстве и дает им дополнительные преимущества перед другими формами представления результатов моделирования, например таблицами, списками, что также часто встречается в географии и экологии. Примеры конструирования элементарных моделей всех пунктов приведенной классификации представлены в работе [В.С.Тикунов, 1985; 1997].

Источник

Приемы математико-картографического моделирования

Формализованное картографическое изображение хорошо при­способлено для математического анализа. Как упоминалось выше, каждой точке карты с координатами х и у поставлено в соответ­ствие лишь одно значение картографируемого параметра г, что позволяет представить изображение данного явления как функ­цию z — F(x,y). В других случаях картографическое изображение удобно представить как поле случайных величин и воспользовать­ся для его анализа вероятностно-статистическими методами.

В принципе почти все разделы математики применимы для обработки и анализа картографического изображения. Проблема лишь в том, чтобы точно подобрать математическую модель и, главное, дать надежное содержательное истолкование результатам моделирования. Достаточно прочно в картографический анализ вошли некоторые разделы численного анализа, многомерной ста­тистики, теории вероятностей и теории информации.

Аппроксимации. Под аппроксимациями в математике понимают замену (приближение) сложных или неизвестных функций другими, более простыми функциями, свойства которых известны. Любую слож­ную поверхность (поле), изображенную на изолинейной карте, можно аппроксимировать, т.е. приближенно представить в виде

где/(f у) — некая аппроксимирующая функция, е — остаток, не поддающийся аппроксимации. Функцию/(х, у) можно далее раз­ложить в ряд, представив уравнение поверхности в виде

где/(f, у) — компоненты разложения, которые предстоит опреде-

лить. В общем случае для этого с аппроксимируемой карты снимают ряд значений z_n после чего составляют систему уравнений, решае­мых совместно по способу наименьших квадратов, т.е. так, чтобы

Существуют разные способы аппроксимации. Это обычные ал­гебраические многочлены, ортогональные многочлены Чебышева и Лежандра, которые определенным образом упрощают вычисле­ния, сплайн-функции и др. Не останавливаясь на особенностях математического аппарата, отметим, что во всех случаях задача сводится к тому, чтобы аппроксимирующее уравнение наилучшим образом описывало исходную поверхность, а сумма квадратов от­клонений I е. 2 была бы минимальна.

На рис. 12.16 показано последовательное улучшение аппрок­симаций на примере несложных поверхностей. Аппроксимация 1-го порядка (линейное уравнение) дает плоскость, отражающую только общий уклон поверхности, это очень грубое, слишком общее приближение. Поверхность 2-го порядка уже больше похо­жа на исходную модель, а аппроксимация 3-го порядка (кубичес­кое уравнение) дает достаточно хорошее приближение к исход­ной поверхности.

Тригонометрические функции позволяют описывать сложные, сильно расчлененные поверхности, а сферические функции при­меняют, если при вычислениях нельзя пренебречь кривизной зем­ной поверхности. Аппроксимация с помощью двойных рядов Фу­рье, представленная на рис 12.17, иллюстрирует постепенное ус­ложнение поверхности за счет добавления двухмерных синусоид с разными фазами и амплитудами. Компьютерное моделирование позволяет выполнять подобные аппроксимации для поверхностей любой сложности, вычисляя уравнения высокого порядка, содер­жащие порой несколько десятков членов разложения.

В исследовательской практике аппроксимации используют для аналитического описания поверхностей (полей), изображенных на картах, и выполнения с ними различных действий: суммиро­вания, вычитания, интегрирования и дифференцирования, для подсчета объемов тел, ограниченных этими поверхностями, и ре­шения множества других задач. Одно из направлений использова­ния аппроксимаций — разложение поверхностей на составляю­щие, что позволяет выделять и анализировать нормальные и ано­мальные факторы развития и пространственного размещения явлений (см. разд. 13.2).

230 Глава XII Методы использования карт

Приемы математико-картографического моделирования 231

Рис. 12.16.Аппроксимации поверхностей:

а — блок-диаграмма исходной поверхности; б, в, г — блок-диаграммы аппрок­симирующих поверхностей соответственно I, 2 и 3-го порядков.

Рис. 12.17.Схема тригонометрической аппроксимации поверхности с по­мощью последовательного наложения двухмерных синусоидальных волн (по Дж. Дэвису).

Приемы математической статистики. Эта группа приемов мате­матико-картографического моделирования предназначена для изу­чения по картам пространственных и временных статистических совокупностей и образуемых ими статистических поверхностей.

232 Глава XII. Методы использования карт

Приемы математико-картографического моделирования 233

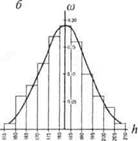
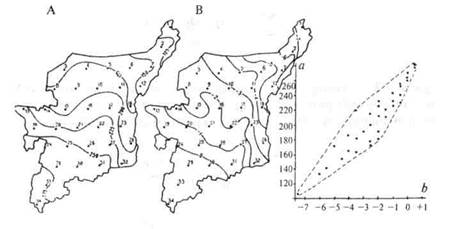
Рис. 12.18.Фрагмент карты рельефа (а) с сеткой точек регулярной вы­борки (выходы сетки отмечены на рамке), гистограмма и кривая рас­пределения высот (б): со — частость; h — высоты рельефа.

Статистический анализ картографического изображения пре­следует главным образом три цели:

♦ изучение характеристик и функций распределения явления;

♦ изучение формы и тесноты связей между явлениями;

♦ оценка степени влияния отдельных факторов на изучаемое явление и выделение ведущих факторов.

В основу всякого статистического исследования кладется вы­борка, т.е. некоторое подмножество однородных величин я., сня­тых с карты по регулярной сетке точек (систематическая выбор­ка), в случайно расположенных точках (случайная выборка), на ключевых участках (ключевая выборка) или по районам (райони­рованная выборка).

Выборочные данные группируют по интервалам, составляют гистограммы распределения (рис. 12.18) и затем вычисляют раз­личные статистики — количественные показатели, характеризу­ющие пространственное распределение изучаемого явления. Наи­более употребительные показатели — среднее арифметическое, среднее взвешенное арифметическое, среднее квадратическое, дис-

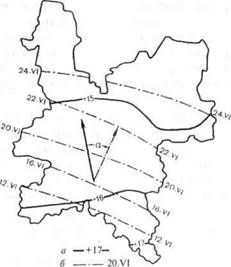
Рис. 12.19.Карты явлений и поле корреляции.

А — карта испарения с суши (мм/год) для территории Республики Коми; В — карта средней годовой температуры воздуха (°С) для той же территории.

персия, вариация и др. Кроме того, с помощью специальных по­казателей (критериев согласия) можно оценить соответствие дан­ного конкретного распределения тому или иному теоретическому закону распределения. Например, установить, согласуется ли эм­пирическое распределение высот рельефа с кривой нормального распределения, как это видно на рис. 12.18, или подчиняется ка­кой-то иной функции.

Другая типичная исследовательская задача — оценка взаимо­связи между явлениями — решается с помощью хорошо разрабо­танного в математической статистике аппарата теории корреляции. Для этого необходимо иметь выборки по сравниваемым явлени­ям, показанным на картах разной тематики (например, А и В). Значения а. и Ь. берут в одних и тех же /-х точках, т.е. строго скоор­динировано, и затем строят график поля корреляции (рис. 12.19).

Если поле корреляции может быть аппроксимировано прямой, которая называется линией регрессии, то приступают к вычисле­нию коэффициента парной корреляции г. Его числовые значения заключены в интервале +1 > г > — 1. При г равном +1 или —1 существует функциональная прямая или обратная связь. Если г близок к 0, то связь между явлениями отсутствует, а при г > |0,7| связь считается существенной. Коэффициент корреляции рассчи­тывают по формуле

234 Глава XII. Методы использования карт

Приемы математико-картографического моделирования 235

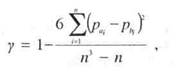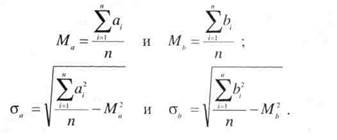где а. и Ь. — выборочные данные, полученные по картам А и В; п — объем выборки (число пар данных); М_а и М_ь — соответствую­щие значения средних, а о_аи о_ь — средних квадратических.

236 Глава XII. Методы использования карт

где р_а. и p_h. — ранги значений, полученных соответственно по кар­там А и В, т.е. их порядковые номера в возрастающей последова­тельности (1, 2, 3 и т.д.), an — объем выборки.

По смыслу у аналогичен коэффициенту парной корреляции г, он изменяется в интервале от —1 до +1. При этом не требуется больших объемов выборки, расчеты можно выполнять даже при п = 3. К тому же не нужны точные количественные значения й и Ь_р достаточно знать их ранги. Все это удобно для работы с картог­раммами, где используются интервальные шкалы, а объем выбор­ки ограничен числом административных районов.

Аппарат теории корреляции достаточно разнообразен, в нем есть показатели, удобные для анализа взаимосвязей по картам аре­алов (где явления характеризуются только двумя состояниями: «есть» и «нет»), по картам качественного фона (где каждое явле­ние имеет много состояний, но не охарактеризовано количествен­но). Существуют коэффициенты для расчета криволинейных зави­симостей и связей между тремя явлениями (коэффициенты мно­жественной корреляции) и т.п.

Расчет корреляций дает основу для более сложных видов ана­лиза: регрессионного, дисперсионного, факторного и др. Часто при исследованиях ставится задача выделить основные факторы, опре­деляющие развитие и размещение того или иного явления. Эту задачу решает многомерный факторный анализ. Он позволяет све­сти к минимуму (к трем-четырем главным факторам) большие совокупности исходных показателей, характеризующих сложное явление. Уравнение факторного анализа имеет вид

где а — исходные показатели;^ — выделенные главные факторы, дающие синтетическую оценку изучаемого явления; / — «вес» каждого фактора в этой синтетической оценке («факторная на­грузка»); е_р — остаток, характеризующий неучтенные отклонения.

Приемы теории информации. Эти приемы используют для оцен­ки степени однородности и взаимного соответствия явлений, изу­чаемых по картам.

Речь идет об основной функции теории информации — энтро­пии. В термодинамике энтропия характеризует степень беспорядка в физической системе, в теории связи — степень неопределенности

Приемы математико-картографинеского моделирования 237

передаваемых сообщений, а в картографическом анализе эта функ­ция оказалась довольно удобной для оценки степени однородности/ неоднородности (разнообразия) картографического изображения.

Энтропией Е (А) некоторой системы А называется сумма про­изведений вероятностей со_/ различных состояний этой системы на логарифмы вероятностей, взятая с обратным знаком

В теории информации принято брать логарифмы вероятностей при основании 2, что связано с двоичной системой счисления. Смысл функции не изменится, если пользоваться десятичными или натуральными логарифмами. Функция Е(А) остается неотри­цательной, она обращается в нуль, когда на карте изображен только один контур или выдел (т.е. изображение совершенно однородно), и монотонно возрастает с увеличением числа контуров п. Это свой­ство функции энтропии позволяет количественно характеризовать неоднородность картографического изображения (рис. 12.21), по­нимаемую как разнообразие контуров и неравномерность их рас­пространения по площади (различие величин со,.).

Рис. 12.21.Увеличение энтропии Е<А) с возрастанием числа контуров на карте (а) и изменением соотношения их площадей (б).

Кроме того, информационные функции используют для оценки степени взаимного соответствия (совпадения) контуров на разных картах. В этом случае они выполняют роль своеобразных показателей взаимосвязи явлений наподобие коэффициентов корреляции.

Изучение структуры 239

Глава XIII

Исследования по картам

Способы работы с картами

Рассмотренные в предыдущей главе технические приемы исполь­зуют для работы с отдельными картами либо с сериями карт и ком­плексными атласами. Исследования по картам выполняют для опре­деления размещения и пространственно-временной структуры яв­лений и процессов, их взаимных соотношений и связей, выявления тенденций развития и динамики, для получения всевозможных ко­личественных характеристик и оценок, проведения районирования и классификаций, прогноза изменений во времени и пространстве.

Способы работы с картами подразделяют следующим образом.

Анализ отдельной карты

♦ Изучение картографического изображения без его преобра­зования, т.е. анализ карты в том виде, в каком она есть.

♦ Преобразование картографического изображения с целью приведения его в вид, более удобный для данного конкрет­ного исследования.

♦ Разложение картографического изображения на составляю­щие — особый вид преобразования, применяемый для выде­ления нормальной и аномальной (фоновой и остаточной) компонент развития и размещения явлений и процессов.

Анализ серий карт

♦ Сравнение карт разной тематики с целью установления вза­имосвязей и зависимостей между явлениями.

♦ Сопоставление разновременных карт для изучения динамики и эволюции явлений и процессов, составления прогнозов их развития во времени.

♦ Изучение карт-аналогов для обнаружения общих закономер­ностей распространения явлений и процессов на разных тер­риториях.

Исследования по картам, как и любые другие, включают не­сколько этапов:

♦ постановка задачи — формулирование цели, выделение под­задач, определение требований к точности;

♦ подготовка к исследованию — выбор картографических ис­точников, методов, технических средств, алгоритмов и т.п.;

♦ собственно исследование — получение предварительных, а затем окончательных результатов, их оценка, создание но­вых карт;

♦ интерпретация результатов — содержательный анализ, фор­мулирование выводов и рекомендаций, оценка их надеж­ности.

Исследования по картам — это всегда более или менее форма­лизованная процедура. На всех этапах ей должны сопутствовать содержательный географический анализ получаемых результатов, соотнесение их с реальной ситуацией и, если необходимо, кор­ректировка самой процедуры исследования.

Изучение структуры

Изучение по картам структуры явлений и процессов — это выявление и анализ их элементов, размещения в пространстве, конфигурации, порядка (уровня) и иерархии. Конечная цель ис­следования всегда состоит в познании пространственной органи­зации геосистем, их генезиса, в раскрытии механизма функцио­нирования.

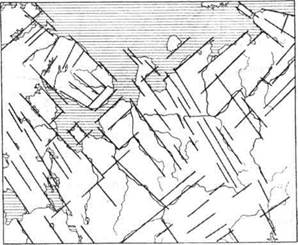
Один из наиболее информативных способов изучения структу­ры — анализ конфигурации картографических образов, т.е. изучение геометрического рисунка изображения. По внешнему облику объекта часто можно судить о его морфологии, генезисе, о факторах, сфор­мировавших тот или иной объект. На рис. 13.1 показаны некоторые типичные конфигурации географических объектов, по которым можно сделать предположения об их генезисе. Так, параллельный рисунок гидрографической сети, скорее всего, свидетельствует о системе трещиноватости того же простирания, которой подчине­ны речные долины, а радиальное растекание водотоков — о купо­лообразном тектоническом поднятии. Древовидная конфигурация почвенных контуров означает их приуроченность к долинам рек, а

240 Глава XIII. Исследования по картам

Рис. 13.1. Типичные конфигурации объектов на тематических картах при­роды.

а — параллельный рисунок (гидросеть Приобского плато); б — древовидный рисунок (почвенные ареалы в долине р. Игрит); в — решетчатый рисунок (разломы в Предбайкалье); г — веерный рисунок (разрывные нарушения в Восточном Саяне); д — веерный рисунок (дельта р. Селенги); е — радиаль­ный рисунок (речная сеть на Путоранском сводовом поднятии); ж — дугооб­разный рисунок (пойменные гривы в излучине р. Вилюй); з — кольцевой рисунок (тектонические структуры в Казахстане); и — пятнистый рисунок (пятна талых и мерзлых пород в Якутии).

веерный рисунок характерен для природных объектов, формиру­ющихся на дельтах, и т.д.

Картографический метод позволяет эффективно выявлять про­странственные закономерности и аномалии, т.е. типичные, устой­чивые, широко распространенные структуры и отклонения от них. Карты, обладающие большой обзорностью, как бы специально предназначены для выявления общих закономерностей глобаль-

Рис. 13.2.Основные линеаменты северо-западного и северо-восточного простираний, выявляемые по физической карте Севера Русской рав­нины.

ного и регионального уровней. В значительной степени этому спо­собствует и генерализация, освобождающая изображение от мело­чей, деталей и выпукло проявляющая главные, наиболее суще­ственные его черты.

Напомним, что именно благодаря обзорности карт были уста­новлены такие важнейшие закономерности географической струк­туры, как зональность, сеть планетарных линеаментов, единая система срединно-океанических хребтов и рифтовых зон, струк­тура центральных мест и т.п. Глобальные системы линеаментов можно обнаружить при внимательном анализе карт любого масш­таба. На карте Севера Русской равнины (рис. 13.2) отчетливо про­явлена система северо-западных и северо-восточных линеаментов. Им подчиняются береговые линии морей и озер, направления водоразделов и речных долин. Таковы очертания Кольского полу­острова, берега Белого и Печорского морей, вытянутые озера Карелии, долины рек Северной Двины, Онеги, Мезени, Вашки, Сухоны, Вычегды, Печоры, Усы, Тиманский кряж, Северный Урал, хребет Пай-Хой и другие крупные оро- и гидрографичес­кие элементы. Все это — отражение системы трещиноватости,

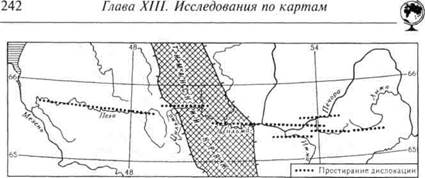
Рис. 13.3.Речная сеть в районе Транстиманской дислокации. Точечным пунктиром показано простирание дислокации.

охватывающей всю планету и обязанной своим происхождением ротационным напряжениям, возникающим на земном шаре. Ин­тересно, что аналогичные системы северо-западных и северо-вос­точных линеаментов можно видеть и на картах других планет зем­ной группы. Это общая закономерность планетарного рельефа.

На фоне закономерностей нередко удается подметить анома­лии, и глаз опытного исследователя сравнительно легко их рас­познает. В качестве иллюстрации на рис. 13.3 показана уникальная для Севера Русской равнины широтная орографическая аномалия в полосе между 65° и 66° с.ш. Словно глубокая борозда прорезает Тиманский кряж, и в ней расположены долин рек Пезы, Циль-мы, Печоры. Она аномальна по отношению к господствующим здесь северо-западным линеаментам. Так проявлена в рельефе глу­бинная Транстиманская тектоническая дислокация.

Изучая структуру явлений, часто стараются выявить основные и второстепенные компоненты. Отделить аномалии от фона помо­гает операция разложения картографического изображения на со-ставляющие, которую можно выполнить с помощью усреднения, аппроксимации или фильтрации. В задаче о разложении принима­ется, что показанное на карте явление z представляет собой ре­зультат совокупного влияния основного, наиболее значительно­го, фонового фактора £., зависящего от причин регионального, а иногда даже глобального масштаба, и дополнительных факторов, накладывающихся на общий фон и усложняющих картину, — их называют остаточными i_o или аномальными

Рис. 13.4.Графическое разложение поверхности на составляющие.

о — гексагональная сетка, по которой осуществляется усреднение; б — ис­ходная поверхность с отметками высот; в — усредненная фоновая поверх­ность с осредненными значениями высот; г — остаточная поверхность с ве­личинами отклонений исходной поверхности от фоновой.

Примерами могут служить ареалы повышенного радиационно­го загрязнения на фоне допустимых значений, локальные подня­тия и опускания на фоне региональных тектонических движений, местные климатические особенности, накладывающиеся на зональ­ные закономерности, и т.п.

Самый простой способ разложения — графическое осреднение. Для этого на исходной карте размещают сетку регулярных точек так, как показано на рис. 13.4, в центре каждой шестиугольной ячейки вычисляют значение скользящего среднего ц как среднего из значений вершин и центра ячейки: 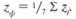На изолинейной

карте, построенной по значениям z_(/p отражена осредненная фоно­вая поверхность (рис. 13.4в),передающая главные, наиболее круп­ные черты структуры. Если далее в каждой точке взять разности между фактическим и осредненным значениями 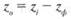и про-

вести по ним изолинии, то получится остаточная поверхность, показывающая размещение аномалий, отклонений, второстепен­ных деталей (рис. 14.4г).

16*

244 Глава XIII. Исследования по картам

А б в

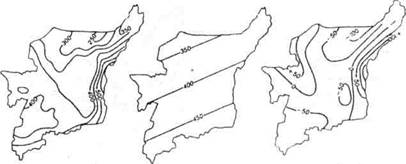
Рис. 13.5.Карта осадков теплого периода (в мм) на территории Республи­ки Коми (а) и карты фоновой (б) и остаточной (в) поверхностей, полученные в результате аппроксимации уравнением 1-го проядка.

Аналогичный эффект разложения на составляющие достигает­ся и при расчете аппроксимирующей поверхности и отклонений от нее фактической исходной поверхности. При этом предполага­ется, что фоновая составляющая описывается некоторой неслу­чайной функцией/(х, у), а неучтенные отклонения от нее е соот­ветствуют остаточной поверхности. Иначе говоря, члены аппрок­симирующего уравнения приравниваются к членам уравнения разложения на составляющие

На рис. 13.5 представлена карта осадков теплого периода года на территории Республики Коми и результаты ее разложения на фоновую поверхность 1 -го порядка и остаточную поверхность. Карта фоновой поверхности передает общее увеличение количества осад­ков в направлении на юго-восток, что может быть связано с трансформацией масс арктического воздуха по мере их продвиже­ния в глубь материка. А карта остаточной поверхности показывает отклонения от этой закономерности, в частности резкое увеличе­ние количества осадков на западных склонах Урала и в районе Тиманского кряжа.

Углубленное изучение структуры явлений нередко требует пре­образования картографического изображения, т.е. трансформиро­вания его с целью создания производных карт и получения по ним новой информации. Различают несколько видов преобразования.

Рис. 13.6.Схематизация. Преобразование карты современного рельефа в карту морфоизогипс: а — современный рельеф; б — восстановлен­ный «первичный» рельеф; точечным пунктиром показано обобще­ние некоторых горизонталей.

Вычленение, т.е. выделение на карте интересующих исследова­теля компонентов сложной геосистемы и снятие прочих деталей. Выделенные элементы предстают в наглядной иудобной для дан­ного исследования форме, например в виде системы спрямленных элементов рельефа и гидрографии, как на рис. 13.2.

Схематизация — устранение второстепенных деталей и пред­ставление картографического изображения в упрощенном виде. Так, при схематизации гипсометрического изображения и снятии дета­лей эрозионного расчленения проявляется основная первично-тек­тоническая структура рельефа (рис. 13.6).

Детализация — преобразование, противоположное схематиза­ции, оно имеет целью сделать изображение более подробным. На­пример, на топографической карте можно детализировать изобра­жение эрозионной сети, проведя по изгибам горизонталей тальве­ги временных водотоков.

Континуализация — замена дискретного картографического изображения непрерывным, что обычно связано с введением по­нятия «географическое поле». Например, карту тектонических тре­щин преобразуют в псевдоизолинейную карту поля трещинова-

Глава XIII. Исследования по картам

Рис. 13.7.Континуализация.

а — преобразование карты трещин широтного простирания в карту поля трещиноватости (км/км 2 ); б — преобразование карты размещения тетереви­ных птиц в карту их плотности; значками показано число птиц, а на изоли-нейной карте — их плотность на 1 км 2 .

тости (рис. 13.7), карту расселения — в карту плотности населе­ния, карту размещения лесов — в карту лесистости и т.п. Такие преобразования дают представление об абстрактном рельефе явле­ния, на производных картах хорошо читаются максимумы и ми­нимумы распределения, их удобно коррелировать с другими изо-линейными картами.

Дискретизация — обратное преобразование, имеющее целью перевод непрерывного изображения в дискретную форму. Хоро­шим примером может служить интерполирование по сетке точек при создании цифровых моделей по картам с изолиниями или картограммам.

Средствами подобных преобразований часто служат графичес­кие операторы— сетки равномерно или неравномерно располо­женных точек, геометрических ячеек, в каждой из которых выпол-

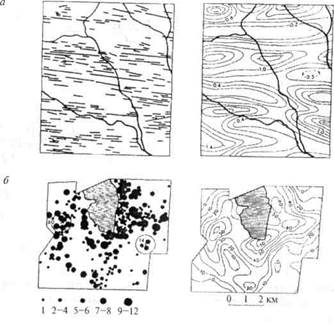
Рис. 13.8. Операторы (сетки и палетки), применяемые для преобразова­ния картографического изображения.

а — регулярные неперекрывающиеся операторы: 1 — квадратная сетка; 2 — гексагональная сетка; 3 — радиально-концентрическая палетка; б — регуляр­ные перекрывающиеся (скользящие) операторы: 4 — скользящие кружки; 5 — перекрывающиеся шестиугольники; в — нерегулярные операторы: 6 — случайно выбранные квадраты; 7 — избирательно взятые кружки.

няют пересчет исходных данных и получают производные показа­тели. Если ячейки (квадраты, кружки и др.) перекрываются по площади, то их называют скользящими операторами. Примеры наи­более типичных операторов показаны на рис. 13.8.

Преобразования подразделяют на однократные и многократ­ные. В свою очередь, многократные преобразования бывают парал­лельными и последовательными. При параллельных преобразова­ниях по исходной карте А получают сразу несколько производных карт Л —> (В, С, . , N). Например, по топографической карте строят

248 Глава XIII. Исследования по картам

карты расчленения рельефа, уклонов, экспозиции склонов и др. В других случаях карту А последовательно преобразуют в карту В, ее, в свою очередь, — в карту С и т.д.: А -> В -> С -> . -> N. Допустим, по карте рельефа сперва строят карту глубины расчле­нения, затем последовательно — производные карты интенсивно­сти смыва, эрозионной опасности, почвозащитных мероприятий и т.п. При изучении структуры сложных явлений часто применяют древовидные преобразования, сочетая параллельные и последова­тельные варианты.

Изучение взаимосвязей

Анализ и количественная оценка внутренних и внешних свя­зей и взаимозависимостей между геосистемами, их подсистемами и отдельными компонентами — одна из центральных задач в на­уках о Земле. В ее решении картографическому методу принадле­жит коронная роль благодаря поистине неисчерпаемому разнооб­разию карт всевозможной тематики. По ним удобно оценивать изменчивость связей в пространстве, выделять основные и второ­степенные зависимости, а также выполнять индикационные ис­следования, т.е. предсказывать размещение одних (индицируемых) явлений по другим (индикаторам).

Для изучения взаимосвязей используют широкий арсенал тех­нических приемов. Самые простые среди них — визуальный анализ и описание взаимосвязей. Из графических приемов эффективно совмещение контуров анализируемых явлений на общей основе— графический оверлей, в результате чего выявляют совпадающие, частично совпадающие и совсем не совпадающие контуры. Они трактуются как отражение взаимосвязей различной силы.

Многие зависимости наглядно видны на комплексных профи­лях и разрезах, совмещенных розах-диаграммах (см. рис. 12.6 и12.7), составленных по сериям карт, а также на блок-диаграммах и мета-хронных диаграммах.

Конечно, наилучшие возможности для изучения и количествен­ной оценки взаимосвязей явлений предоставляют аппарат теории корреляции и информационный анализ: коэффициенты корреля­ции, показатели взаимного соответствия и др. (см. разд. 12.7).

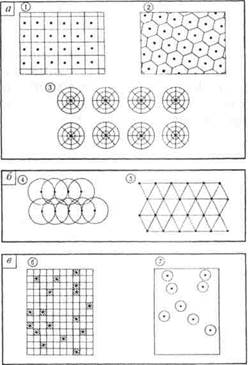
Следует иметь в виду одну важную особенность картографи­ческого метода исследования.

Рис. 13.9. Сходство картографических изображений при отсутствии при­чинной связи между явлениями (Южная Армения). а — плотность сельского населения; б — цветение картофеля.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник