Способ математического программирования это

Математическое программирование

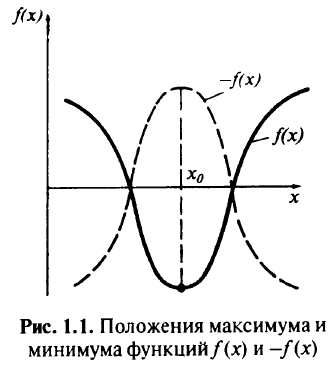
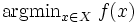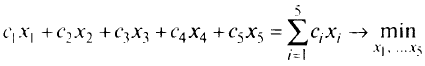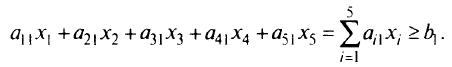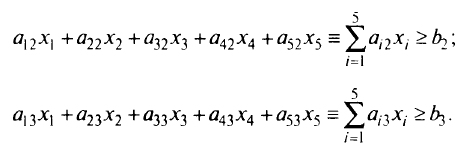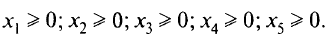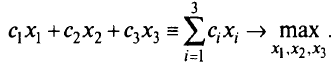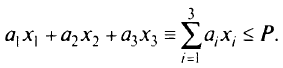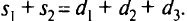Математическое программирование

Математическое программирование — математическая дисциплина, изучающая теорию и методы решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).

Формально, задача математического программирования формулируется так:

Найти

В зависимости от природы множества X задачи математического программирования классифицируются как:

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

• Определение границ системы оптимизации
  • Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
• Выбор управляемых переменных
  • «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
• Определение ограничений на управляемые переменные
  • … (равенства и\или неравенства)
• Выбор числового критерия оптимизации
  • Создаём целевую функцию

История

Задачи линейного программирования были первыми, подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 г. Ж. Фурье и затем в 1947 г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.

Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Дж. Данцигом в 1949 г. для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях. Поэтому наименование «Математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.

Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 30-м годам ХХ столетия. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман, знаменитый математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя; советский академик, лауреат Нобелевской премии (1975 г.) Л. В. Канторович, сформулировавший ряд задач линейного программирования и предложивший (1939 г.) метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.

В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».

Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 г разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л. В. Канторовича, В. С. Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, А. Г. Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем. Методам линейного программирования посвящено много работ зарубежных ученых. В 1941 г. Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 г Дж. Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Г. Куна (англ.), А. Таккера (англ.), Гасса (Gass S. I.), Чарнеса (Charnes A.), Била (Beale E. M.) и др.

Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 г была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.

Начиная с 1955 г опубликовано много работ, посвященных квадратическому программированию (работы Била, Э. Баранкина (Barankin E.) и Дорфмана (Dorfman R.), Франка (Frank M.) и Вольфа (Wolfe P.), Г. Марковица и др.). В работах Денниса (Dennis J. B.), Розена (Rosen J. B.) и Зонтендейка (Zontendijk G.) разработаны градиентные методы решения задач нелинейного программирования.

В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.

Источник

Математическое программирование

Здравствуйте, на этой странице я собрала полный курс лекций по предмету «Математическое программирование».

Лекции подготовлены для школьников и студентов любых специальностей и охватывает полный курс предмета «Математическое программирование», можно даже назвать — это онлайн учебником.

В лекциях вы найдёте основные законы, теоремы, формулы и подробную теорию с примерами решения.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных. wikipedia.org/wiki/Оптимизация_(математика)

Что такое математическое программирование

Математическое программирование — это математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями в виде равенств и неравенств. Название «математическое программирование» связано с тем, что целью решения задач является выбор программы действий.

Деятельность отдельных людей и коллективов, как правило, связана с выбором таких решений, которые позволили бы получить некие оптимальные результаты — затратить минимум средств на питание семьи, достичь максимальную прибыль на предприятии, добиться наилучших показателей в спорте и т.д. Но в каждой конкретной ситуации надо считаться с реальными условиями, накладываемыми на решение данной задачи. При расчете затрат на питание следует приобретаете продукты и в таком количестве, чтобы организм получил необходимые ему жиры, белки, углеводы и т. п.; достигнуть максимальной прибыли предприятия нельзя, не учитывая реальных запасов сырья, его стоимости и целого ряда других факторов; для достижения наилучших показателей в спорте необходимо правильно организовать тренировку спортсменов, оптимально использовать имеющиеся технические средства и площадки, правильно сформировать команду. Но чтобы что-то рассчитать, надо формализовать задачу, т. е. составить математическую модель изучаемого явления, поскольку математические методы можно применять не непосредственно к изучаемой деятельности, а лишь к математическим моделям того или иного круга явлений. Результаты исследований математических моделей представляют практический интерес только тогда, когда модели адекватно отображают реальные ситуации, достаточно совершенны.

Введение в математическое программирование

Приведенные примеры позволяют выделить в наших моделях цель и сформулировать целевую функцию (оптимизационный критерий): минимум затрат, максимум прибыли, наилучшие спортивные достижения — и условия-ограничения: необходимое количество жиров, белков и углеводов; запасы сырья и его стоимость; возможности спортивных площадок и различные варианты состава команд. Задача отыскания минимума некоторой функции 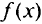эквивалентна задаче отыскания максимума той же функции, взятой со знаком минус (рис. 1.1), и наоборот. Поскольку принципиальных отличий в отыскании минимума и максимума не существует, будем говорить об оптимальном (optimum — наилучший) или

экстремальном значении целевых функций. Итак, сформулированные в реальных задачах требования могут быть выражены количественными критериями и записаны в виде математических выражений, т.е. мы можем перевести условие задачи на математический язык и получить так называемую математическую формулировку задачи. Процесс формирования реальной математической задачи.

Его можно представить в виде следующих этапов:

1. Изучение объекта. Анализ особенностей функционирования объекта; определение факторов, оказывающих влияние (их числа и степени влияния); получение характеристик объекта в различных условиях; выбор оптимизируемого критерия.
2. Описательное моделирование. Установление и словесная фиксация основных связей и зависимостей между характеристиками процесса или явления с точки зрения оптимизируемого критерия.
3. Математическое моделирование. Перевод описательной модели на формальный математический язык. Все условия записывают в виде соответствующей системы равенств и неравенств, а критерий оптимизации — в виде функции. После того как задача записана в математической форме, ее конкретное содержание перестает нас интересовать до проведения содержательного анализа получаемого решения. Дело в том, что различные по своему содержанию задачи часто можно свести к одной и той же формальной математической записи.
4. Выбор или создание метода решения. Исходя из полученной математической записи задачи выбирают либо известный метод решения, либо некую модификацию известного метода, либо разрабатывают новый метод решения. Под допустимым решением понимают такой набор значений искомых величин (переменных), который удовлетворяет поставленным условиям-ограничениям задачи. Решением задачи будет то решение из множества допустимых решений, при котором целевая функция достигает своего наибольшего (наименьшего) значения.
5. Выбор или написание программы для решения задачи на ЭВМ. Задачи, содержащие целевую функцию и условия-ограничения и описывающие поведение реальных объектов, как правило, имеют большое число переменных и большое число зависимостей (уравнений связи) между ними. Поэтому в разумные сроки они могут быть решены только с помощью ЭВМ. Программа для ЭВМ реализует выбранный метод решения задачи.
6. Решение задачи на ЭВМ. Необходимую информацию для решения задачи вводят в память ЭВМ вместе с программой. В соответствии с программой ЭВМ обрабатывает введенную числовую информацию, получает решение и выдает его пользователю в заданной им форме.
7. Анализ полученного решения. Анализ решения бывает формальным и содержательным. При формальном (математическом) анализе проверяют соответствие полученного решения построенной математической модели, т.е. проверяют, правильно ли введены исходные данные, правильности функционируют программа, ЭВМ и т.д. При содержательном анализе проверяют соответствие полученного решения тому реальному объекту, который моделировали. В результате содержательного анализа в модель (словесную и математическую) могут быть внесены изменения, затем весь рассмотренный процесс повторяют.
8. Анализ решения на устойчивость. Аналитически или с помощью численных методов исследуют поведение решения при небольших (в пределах возможных погрешностей или неопределенностей) изменениях исходных данных.

Только после полного завершения анализа модель можно использовать для расчета. Чтобы подчеркнуть важность содержательного анализа, приведем следующий пример. Когда впервые решали задачу о питании, то в качестве фактора оптимизации взяли минимум затрат, а в условие-ограничение включили только требование по калорийности пиши. Решение задачи было таковым: питаться следует уксусом, который входит в состав всевозможных продуктов питания — и калорийность обеспечена, и стоимость минимальна.

Построим математическую модель задачи о питании:

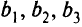
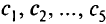
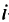
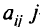
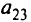
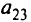
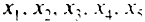
Пусть хозяйка собирается в магазин за продуктами. Предположим, что в рацион семьи входят три различных питательных вещества и требуется их соответственно не менее единиц. В магазине продается пять различных продуктов по цене . Единица продукта -го вида содержит -го питательного вещества, например показывает, что в единице второго продукта третьего питательного вещества будет единиц. Какое количество продуктов каждого вида следует купить хозяйке. чтобы стоимость продуктов была минимальна, но в то же время рацион семьи содержал все необходимые питательные вещества в нужном количестве.

Целевая функция этой задачи — минимизировать по 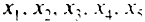стоимость продуктов:

Условия-ограничения задачи: количество первого питательного вещества должно быть не менее 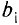т.е.

Аналогично для других питательных веществ получим неравенства

Очевидно, что количество продуктов

Разработкой методов решения задач, содержащих целевую функцию и условия ограничения (задачи на условный экстремум), занимается раздел математики — математическое программирование.

Общие положения математического программирования

Математическое программирование — математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями в виде равенств и неравенств. Название «математическое программирование» связано с тем, что целью решения задач является выбор программы действий.

Отдельные задачи математического программирования и методы их решения известны давно. Так, в числе старинных русских задач по математике есть следующая.

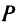
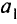
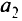
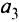
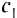
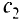
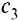
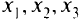
Сколько надо взять бабе на базар для продажи живых гусей, уток и кур, чтобы выручить как можно больше денег, если можно взять товар весом не более кг. При этом известно, что — вес одной курицы, — вес одной утки, — вес одного гуся, — стоимость одной курицы, — стоимость одной утки, — стоимость одного гуся. Пусть — число соответственно кур, уток и гусей, взятых бабой для продажи.

Целевая функция в этой задаче — максимальная стоимость птицы:

Условие-ограничение — вес товара, который может взять баба:

Среди старинных задач по математике встречается задача о ке-нигсбергск их мостах, сформулированная и решенная известным математиком Леонардом Эйлером в 1736 г.: можно ли поочередно обойти все семь мостов города Кенигсберга, соединяющих районы этою города с островом на реке Прегель, пройдя по каждому мосту только один раз. Как мы увидим дальше, это тоже задача математического программирования.

Принципиальные результаты теории оптимизации, явившейся основой математического программирования, были получены еще в период становления математического анализа. В этой связи следует отметить теорему французского математика П. Ферма (1601 — 1665) о необходимом условии локального экстремума в безусловной задаче оптимизации и исследования другого французского математика Ж. Лагранжа (1736-1815) в теории условных экстремумов, указывающие необходимые условия эксгремума в задаче оптимизации при наличии ограничений в виде равенств. Ж. Лагранж предложил метод решения задач на условный экстремум (1797), который заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — функции Лагранжа. Сам метод получил название метода (неопределенных) множителей Лагранжа. Функцию Лагранжа применяют как при исследовании задач вариационного исчисления, так и задач математического программирования.

Естественное развитие методов математического анализа, посвященных определению точек экстремумов функций, привело к таким математическим дисциплинам, как вариационное исчисление и математическое программирование. Вариационное исчисление — математическая дисциплина, занимающаяся отысканием экстремальных (наибольших и наименьших) значений функционалов переменных величин, зависящих от выбора одной или нескольких функции. Одной из первых задач вариационного исчисления была знаменитая задача о брахистохроне И. Бернулли (1696): определить форму кривой, лежащей в вертикальной плоскости, по которой тяжелая материальная точка, двигаясь под действием одной только силы тяжести и не имеющая начальной скорости, перейдет из верхнего положения в нижнее за минимум времени. Эта задача сводится к отысканию функции 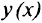, доставляющей минимум функционалу

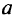
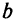
где и — абсциссы верхней и нижней точек.

Несмотря на столь ранние истоки математического программирования, его развитие относится к концу 30-х годов XX столетия. Математическое программирование развивалось как метод решения задач управления и планирования, а также в связи с возникшими в 50-е годы разделом математики «исмедование операций» и совокупностью методологических средств, называемых системным анализом.

Наиболее разработанным разделом математического программирования является линейное программирование, содержащее теорию и методы решения условных экстремальных задач, в которых критерии оптимальности линейно зависят от неизвестных, а ограничения есть линейные равенства и неравенства. Развитие линейного программирования тесно связано с задачами управления и планирования. Первые публикации по линейному программированию принадлежат советскому ученому Л. В. Канторовичу (Математические методы в организации и планировании производства. Ж: Изд-воЛГУ, 1939. С. 67), удостоенному в 1975 г. совместно с американским ученым Т. Купмансом Нобелевской премии за вклад в теорию оптимизации распределения ресурсов.

Математическое программирование стало бурно развиваться наряду с развитием вычислительной техники и применением ЭВМ в научных исследованиях. Появление быстродействующих вычислительных машин создало мощные предпосылки для автоматизации многочисленных задач управления и стимулировало разработку специальных новых математических методов, позволяющих сводить решение задач управления и планирования к последовательности автоматически выполняемых операций в соответствии с исходной информацией, — математического, в основном линейного, программирования.

Методы математического программирования применялись и одновременно развивались во время Второй мировой войны для планирования военных операций. Еще до ее начала методы анализа военных систем с использованием математического программирования стали применяться военными специалистами в Великобритании, а затем и в других странах. В США и Канаде были созданы специальные подразделения, занимавшиеся анализом военных операций. В 1938 г. в США был введен термин «исследование операции» для характеристики рода деятельности необычной исследовательской группы, созданной по инициативе Air Ministry Research Station и выполнявшей работы по анализу военных систем, в частности решавшей задачи оптимального использования радиолокационных установок в обшей системе обороны страны. Этот анализ являлся основой для принятия командованием соответствующих решений. Впоследствии исследование операций сформировалось в научное направление.

Исследование операций — научный метод выработки количественно обоснованных рекомендаций по принятию решений. Описание всякой задачи исследования операций включает задание компонентов (факторов) решения, налагаемых на них ограничений и системы целей. Каждой из целей соответствует целевая функция, заданная на множестве допустимых решений, значения которой выражают меру осуществления цели.

Среди задач исследования операций выделяются те, в которых имеется одна целевая функция, принимающая численные значения. Это и есть задачи математического оптимального программирования, т.е. математическое программирование — раздел науки об исследовании операций. Задачи с несколькими целевыми функциями или с одной целевой функцией, но принимающей векторные значения или значения еще более сложной природы, называют много критериальными. Они решаются либо путем сведения к задачам с единственной целевой функцией либо на основе использования теории игр.

Задачи исследования операций классифицируют и по их теоретико-информационным свойствам. Если субъект в ходе принятия решения сохраняет свое информационное состояние, т.е. никакой информации не приобретает и не утрачивает, то принятие решения можно рассматривать как мгновенный акт. Соответствующие задачи называются статическими. Напротив, если субъект в ходе принятия решения изменяет свое информационное состояние, получая или теряя информацию, то в такой динамической задаче обычно целесообразно принимать решение поэтапно (многошаговые решения). Значительная часть теории динамических задач исследования операций входит в динамическое программирование.

С конца 40-х годов сфера приложения исследования операций стала охватывать разнообразные стороны человеческой деятельности. Исследование операций используется для решения как чисто технических (особенно технологических), так и технико-эко-номических задач, атакже задач управления на различных уровнях.

Лишь отдельные задачи исследования операций поддаются аналитическому решению и сравнительно немногие — численному решению вручную. Поэтому рост возможностей исследования операций тесно связан с прогрессом вычислительной техники.

В настоящее время издается большое число научных журналов по исследованию операций, первый из которых был излан в 1950 г. В 1957 г. в Лондоне был созван первый конгресс Международной Федерации обществ исследования операций (International Federation of Operations Research Societies — 1FORS); эти конгрессы проводят каждые три года.

С 50-х годов XX столетия для обоснований решений по сложным проблемам в системах политического, социального, военного, экономического, научного и технического характера стала применяться совокупность методологических средств, получившая название системный аншиз. Системный анализ используют для решения таких задач, как распределение производств, мощностей между различными видами изделий, определение будущей потребности в новом оборудовании и в рабочей силе той или иной квалификации, прогнозирование спроса на различные виды продукции, а также при решении проблем, связанных с развитием и техническим оснащением вооруженных сил, освоением космоса и т.д.

Системный анализ опирается на ряд прикладных математических дисциплин и разделов, в частности на исследования операций. Когда в задаче системного анализа имеется одна четко выраженная цель, степень достижения которой можно оценить на основе одного критерия, испольуют методы математического программирования. Первое применение системного анализа в военном деле относят к истории древних веков, когда правитель Сиракуз обратился к Архимеду с просьбой помочь осажденному городу прорвать осаду римлян.

Отдельные исследования по системному анализу проводились в конце XIX и начале XX веков, а также в Первую мировую войну. Так, в 1886 г. военное командование прибегло к системному анализу. чтобы принять решение относительно производства 12-дюймовых орудий (1 дюйм — 2,54см), заряжающихся с казенной части и предназначенных для использования в береговой артиллерии. Необходимо было сделать выбор между орудием, выпускаемым фирмой Круппа, и орудием нового образца американского производства. Во время Первой мировой войны с помощью системного анализа разрабатывались, например, стратегические планы борьбы с подводными лодками. Но эти работы не имели практическою выхода и были неизвестны. Поэтому во время Второй мировой войны работы пришлось начинать заново. Системный анализ (и его часть — исследование операций) применяли в основном в области тактики, например, чтобы решить: что использовать в первую очередь в качестве радиолокационных помех — пассивные или активные помехи: как определить наиболее эффективные цели для бомбометания; какие из способов обнаружения подводных лодок являются наилучшими и т.п.

После войны центр тяжести исследований сместился с тактических задач на задачи планирования, гак как возникла необходимость создания новых видов оружия. Затем область применения методов исследования операций расширилась настолько, что охватила и военно-политические доктрины государств.

Примерами задач, решаемых с помощью методов исследования операций и использующих математическое программирование, могут быть следующие:

1. разработка методов управления людьми и техникой, обеспечивающих достаточно высокий уровень эффективности деятельности людей;
2. разработка методов использования имеющихся в распоряжении людей техники, обеспечивающей выполнение поставленной задачи с минимальными затратами или с максимальным эффектом;
3. определение техники, материалов, которые необходимо разработать, создать, приобрести и развернуть в рамках обшей стратегии деятельности людей.

Первые две задачи наиболее полно допускают применение формальных методов, которые являются наиболее продуктивными. Методы, используемые при принятии решений и распределении ресурсов в различных областях науки и техники (экономике, торговле и промышленности — управление запасами, назначение персонала, составление маршрутов и т.п.), практически не отличаются и интенсивно развиваются в последние десятилетия.

Важным классом задач математического программирования являются так называемое сетевые (потоковые)задачи, в терминах которых могут быть сформулированы задачи линейного программирования. Рассмотрим в качестве примера так называемую транспортную задачу, являющуюся одной из первых потоковых задач, решенную в 194I г. ФЛ. Хитчкоком.

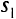
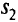
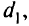
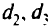
Пусть имеются два завода и три склада. Заводы производят соответственно и единиц продукции, возможности складов — единиц:

Задача состоит в том, чтобы минимизировать затраты на перевозку продукции с заводов на склады.

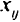
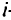
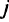
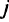
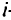
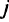
Пусть — объем продукции, который необходимо перевезти с -го завода на -й склад, и — стоимость перевозки единицы продукции с -го завода на -й склад. Тогда целевая функция задачи — стоимость перевозки:

Условия, что вся продукция будет увезена с каждого завода:

Источник