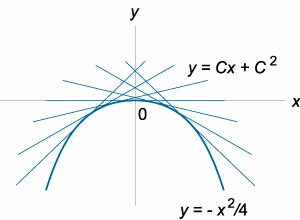
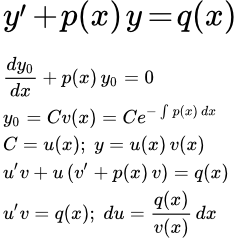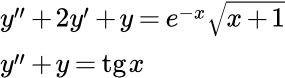Способ лагранжа решения уравнений

Способ лагранжа решения уравнений

Дифференциальное уравнение вида \[y = x\varphi \left( \right) + \psi \left( \right),\] где \(\varphi \left( \right)\) и \(\psi \left( \right)\) − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа .

Полагая \(y’ = p\) и дифференцируя по переменной \(x,\) получаем общее решение уравнения в параметрической форме: \[\left\< \begin x = f\left( \right)\\ y = f\left( \right)\varphi \left( p \right) + \psi \left( p \right) \end \right.\] при условии, что \[\varphi \left( p \right) — p \ne 0,\] где \(p\) − параметр.

Уравнение Лагранжа может также иметь особое решение , если нарушается условие \(\varphi \left( p \right) — p \ne 0.\) Особое решение определяется функцией \[y = \varphi \left( c \right)x + \psi \left( c \right),\] где \(c\) − корень уравнения \(\varphi \left( p \right) — p = 0.\)

Уравнение Клеро имеет вид: \[y = xy’ + \psi \left( \right),\] где \(\psi \left( \right)\) − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда \(\varphi \left( \right) = y’.\) Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением \[y = Cx + \psi \left( C \right),\] в котором \(C\) − произвольная постоянная.

Также как и уравнение Лагранжа, уравнение Клеро может иметь особое решение , которое выражает в параметрической форме: \[\left\< \begin x = — \psi ‘\left( p \right)\\ y = xp + \psi \left( p \right) \end \right.,\] где \(p\) − параметр.

Здесь мы имеем дело с уравнением Лагранжа. Будем решать его методом введения параметра.
Обозначим \(y’ = p,\) так что уравнение можно записать в форме: \[y = 2xp — 3.\] Дифференцируя обе части, получаем: \[dy = 2xdp + 2pdx — 6pdp.\] Дифференциал \(dy\) можно заменить на \(pdx:\) \[ \;\; <\Rightarrow - pdx = 2xdp - 6pdp.>\] Разделив на \(p,\) можно записать следующее уравнение (позже мы проверим, не является ли \(p = 0\) решением исходного уравнения): \[ <- dx = \frac<<2x>>

dp — 6dp,>\;\; <\Rightarrow \frac<><> + \frac<2>

x — 6 = 0.> \] Как видно, мы получили линейное уравнение для функции \(x\left( p \right).\) Интегрирующий множитель будет равен: \[

dp> > \right) > = <\exp \left( <2\ln \left| p \right|>\right) > = <\exp \left( <\ln <<\left| p \right|>^2>> \right) > = <<\left| p \right|^2>> = <.> \] Тогда общее решение линейного дифференциального уравнения имеет вид: \[ \cdot 6dp> + C>><<>> > = <\frac<<\frac<<6>> <3>+ C>><<>> > = <2p + \frac<<>>.> \] Подставляя это выражение для \(x\) в уравнение Лагранжа, находим: \[ <<>>> \right)p — 3 > = <4+ \frac<<2C>>

— 3 > = <+ \frac<<2C>>

.> \] Таким образом, общее решение в параметрической форме определяется системой уравнений: \[\left\< \begin x\left( p \right) = 2p + \frac<<>>\\ y\left( p \right) = + \frac<<2C>>

\end \right..\] Кроме общего решения, уравнение Лагранжа может иметь еще особое решение. Решая алгебраическое уравнение \(\varphi \left( p \right) — p = 0,\) находим корень: \[2p — p = 0,\;\; \Rightarrow p = 0.\] Следовательно, особое решение представляется в виде следующей линейной функции: \[y = \varphi \left( 0 \right)x + \psi \left( 0 \right) = 0 \cdot x + 0 = 0.\]

Здесь мы снова имеем дело с уравнением Лагранжа. Полагая \(y’ = p,\) можно записать: \[2y = 4xp + \ln p.\] Дифференцируем обе части уравнения: \[2dy = 4xdp + 4pdx + \frac<>

.\] Поскольку \(dy = pdx,\) то получаем: \[ <2pdx >>

,>\;\; <\Rightarrow - 2pdx = 4xdp + \frac<>

,>\;\; <\Rightarrow - 2p\frac<><> = 4x + \frac<1>

,>\;\; <\Rightarrow \frac<><> + \frac<2>

x = — \frac<1><<2>>.> \] При делении на \(p\) мы потеряли корень \(p = 0,\) который соответствует решению \(y = 0.\)

Таким образом, мы получаем линейное дифференциальное уравнение для функции \(x\left( p \right).\) Решим его с помощью интегрирующего множителя: \[

dp> > \right) > = <\exp \left( <2\ln \left| p \right|>\right) > = <\exp \left( <\ln <<\left| p \right|>^2>> \right) > = <<\left| p \right|^2>> = <.> \] Функция \(x\left( p \right)\) определяется формулой \[ \cdot \left( < - \frac<1><<2>>> \right)dp> + C>><<>> > = <\frac<< - \frac

<2>+ C>><<>> > = < - \frac<1><<2p>> + \frac<<>>.> \] Подставляя это в исходное уравнение, находим параметрическое выражение для \(y:\) \[ <2y >\;\; <\Rightarrow 2y = 4p\left( < - \frac<1><<2p>> + \frac<<>>> \right) + \ln p,>\;\; <\Rightarrow 2y = - 2 + \frac<<4C>>

+ \ln p,>\;\; <\Rightarrow y = \frac<<2C>>

— 1 + \frac<<\ln p>><2>.> \] Следовательно, общее решение уравнения в параметрической форме записывается в виде: \[\left\< \begin x\left( p \right) = \frac<<>> — \frac<1><<2p>>\\ y\left( p \right) = \frac<<2C>>

— 1 + \frac<<\ln p>> <2>\end \right..\] Чтобы найти особое решение, решим следующее алгебраическое уравнение: \[ <\varphi \left( p \right) - p = 0,>\;\; <\Rightarrow 2p - p = 0,>\;\; <\Rightarrow p = 0.>\] Отсюда следует, что \(y = C.\) Путем прямой подстановки можно убедиться, что постоянная \(C\) должна быть равна нулю.

Итак, заданное дифференциальное уравнение имеет особое решение \(y = 0.\) Мы уже встречались с этим корнем выше при делении уравнения на \(p.\)

Здесь мы имеем дело с уравнением Клеро. Полагая \(y’ = p,\) его можно записать в виде \[y = xp + .\] Продифференцировав по переменной \(x,\) находим: \[dy = xdp + pdx + 2pdp.\] Заменим \(dy\) на \(pdx:\) \[\require <\cancel= xdp + \cancel + 2pdp,>\;\; <\Rightarrow dp\left( \right) = 0.> \] Приравнивая первый множитель к нулю, получаем: \[dp = 0,\;\; \Rightarrow p = C.\] Теперь подставим это во второе уравнение: \[y = Cx + .\] В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых.

Приравнивая нулю второй сомножитель, находим еще одно решение: \[x + 2p = 0,\;\; \Rightarrow x = — 2p.\] Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как \[\left\< \begin x = — 2p\\ y = xp + \end \right..\] Исключая \(p\) из системы, получаем следующее уравнение интегральной кривой: \[

<2>,>\;\; <\Rightarrow y = x\left( < - \frac<2>> \right) + <\left( < - \frac<2>> \right)^2> > = < - \frac<<>> <2>+ \frac<<>> <4>> = < - \frac<<>><4>.> \] С геометрической точки зрения, парабола \(y = — \large\frac<<>><4>\normalsize\) является огибающей семейства прямых, определяемых общим решением (Рисунок \(1\)).

Как видно, это уравнение является уравнением Клеро. Введем параметр \(y’ = p:\) \[y = xp + \sqrt <+ 1> .\] Дифференцируя обе части уравнения по переменной \(x,\) получаем: \[dy = xdp + pdx + \frac<> <<\sqrt <+ 1> >>.\] Поскольку \(dy = pdx,\) то можно записать: \[ <\cancel= xdp + \cancel + \frac<> <<\sqrt <+ 1> >>,>\;\; <\Rightarrow \left( <<\sqrt <+ 1> >>> \right)dp = 0.> \] Рассмотрим случай \(dp = 0.\) Тогда \(p = C.\) Подставляя это в уравнение, находим общее решение: \[y = Cx + \sqrt <+ 1> .\] Графически это решение соответствует однопараметрическому семейству прямых линий.

Второй случай описывается уравнением \(x = — \large\frac

<<\sqrt <+ 1> >>\normalsize.\) Найдем соответствующее параметрическое выражение для \(y:\) \[ + 1> > = < - \frac<> <<\sqrt <+ 1> >> + \sqrt <+ 1> > = <\frac<< - \cancel+ \cancel + 1>> <<\sqrt <+ 1> >> > = <\frac<1> <<\sqrt <+ 1> >>.> \] Параметр \(p\) можно исключить из формул для \(x\) и \(y.\) Возводя последние уравнения в квадрат и складывая их, получаем: \[ <+ > = <<\left( < - \frac

<<\sqrt <+ 1> >>> \right)^2> + <\left( <\frac<1> <<\sqrt <+ 1> >>> \right)^2> > = <\frac<\cancel<+ 1>> <\cancel<+ 1>> = 1.> \] Полученное выражение является уравнением окружности радиусом \(1,\) расположенным в начале координат. Таким образом, особое решение представляется единичной окружностью в плоскости \(xy,\) которая является огибающей для семейства прямых линий (Рисунок \(2\)).

Источник

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Источник

Примеры решений дифференциальных уравнений второго порядка методом Лагранжа

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

Источник