Умножение на круглые числа.
Под круглым числом в широком смысле слова понимают число, которое оканчивается одним или несколькими нулями. Таковы числа 30, 500, 420, 1700 и т. д. На первом этапе целесообразно рассмотреть умножение не на любое круглое число, а лишь на круглые числа, которые состоят не более, чем из девяти единиц того или иного разряда. Таковы числа 30, 40 и т. п. и числа 400, 700 и т. п., которые в методической литературе принято называть круглыми.
Основной прием умножения на кпуглые числа вытекает из сочетательного закона. Этот закон усваивается учениками с большим трудом, чем переместительный и распределительный законы.
Поэтому в существующих методических руководствах этот случай умножения объясняется детям особенно тщательно и с применением наглядности. Удачную разработку данного вопроса мы находим в методическом пособии Г. Б. Поляка «Преподавание арифметики в начальной школе». Приведем это объяснение полностью.
При объяснении умножения на круглые десятки исходим из задачи, например: В коробке 6 мячей. Сколько мячей в 20 коробках? Выяснив, что для решения этой задачи надо 6 x 20, или повторить 20 раз, мы иллюстрируем ее графически примерно так:
Подсчитываем и находим, что в двух коробках каждого ряда 12 мячей, а всего таких рядов 10; чтобы узнать, сколько мячей в 20 коробках, надо 12 умножить на 10, получим 120. Итак,
6 x 20 = 6 x 2 x 10 = 12 x 10 = 120.
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
| 6 | 6 |
При умножении 8 на 30 устанавливает, что 8 надо повторить слагаемым 30 раз, и начинаем записывать слагаемые так:
| 8 | 8 | 8 |
| 8 | 8 | 8 |
| 8 | 8 | 8 |
Числа каждого ряда дают в сумме 24, а таких рядов 10. Умножаем 24 на 10, получаем 240. Итак, 8 x 30 = 8 x 3 x 10 == 24 x 10 = 240.
Аналогично объясняется решение первых примеров на этот случай умножения.
Переходя после решения нескольких примеров с однозначным множимым к решению примеров с двузначным и многозначным множимым, начинают записывать действия столбиком, например:
Однако и после перехода к такой записи полезно, чтобы ученики на первых порах объясняли действие так же, как и при записи в строчку; например, чтобы умножить 38 на 60, надо 38 умножить на 6 и полученное число умножить на 10. Умножаем 38 на 6, получаем 228. Умножаем 228 на 10, получаем 2280.
После решения ряда примеров с таким объяснением ученики формулируют соответствующее правило».
Аналогично умножению на десятки проводится изучение умножения на круглые сотни, круглые тысячи и т. д. Во всех этих случаях множитель подписывают под множимым так, чтобы значащая цифра множителя стояла под единицами множимого, например:
Особого внимания заслуживают те случаи, когда оба сомножителя представляют собой ту или иную комбинацию десятков и круглых сотен, например: 300 x 50; 800 x 300; 400 • 700 и т. д. При решении таких примеров ученики рассуждают следующим образом: чтобы умножить 800 на 300, надо 8 сотен умножить на 3, получится 24 сотни, или 2400; к этому числу остается приписать два нуля, получится 240 000.
Такие примеры, как 800 x 300; 700 x 800; 4000 x 600 и т. д., записывают «в строчку» и решают устно.
Умножение на десятки и круглые сотни следует, сопоставить с умножением любого круглого числа на однозначное. Важно, чтобы ученики уяснили себе значение приписки нулей в том и другом случае: при умножении круглого числа приписка нулей означает раздробление единиц высшего разряда в простые единицы, а при умножении на круглое число приписка нулей означает умножение на соответствующую разрядную единицу.
В устных упражнениях полезно давать в сопоставлении умножение десятков и круглых сотен на число и числа на десятки и круглые сотни (30 x 6 и 13 x 30, 400 x 6 и 14 x 400).
Наряду с приведенными упражнениями следует давать задачи и составные примеры, которые решаются с использованием сочетательного закона умножения. Вот образец такой задачи: Товарный поезд прошел 675 км. Пассажирский поезд был в пути втрое больше и шел вдвое скорее. Сколько километров прошел пассажирский поезд?
Эту задачу можно решить несколькими способами.
Первый способ: 1) 675 км x 2= 1350 км; 2) 1350 км x 3 = 4050 км.
Второй способ: 1) 2 x 3 = 6; 2) 675 км x 6 = 4050 км.
Пример 23 x 2 x 5 можно решить либо приемом последовательного умножения (23 x 2 = 46, 46 x 5 = 230), либо через замену сомножителей 2 и 5 их произведением (2 x 5 = 10; 23 x 10 = 230).
Источник
Эффективный счёт в уме или разминка для мозга
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
Теперь не кажется невозможным умножить в уме 625 на 53:
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
Тогда предыдущий пример можно вычислить немного проще:
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Источник
Разработка урока по математике для начальных классов «Умножение круглых чисел»
Описание разработки
Цель:
Познакомить с приемом умножения круглых чисел.
Задачи:
1) формировать умение умножать круглые числа, пользуясь алгоритмом умножения круглых чисел, совершенствовать навык табличного умножения, решения задач;
2) развивать мыслительные операции, речь, навыки рефлексии;
3) воспитывать интерес к математике.
Планируемые результаты.
знать приём умножения круглых чисел, в том числе и алгоритм умножения круглых чисел;
уметь применять алгоритм умножения круглых чисел;
выбирать необходимый алгоритм в соответствии с типом задачи;
использовать приём умножения круглых чисел при решений конкретных задач;
анализировать текстовые задачи, планировать и реализовывать решение, пояснять ход решения, искать разные способы решения, соотносить полученный результат с условием задачи и оценивать его правдоподобие
мотивация к обучению и целенаправленной познавательной деятельности; формировать самооценку на основе успешности; оценивать учебные действия в соответствии с поставленной задачей
умение извлекать информацию из схем, иллюстраций, текстов;
умение на основе анализа объектов делать выводы;
умение построения осознанного высказывания;
умение ставить и формулировать проблему;
умение самостоятельно ставить познавательные цели;
умение планировать и прогнозировать.
умение слушать и понимать других;
умение строить речевое высказывание в соответствии с поставленными задачами;
умение аргументировать своё мнение и позицию.
умение выполнять пробное действие;
умение фиксировать индивидуальное затруднение в пробном действии;
умение оценивать учебные действия в соответствии с поставленной задачей;
умение осуществлять познавательную и личностную рефлексию.
Ход урока.
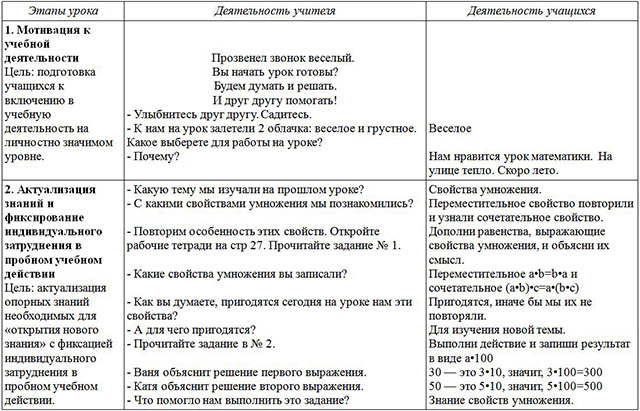
1. Мотивация к учебной деятельности.
Цель: подготовка учащихся к включению в учебную деятельность на личностно значимом уровне.
Прозвенел звонок веселый.
Вы начать урок готовы?
Будем думать и решать.
И друг другу помогать!
— Улыбнитесь друг другу. Садитесь.
— К нам на урок залетели 2 облачка: веселое и грустное. Какое выберете для работы на уроке?
2. Актуализация знаний и фиксирование индивидуального затруднения в пробном учебном действии.
Цель: актуализация опорных знаний необходимых для «открытия нового знания» с фиксацией индивидуального затруднения в пробном учебном действии.
— Какую тему мы изучали на прошлом уроке?
— С какими свойствами умножения мы познакомились?
— Повторим особенность этих свойств. Откройте рабочие тетради на стр 27. Прочитайте задание № 1.
— Какие свойства умножения вы записали?
— Как вы думаете, пригодятся сегодня на уроке нам эти свойства?
— А для чего пригодятся?
— Прочитайте задание в № 2.
— Ваня объяснит решение первого выражения.
— Катя объяснит решение второго выражения.
— Что помогло нам выполнить это задание?
— А кроме этих знаний?
— Как умножить на 10 и 100?
3. Выявление места и причины затруднения, постановка цели деятельности.
Цель: определение места и причины затруднения в пробном учебном действии учащихся, формулировка совместно с учащимися проблемы, цели и задач урока.
Источник
Умножение круглых чисел
Цель: научить выполнять умножение круглых чисел Задачи:
- Рассмотреть приемы умножения круглых чисел на основе переместительного и сочетательного свойств умножения;
- Совершенствовать навык устного счета в пределах 1000, навык решения задач на увеличение в несколько раз, навык решения задач; случаи табличного умножении и деления.
- Развивать мыслительные операции, речь, умение наблюдать, познавательный интерес.
- Воспитывать эстетическую культуру через организацию урока, гуманное и толерантное отношение друг к другу.
Содержимое разработки
Тема: Умножение круглых чисел
Цель: научить выполнять умножение круглых чисел
Задачи:
Рассмотреть приемы умножения круглых чисел на основе переместительного и сочетательного свойств умножения;
Совершенствовать навык устного счета в пределах 1000, навык решения задач на увеличение в несколько раз, навык решения задач; случаи табличного умножении и деления.
Развивать мыслительные операции, речь, умение наблюдать, познавательный интерес.
Воспитывать эстетическую культуру через организацию урока, гуманное и толерантное отношение друг к другу.
Тип урока: комбинированный
Вид урока: открытие нового знания (изучение нового)
Основные дидактические методы: проблемные методы обучения продуктивно — практический
объяснительно-иллюстративный частично – поисковый
принципы самоорганизации познавательной работы учащихся
для учителя – презентация, слайды на интерактивной доске
для учащихся – учебник-тетрадь, карточки для групповой работы и работы в парах.
Самоопределение к деятельности (орг. момент).
Источник