- Выборочное наблюдение в статистике
- Понятие и виды выборочного наблюдения
- Ошибки выборки
- Выборочное наблюдение и Виды совокупности
- Выборочное наблюдение
- Виды совокупности
- Преимущества выборочного метода над сплошным
- Основные этапы проведения выборочного наблюдения
- Виды выборки по методу
- Доля выборки
- Выборочная доля
- ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Выборочное наблюдение в статистике
Понятие и виды выборочного наблюдения
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом число единиц в выборке обозначают n, а во всей ГС — N. Отношение n/N называется относительный размер или доля выборки.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора в выборку:
- Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Ошибки выборки
Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая 

Разности 

Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки по формулам:


где Дв — выборочная дисперсия.
Например, на заводе с численностью работников 1000 чел. проведена 5%-ая случайная бесповторная выборка с целью определения среднего стажа работников. Результаты выборочного наблюдения приведены в первых двух столбцах следующей таблицы:
X, лет
(стаж работы)f, чел.
(число работников в выборке)Xиf
Источник
Выборочное наблюдение и Виды совокупности
Выборочное наблюдение
Выборочное наблюдение есть такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, затем отобранная часть изучается, а далее результаты распространяются на всю исходную совокупность. В задачах по статистике наблюдение происходит таким образом, что эта часть отобранных единиц в уменьшенном масштабе представляет всю совокупность.
Виды совокупности
Генеральная совокупность — это совокупность, из которой производится отбор. Все обобщающие показатели данной совокупности называются генеральными.
Выборочная совокупность — это совокупность отобранных единиц. Все ее обобщающие показатели получили название выборочных.
Преимущества выборочного метода над сплошным
Главные причины, по которым во многих случаях выборочному наблюдению отдают предпочтение перед сплошным:
- Достижение большой точности результатов исследования благодаря сокращению ошибок, происходящих при регистрации.
- При обращении к выборкам обеспечивается экономия материальных, трудовых, финансовых ресурсов и времени в результате сокращения объема работы.
- Сведение к минимуму порчи или уничтожения анализируемых объектов.
- Необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц.
Основные этапы проведения выборочного наблюдения
- Определение нужного объема выборки и способа отбора.
- Проведение отбора.
- Обобщение данных и расчет выборочных характеристик.
- Расчет ошибок выборки.
- Распространение выборочных характеристик на генеральную совокупность.
Виды выборки по методу
Повторная выборка имеет место в схеме возвратного шара. Она характеризуется тем, что численность единиц генеральной совокупности в процессе выборки остается постоянной. Определенную единицу, попавшую в выборку, после регистрации опять возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц снова попасть в выборку. Данный вид выборки очень редко можно встретить в социально-экономической жизни. Вероятность попадания любой единицы в выборку равна 1/N, и она остается постоянной на протяжении всей процедуры отбора.
Бесповторная выборка имеет место в схеме невозвращенного шара. При такой выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращают и в дальнейшем в выборке уже не участвует. При бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования. Вероятность попадания в выборку изменяется от 1/N для первой отбираемой единицы, до1/(N — n -1) для последней.
Доля выборки
Доля выборки рассчитывается как отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности и определяется по формуле:
где N — объем генеральной совокупности (число входящих в нее единиц);
n — объем выборки (число обследованных единиц).Выборочная доля
Выборочная доля (или частность) рассчитывается как отношение числа единиц, которые обладают изучаемым признаком m, к общему числу единиц выборочной совокупности n и определяется по формуле:
Источник
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ



Многоаспектность темы «Выборочное наблюдение» предопределяет рассмотрение выборочных статистических показателей, как с точки зрения получения первичных данных, необходимых для их расчета, так и с точки зрения методов исчисления, оценки репрезентативности, способов распространения на генеральную совокупность.
Выборочным называют наблюдение, основанное на принципе беспристрастного, случайного отбора тех единиц изучаемой совокупности, которые должны быть подвергнуты наблюдению. Выборочное наблюдение – это наиболее совершенный, научно обоснованный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
Преимущества выборочного метода по сравнению со сплошным:
· существенно снижается объем работ по сбору данных и сокращается время на их обработку, что обеспечивает оперативность получения статистической информации в более короткие сроки и с минимальными затратами труда и средств;
· при проведении ряда исследований метод является единственно возможным ( например, при контроле качества продукции проверка сопровождается уничтожением или разложением на составные части обследуемых образцов: сахаристость фруктов, клейковина печеного хлеба, прочность ткани на разрыв, носкость обуви);
· при соблюдении правил научной организации обследования метод дает более точные результаты и применяется для проверки данных сплошного учета( при переписи населения практикуются выборочные контрольные обходы для проверки записей сплошного наблюдения). Минимальная численность обследуемых единиц позволяет провести обследование более тщательно и квалифицированно: в результате снижается вероятность появления ошибок регистрации и необнаружения их на стадии проверки первичной информации;
· по данным выборочного обследования с достаточной точностью определяются возможные расхождения между показателями сплошного и выборочного наблюдения ( возможные пределы отклонений фактических характеристик совокупности от полученных оценок)..
Области применения выборочного наблюдения:
· государственная и ведомственная статистика ( бюджетные обследования семей рабочих и служащих, обследования жилищных условий, суммы доходов и т.п.);
· научно-исследовательские лаборатории и институты;
· демографические обследования ( выборочное обследование доходов и расходов домашних хозяйств);
· социологические обследования и опросы;
· проверка качества готовой продукции, особенно при разрушительных методах контроля;
· в экономике, прежде всего в торговле (качество поступивших товаров, эффективность новых форм торговли, спрос населения на определенные виды товаров, степень его удовлетворения и т.п.);
· определение потерь рабочего времени путем проведения моментных наблюдений или фотографии рабочего дня.
Основные правила формированиявыборочной совокупности:
— каждая единица генеральной совокупности должна иметь равную возможность попадания в выборку ( принцип случайного непредвзятого отбора);
— в выборочную совокупность должны попасть представители всех групп, имеющихся в генеральной совокупности;
— выборочная совокупность должна в основном полно и адекватно воспроизводить закономерности, присущие всей генеральной совокупности ( принцип репрезентативности, представительства).
Систему организации отбора единиц из генеральной совокупности называют способом отбора.В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Способы определения ошибки выборки при различных приемах формирования выборочных совокупностей и распространение характеристик выборки на генеральную совокупность составляют основное содержание статистической методологии выборочного метода.
В зависимости от того, участвуют ли отобранные единицы в дальнейшей выборке или нет, различают 2 метода (схемы) отбора: повторный и бесповторный.

Повторнымназывается такой метод отбора, при котором отобранная однажды единица возвращается обратно в генеральную совокупность и снова участвует в выборке. При повторном отборе сохраняется постоянной вероятность попасть в выборку для всех единиц отбора.
Бесповторнымназывается такой метод отбора, при котором отобранная однажды единица в совокупность единиц, из которых производится отбор, обратно не возвращается. При отборе каждой новой единицы вероятность попасть в выборку изменяется (увеличивается).
Практика применения выборочного метода в экономико- статистических исследованиях использует следующие способы отбора единициз генеральной совокупности:
1) индивидуальный отбор —в выборку отбираются отдельные единицы;
2) групповой отбор— в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор как комбинация индивидуального и группового отбора.
По способу формированиявыборочной совокупности различают следующие виды выборочного наблюдения:
· простая случайная ( собственно случайная)
· типическая (расслоенная или районированная)
Собственно- случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности к численности единиц генеральной совокупности.
При простой случайной выборке отбор единиц производится непосредственно из всей массы единиц в форме случайного отбора, при котором каждой единице генеральной совокупности обеспечивается одинаковая вероятность ( возможность ) быть выбранной. Единица отбора совпадает с единицей наблюдения. Случайный отбор осуществляется путем применения жеребьевки ( лотереи) или путем использования таблиц случайных чисел.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. В соответствии с принятой долей отбора генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой такой группы в выборку отбирается лишь одна единица.
Для обеспечения репрезентативности выборки все единицы генеральной совокупности должны располагаться в определенном порядке и могут быть упорядочены по существенному(в выборку отбирается та единица, которая находится в середине каждой группы), второстепенному или нейтральному признаку
Особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности
Под типической выборкойпонимается такая выборка, когда перед производством ее генеральная совокупность делится на группы по какому-либо типическому признаку ( на типические группы), а затем внутри каждой группы собственно- случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность, а репрезентативность ее обеспечивается расчленением генеральной совокупности на качественно однородные группы. Это обусловливает представительство в выборке каждой типологической группы. Качественно однородные группы при типической выборке могут образоваться в результате специально проведенной группировки единиц генеральной совокупности или же могут использоваться уже имеющиеся, в том числе и естественно сложившиеся явления.
Если общее число единиц выборочной совокупности распределяется между группами пропорционально численности групп в составе генеральной совокупности, то такой отбор называется пропорциональным. Отбор числа единиц из типических групп может быть и непропорциональным численности групп.
Разновидностью типической является районированная выборка, при которой отбор единиц для наблюдения проводится из групп, представленных административно- территориальными образованиями. В этом случае преимущества типической выборки проявляются лишь при заметном расхождении среднего значения изучаемого признака по отдельным регионам.
Сущность серийной (гнездовой) выборки заключается в том, что из генеральной совокупности производится отбор не единиц, а групп (серий, гнезд) собственно- случайным или механическим способом. И далее внутри отобранных серий производится сплошное наблюдение отобранных единиц совокупности, а результаты распространяются на всю совокупность. При серийном (гнездовом) отборе нарушается в какой-то мере равномерность распределения, что влечет за собой более значительную ошибку выборки.
Серийная выборка может проводиться в порядке повторного и бесповторного отбора.Кроме того, серии могут быть равновеликими и неравновеликими.
Выборканазывается многоступенчатой, если отборсовокупности проходит по ступеням , последовательным стадиям. Многоступенчатый отбор предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы ( серии) или отдельные единицы, которые будут подвергнуты наблюдению. То есть единица отбора на каждой ступе ни выборки различна и обследуются только единицы, отобранные на последней ступени.
Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится сначала отбор групп, а затем внутри групп – отбор единиц наблюдения. На обеих ступенях отбор может вестить случайным способом. В отличие от типического отбора, при многоступенчатой выборке производится отбор самих групп, и не все они попадут в выборку.
Многофазная выборка характеризуется тем, что на всех ступенях выборки сохраняется одна и та же единица отбора, но проводится несколько стадий, фаз выборочных обследований, которые различаются между собой широтой программы обследования и объемом выборки. Особенностью многофазной выборки является возможность использовать данные первой фазы наблюдения для дополнительной характеристики и уточнения результатов, полученных на второй фазе, а эти данные в свою очередь на третьей фазе и т.д.
Многофазная выборка может быть связана с многоступенчатой выборкой: на каждой отдельной ступени многоступенчатая выборка может быть многофазной.
Если из одной генеральной совокупности производить одним и тем же способом несколько независимых друг от друга выборок, то такие выборкиназываются взаимопроникающими.Взаимопроникающие выборки применяются в тех случаях, когда необходимо быстро получить предварительные итоги при выборочных обследованиях. Тогда вначале пользуются данными лишь одной выборки, хотя полный размер показателя представляется в виде результатов нескольких выборок.
При проведении взаимопроникающих выборок разными исполнителями можно делать сопоставления итогов по всем частям и обеспечить взаимную проверку их работы. Данные выборки дают независящие друг от друга оценки значений рассматриваемых признаков изучаемой совокупности.
Данный вид выборки удобен для сопоставления результатов исследования по отдельным географическим районам, так как они позволяют выявить межрайонную вариацию, проверить ее расчет по разным выборкам. Ошибки взаимопроникающих выборок определяются по формулам типической пропорциональной выборки.
Подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью и ее численность обозначается буквой N.. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью, или просто выборкой, и ее численность обозначается буквой n.
Обобщающими показателями генеральной совокупности являются:
— средняя (
),
— дисперсия (_
),
— доля (р) – отношение числа единиц, обладающих данным признаком (М), ко всей численности генеральной совокупности (N), то есть
.
Соответственно, обобщающие характеристики в выборочной совокупности, это:
— выборочная средняя (
),
— выборочная дисперсия (_
),
— выборочная доля, частость (w) – отношение числа единиц, обладающих данным признаком в выборочной совокупности(m), к общему объему в ыборочной совокупности (n), то есть
.
Особенностью и преимуществом выборочного метода по сравнению с другими видами несплошного наблюдения является то, что по характеристикам отобранной части единиц можно судить о характеристиках всей совокупности (распространяя результаты выборки на всю совокупность).
В связи с тем, что отобранная для обследования часть совокупности имеет по изучаемому признаку иную структуру, чем совокупность в целом, выборочная совокупность недостаточно точно воспроизводит всю совокупность.. Поэтому при несплошном наблюдении (при выборочном), кроме ошибок регистрации возможны так называемые ошибки представительства.В результате обобщающие характеристики отобранной части(выборочной) более или менее существенно отличаются от обобщающих характеристик всей ( генеральной) совокупности. Соответственно, распространение результатов выборки на генеральную совокупность связано с ошибкой, называемой ошибкой репрезентативности (представительства).
Ошибки репрезентативности могут быть систематическимиили случайными. Систематическиеошибки возникают тогда, когда нарушены принципы отбора (принцип случайности отбора, его тенденциозность). Случайные ошибки возможны и при совершенно правильно организованном отборе за счет того, что случайно могут оказаться отобранными единицы с характеристиками, в среднем отличными от всей совокупности. Случайные ошибки репрезентативности могут быть доведены до незначительных размеров, их величину и пределы можно определить с достаточной точностью на основании закона Больших чисел с использованием, так называемых, предельных теорем теории вероятностей.
Предельные теоремы теории вероятностей выражают основное свойство выборки: если численность выборки достаточно велика, то выборочные характеристики достаточно точно воспроизводят генеральные характеристики. Возможные пределы отклонений выборочной доли и выборочной средней от доли и средней в генеральной совокупности носят название ошибки выборки. Ошибка выборки зависит от ряда факторов:
· степени вариации изучаемого признака,
· методов отбора единиц в выборочную совокупность,
· принятого уровня достоверности результата исследования.
Теорема Чебышева П.Л. применительно к выборочному наблюдению утверждает, что ошибка репрезентативности – разность между выборочной средней и генеральной средней – при достаточно большом числе наблюдений будет сколь угодно малой, то есть
|
–
| — абсолютная величина расхождения между генеральной средней и выборочной средней, представляющая ошибку репрезентативности,
— среднее квадратическое отклонение вариантов выборочной средней от генеральной средней ( средняя ошибка выборки),
t — коэффициент доверия, зависящий от вероятности отклонений выборочной средней от генеральной средней Р(t).
Средняя ошибка выборки (мю) показывает количественную меру возможных отклонений обобщающих характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности.
Величина средней ошибки выборочной средней (
) равна корню квадратному из дисперсии признака, деленной на численность выборочной совокупности, то есть
Размер средней ошибки выборочной доли (
) равен корню квадратному из дисперсии альтернативного признака в выборочной совокупности, деленной на численность выборочной совокупности, или
Приведенные формулы исходят из схемы, так называемой, повторной выборки, суть которой в том, что та или иная единица совокупности, попавшая в выборку, после регистрации снова возвращается в генеральную совокупность, и она при отборе других единиц может снова попасть в выборку.
Часто выборку организуют по схеме бесповторной выборки, при которой единица совокупности, попавшая в выборку, в дальнейшем уже в отборе не участвует, а численность единиц генеральной совокупности в процессе выборки сокращается.
При бесповторной выборке в приведенные выше формулы средней ошибки выборки следует добавить дополнительный множитель в подкоренное выражение, равный разности между единицей и долей отобранных единиц в генеральной совокупности (_
)
Тогда формулы средней ошибки выборки для бесповторного отбора примут вид:
для средней
, для доли
Ошибка выборки при бесповторном отборе всегда будет меньше, чем при повторном отборе.
Приведенные формулы ошибки выборки(μ) характеризуют среднюю величину отклонения сводных характеристик( средней или доли признака) выборочной и генеральной совокупностей.
Однако то, что генеральная средняя (или генеральная доля) не выйдет за определенные пределы, можно утверждать не с абсолютной достоверностью, а лишь с определенной степенью вероятности, на величину которой указывает коэффициент доверия (t).
Следовательно, с определенной степенью вероятности можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки (∆).Предельная ошибка выборки равна произведению средней ошибки выборки (μ) на коэффициент доверия (t), зависящий от вероятности Р(t), с которой можно гарантировать величину предельной ошибки.
Математически это выразится равенством: ∆=μ*t
С увеличением t возрастает вероятность нашего утверждения, но вместе с тем увеличивается и величина ошибки. То есть, чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью можно установить ее величину.
Из теоремы Ляпунова А.М. следует, что вероятность отклонений Р(t). при достаточно большом числе отобранных единиц подчиняется закону нормального распределения и при разных значениях t (связь между t и вероятностью) может быть определена по соответствующей формуле:
Значения интеграла при разных величинах t табулированы и даются в специальных таблицах. Наиболее часто используемые при проведении выборочного обследования вероятности для некоторых t:
при t= 1 P(t) = 0,683, при t= 1,5 Р(t) = 0,866 ,
при t= 2 Р(t) = 0,954, при t= 2,5 Р(t) = 0,988,
при t= 3 Р(t) = 0,997, при t= 3,5 Р(t) = 0,999,
Доверительное число t указывает, что расхождение между характеристиками выборочной и генеральной совокупностей не превысит кратную ему среднюю ошибку выборки «μ».
Например, если t=2, то расхождение между выборочной средней и генеральной средней не превысит 2мю. Или это же выразим иначе: с вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной средними не превысит двукратной величины средней ошибки выборки. То есть, в 954 случаях из 1000 ошибка репрезентативности не выйдет за пределы
.
Аналогично, при t=3 это означает: что с вероятностью 0,997, то есть близкой к достоверности, можно ожидать, что разность между выборочной и генеральной характеристиками не превзойдет трехкратной средней ошибки выборки.
На основе формул предельной ошибки могут быть решены следующие задачи:
1.Определение доверительных пределов генеральной средней (или доли) с заданной вероятностью.
Доверительные интервалы (пределы) будут выражаться следующим образом:
для генеральной средней
-∆
≤
≤
+∆
для генеральной доли
-∆
≤р≤
+∆
2. Определение вероятности того, что расхождение между выборочными и генеральными характеристиками не превзойдет определенную заданную величину (то есть определение доверительной вероятности).
Иногда при расчете выборочных характеристик требуется решить обратную задачу – определить вероятность допуска той или иной ошибки, иначе, отклонения от соответствующих характеристик генеральной совокупности не более, чем на заданную величину, которую можно рассматривать как предельную ошибку выборки ∆=
—
или ∆= р-
Поскольку вероятность является функцией t, то необходимо сначала по исходным данным рассчитать коэффициент кратности (доверия) t по формуле
. А затем по таблице определить соответствующую ему вероятность Р(t ).
3. Определение необходимой численности (объема) выборки, которая с определенной вероятностью обеспечит заданную точность выборочных показателей.
При проектировании выборочного наблюдения необходимая численность выборки определяется исходя из допустимой ошибки при выборочном наблюдении, вероятности, с которой нужно гарантировать величину устанавливаемой ошибки, и способа отбора. Необходимая численность выборки при измерении средней равна среднему квадрату отклонения, деленному на квадрат заданной точности. Формула численности выборки для повторного отбора:
. Если формула содержит в себе коэффициент t, то она приобретает вид:
Необходимая численность выборки при определении доли в случае повторного отбора равна доле, умноженной на дополнение ее до единицы и деленной на квадрат заданной точности. Соответственно, формула имеет вид:
. Или с использованием коэффициента доверия t:
Аналогично для бесповторного отбора формула определения численности выборки при измерении:
средней
, доли
Поскольку при определении численности планируемого выборочного обследования мера колеблемости изучаемого признака (
) и доля альтернативного признака ( р) пока еще не известны, то их величины принимают либо на основании предыдущего опыта ( предыдущих выборок), либо на основании предположений. Также меру колеблемости многовариантного признака(σ) можно найти приближенно по величине предполагаемого размаха вариации (R) формуле: σ= R/ 6, поскольку с вероятностью 0,997 можно утверждать, что размах вариации укладывается при нормальном распределении признака в 6σ.
Аналогично, если доля альтернативного признака неизвестна хотя бы приблизительно, то она принимается равной 0,5 и дает величину дисперсии, равной 0,25.
Рассмотренные выше формулы средней и предельной ошибок выборки приведены применительно к собственно-случайной выборке и ее разновидности – механической выборке. Для типической и серийной выборок эти формулы видоизменяются, конкретизируются в соответствии с особенностями каждого метода.
Так, при типической (районированной) выборке генеральная совокупность делится на группы по определенному признаку, и далее из каждой группы производится случайный отбор единиц. В результате в типическую выборку должны обязательно попасть представители всех групп, что не может иметь места при случайном отборе. Поэтому средняя ошибка типической выборки будет зависеть не от общей дисперсии(
), а от средней из типической выборки групп
.
Соответственно, средняя ошибка пропорциональной типической выборки определяется по формулам:
при повторной выборке
,
при бесповторной выборке
,
Поскольку из правила сложения дисперсий следует, что средняя из внутригрупповых дисперсий

Источник

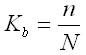





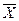 ),
),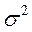 ),
),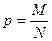 .
.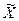 ),
), 
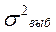 ),
),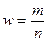 .
.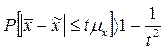
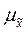 — среднее квадратическое отклонение вариантов выборочной средней от генеральной средней ( средняя ошибка выборки),
— среднее квадратическое отклонение вариантов выборочной средней от генеральной средней ( средняя ошибка выборки),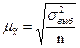
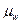 ) равен корню квадратному из дисперсии альтернативного признака в выборочной совокупности, деленной на численность выборочной совокупности, или
) равен корню квадратному из дисперсии альтернативного признака в выборочной совокупности, деленной на численность выборочной совокупности, или 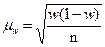
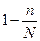 )
)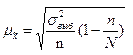 , для доли
, для доли 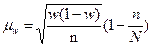
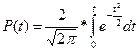
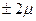 .
.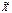 ≤
≤ 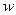 -∆
-∆ 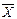 —
— 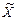 или ∆= р-
или ∆= р- 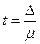 . А затем по таблице определить соответствующую ему вероятность Р(t ).
. А затем по таблице определить соответствующую ему вероятность Р(t ).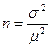 . Если формула содержит в себе коэффициент t, то она приобретает вид:
. Если формула содержит в себе коэффициент t, то она приобретает вид: 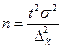
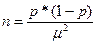 . Или с использованием коэффициента доверия t:
. Или с использованием коэффициента доверия t: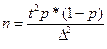
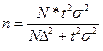 , доли
, доли 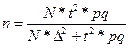
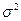 ), а от средней из типической выборки групп
), а от средней из типической выборки групп 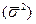 .
.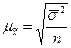 ,
, 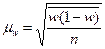
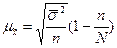 ,
, 


