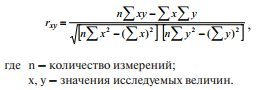Способ корреляционно регрессионного анализа

Применение корреляционно-регрессионного анализа

Больше материалов по теме «Ведение бизнеса» вы можете получить в системе КонсультантПлюс .

В системе статистической обработки данных и аналитики часто используется сочетание методик корреляции и регрессии. Создателем корреляционно-регрессионного анализа считается Фрэнсис Гальтон, который разработал теоретическую основу методологии в 1795 году. В конце 19 века многие европейские ученые в области теории статистики углубили познания в вопросе использования количественных измерителей для отражения связей между явлениями.

Что такое корреляционно-регрессионный анализ (КРА) предприятия?

Корреляционно-регрессионный анализ (КРА) на предприятиях используется для выявления связей между несколькими факторами хозяйственной деятельности и оценки степени взаимозависимости выбранных для анализа критериев. Методика использует два алгоритма действий:

1. Корреляция, которая направлена на построение моделей связей.
2. Регрессия, используемая для прогнозирования событий на основе наиболее подходящей для ситуации модели связей.

Анализ проводится в несколько шагов:

• постановка задач проведения исследования;
• массовый сбор информации: систематизация статистических данных по конкретным показателям деятельности предприятия в динамике за несколько периодов;
• этап создания модели связей;
• анализ функционирования модели, оценка ее эффективности.

Для проведения КРА необходимо использовать показатели в едином измерителе, все они должны иметь числовое значение.

ОБРАТИТЕ ВНИМАНИЕ! Для достоверности данных и работоспособности модели сведения должны быть собраны за длительный отрезок времени.

Для полноты анализа надо устранить количественные ограничения на показатели модели, должно соблюдаться условие постоянной временной и территориальной структуры рассматриваемой совокупности элементов.

Где используется корреляционно-регрессионный анализ?

ВАЖНО! Пример проведения корреляционно-регрессионного анализа от КонсультантПлюс доступен по ссылке

Основные ситуации применения КРА:

1. Тестирование отношения между несколькими величинами: выявляется, что именно этот показатель является влияющим, а второй – зависимым.
2. Определение связи между двумя переменными факторами без уточнения причинно-следственного блока сведений.
3. Расчет показателя по изменению значения другого фактора.

Корреляционно-регрессионная методика анализа может применяться для подготовки данных о разных сторонах деятельности компании. В бизнесе построение моделей зависимости одного показателя от других факторов и дальнейшая эксплуатация выведенной математической формулы позволяют отслеживать оперативное изменение текущей ситуации в выбранном сегменте хозяйствования и быстро принимать управленческие решения.

Например, благодаря КРА можно постоянно отслеживать уровень рыночной стоимости предприятия. Для этого на начальных этапах проводится сбор информации о динамике изменения рыночной стоимости и статистических показателей всех возможных факторов влияния:

• уровень выручки;
• рентабельность;
• размер активов;
• сумма непогашенной дебиторской или кредиторской задолженности;
• резерв сомнительных долгов и др.

Для каждого критерия строится модель, которая выявляет, насколько сильно фактор может влиять на рыночную стоимость бизнес-проекта. Когда все модели построены, оценивается их работоспособность и адекватность. Из комплекса данных выбирается тот тип взаимосвязей, который отвечает требованиям объективности и достоверности. На основе полученной схемы связей создается уравнение, которое позволит получать прогнозные данные об изменении рыночной стоимости при условии изменения значения конкретного фактора.

Методику можно применять при формировании ценовой политики, составлении бизнес-планов, проработке вопроса о расширении ассортиментного ряда и в других сегментах предпринимательства.

Задачи, виды и показатели корреляционно-регрессионного анализа

Задачи КРА заключаются в:

• идентификации наиболее значимых факторов влияния на конкретный показатель деятельности предприятия;
• количественном измерении тесноты выявленных связей между показателями;
• определении неизвестных причин возникновения связей;
• всесторонней оценке факторов, которые признаны наиболее важными для рассматриваемого показателя;
• выведении формулы уравнения регрессии;
• составлении прогноза возможного результата деятельности при изменении ключевых связанных факторов с учетом возможного влияния других факторных признаков.

КРА подразумевает использование нескольких видов корреляционных и регрессионных методов. Зависимости выявляются при помощи корреляций таких типов:

• парная, если связь устанавливается с участием двух признаков;
• частная – взаимосвязь оценивается между искомым показателем и одним из ключевых факторов, при этом условием задается постоянное значение комплекса других факторов (то есть числовое выражение всех остальных факторов в любых ситуациях будет приниматься за определенную неизменную величину);
• множественная – основу исследования составляет влияние на показатель деятельности не одного фактора, а сразу нескольких критериев (двух и более).

СПРАВОЧНО! Выявленные показатели степени тесноты связей отражаются коэффициентом корреляции.

На выбор коэффициента влияет шкала измерения признаков:

1. Шкала номинальная, которая предназначена для приведения описательных характеристик объектов.
2. Шкала ординальная нужна для вычисления степени упорядоченности объектов в привязке к одному и более признакам.
3. Шкала количественная используется для отражения количественных значений показателей.

Регрессионный анализ пользуется методом наименьших квадратов. Регрессия может быть линейной и множественной. Линейный тип предполагает модель из связей между двумя параметрами. Например, при наличии таких двух критериев, как урожайность клубники и полив, понятно, что именно объем поступающей влаги будет влиять на объем выращенной и собранной клубники. Если полив будет чрезмерным, то урожай пропадет. Урожайность же клубники никак не может воздействовать на систему полива.

Множественная регрессия учитывает более двух факторов одновременно. В случае с клубникой при оценке ее урожайности могут использоваться факторы полива, плодородности почвы, температурного режима, отсутствия слизняков, сортовые особенности, своевременность внесения удобрений. Все перечисленные показатели в совокупности оказывают комплексное воздействие на искомое значение – урожайность ягод.

Система показателей анализа формируется критериями классификации. Например, при экстенсивном типе развития бизнеса в качестве показателей могут выступать такие факторы:

• количество сотрудников;
• число заключенных договоров за отчетный период;
• посевные площади;
• прирост поголовья скота;
• расширение дилерской сети;
• объем основных фондов.

При интенсивном типе развития могут применяться следующие показатели:

• производительность труда;
• рентабельность;
• урожайность;
• фондоотдача;
• ликвидность;
• средний объем поставок в отчетном периоде по одному договору.

Оценка

Для оценки достоверности и эффективности модели связей необходимо построить матрицу коэффициентов. Коэффициент в случае парной корреляции вычисляется по формуле:

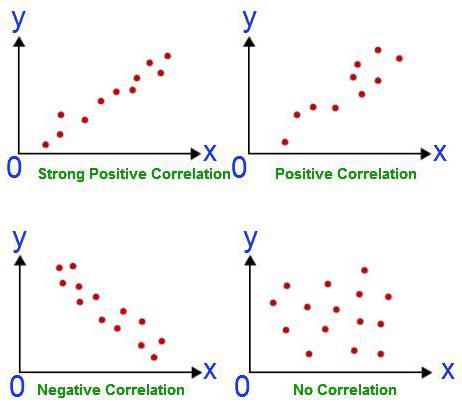
Диапазон значений коэффициента ограничивается показателями от -1 до +1. Если итоговое значение было получено со знаком плюс, то между рассматриваемыми переменными имеется прямая связь. Если в результате расчетов значение оказалось отрицательным, то связь будет обратной, то есть при увеличении одного из показателей другой связанный с ним фактор будет уменьшаться. Пример прямой связи – увеличение посевных площадей будет способствовать росту объема собираемой с полей продукции. Пример обратной связи – увеличение посевных площадей сопровождается снижением урожайности.

Качественный аспект тесноты связи между рассматриваемыми в аналитических расчетах показателями можно оценивать, основываясь на шкале Чеддока.

В соответствии с ее нормами связь будет расцениваться как сильная при значении коэффициента корреляции по абсолютным данным величины выше 0,7. Положительный или отрицательный знак сопровождает числовое значение – неважно, ориентироваться необходимо только на число. Если коэффициент после вычислений оказался ниже 0,3, то связь можно считать слабой.

Для дальнейших этапов анализа выбираются факторы с высокой степенью связанности. Все остальные критерии, для которых установлена слабая связь, отбрасываются. На основании полученных сведений определяется вид математического уравнения регрессии. Рассчитывается численное значение оценки параметров регрессии, определяются качества полученной модели регрессии.

Источник

Корреляционно-регрессионный анализ: пример, задачи, применение. Метод корреляционно-регрессионного анализа

Корреляционно-регрессионный анализ – это один из самых распространенных методов изучения отношений между численными величинами. Его основная цель состоит в нахождении зависимости между двумя параметрами и ее степени с последующим выведением уравнения. Например, у нас есть студенты, которые сдали экзамен по математике и английскому языку. Мы можем использовать корреляцию для того, чтобы определить, влияет ли успешность сдачи одного теста на результаты по другому предмету. Что касается регрессионного анализа, то он помогает предсказать оценки по математике, исходя из баллов, набранных на экзамене по английскому языку, и наоборот.

Что такое корреляционная диаграмма?

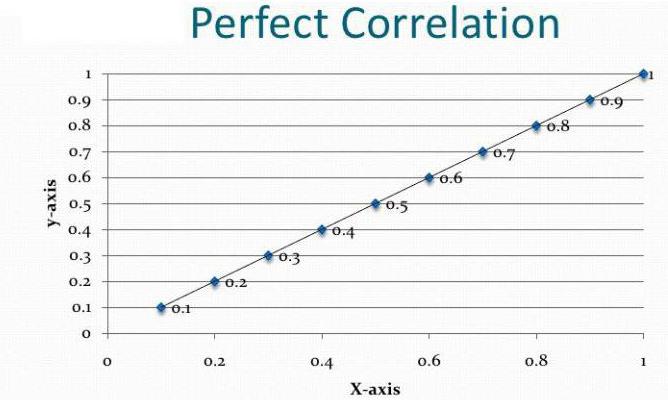
Любой анализ начинается со сбора информации. Чем ее больше, тем точнее полученный в конечном итоге результат. В вышеприведенном примере у нас есть две дисциплины, по которым школьникам нужно сдать экзамен. Показатель успешности на них – это оценка. Корреляционно-регрессионный анализ показывает, влияет ли результат по одному предмету на баллы, набранные на втором экзамене. Для того чтобы ответить на этот вопрос, необходимо проанализировать оценки всех учеников на параллели. Но для начала нужно определиться с зависимой переменной. В данном случае это не так важно. Допустим, экзамен по математике проходил раньше. Баллы по нему – это независимая переменная (откладываются по оси абсцисс). Английский язык стоит в расписании позже. Поэтому оценки по нему – это зависимая переменная (откладываются по оси ординат). Чем больше полученный таким образом график похож на прямую линию, тем сильнее линейная корреляция между двумя избранными величинами. Это означает, что отличники в математике с большой долей вероятности получат пятерки на экзамене по английскому.

Допущения и упрощения

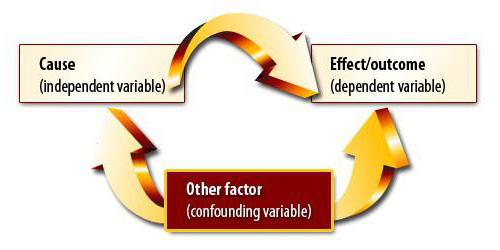
Метод корреляционно-регрессионного анализа предполагает нахождение причинно-следственной связи. Однако на первом этапе нужно понимать, что изменения обеих величин могут быть обусловлены какой-нибудь третьей, пока не учтенной исследователем. Также между переменными могут быть нелинейные отношения, поэтому получение коэффициента, равного нулю, это еще не конец эксперимента.

Линейная корреляция Пирсона

Данный коэффициент может использоваться при соблюдении двух условий. Первое – все значения переменных являются рациональными числами, второе – ожидается, что величины изменяются пропорционально. Данный коэффициент всегда находится в пределах между -1 и 1. Если он больше нуля, то имеет место быть прямо пропорциональная зависимость, меньше – обратно, равен – данные величины никак не влияют одна на другую. Умение вычислить данный показатель – это основы корреляционно-регрессионного анализа. Впервые данный коэффициент был разработан Карлом Пирсоном на основе идеи Френсиса Гальтона.

Свойства и предостережения

Коэффициент корреляции Пирсона является мощным инструментом, но его также нужно использовать с осторожностью. Существуют следующие предостережения в его применении:

1. Коэффициент Пирсона показывает наличие или отсутствие линейной зависимости. Корреляционно-регрессионный анализ на этом не заканчивается, может оказаться, что переменные все-таки связаны между собой.
2. Нужно быть осторожным в интерпретировании значения коэффициента. Можно найти корреляцию между размером ноги и уровнем IQ. Но это не означает, что один показатель определяет другой.
3. Коэффициент Пирсона не говорит ничего о причинно-следственной связи между показателями.

Коэффициент ранговой корреляции Спирмана

Если изменение величины одного показателя приводит к увеличению или уменьшению значения другого, то это означает, что они являются связанными. Корреляционно-регрессионный анализ, пример которого будет приведен ниже, как раз и связан с такими параметрами. Ранговый коэффициент позволяет упростить расчеты.

Корреляционно-регрессионный анализ: пример

Предположим, происходит оценка эффективности деятельности десяти предприятий. У нас есть двое судей, которые выставляют им баллы. Корреляционно-регрессионный анализ предприятия в этом случае не может быть проведен на основе линейного коэффициента Пирсона. Нас не интересует взаимосвязь между оценками судей. Важны ранги предприятий по оценке судей.

Данный тип анализа имеет следующие преимущества:

• Непараметрическая форма отношений между исследуемыми величинами.
• Простота использования, поскольку ранги могут приписываться как в порядке возрастания значений, так и убывания.

Единственное требование данного типа анализа – это необходимость конвертации исходных данных.

Проблемы применения

В основе корреляционно-регрессионного анализа лежат следующие предположения:

• Наблюдения считаются независимыми (пятикратное выпадение «орла» никак не влияет на результат следующего подбрасывания монетки).
• В корреляционном анализе обе переменные рассматриваются как случайные. В регрессионном – только одна (зависимая).
• При проверке гипотезы должно соблюдаться нормальное распределение. Изменение зависимой переменной должно быть одинаковым для каждой величины на оси абсцисс.
• Корреляционная диаграмма – это только первая проверка гипотезы о взаимоотношениях между двумя рядами параметров, а не конечный результат анализа.

Зависимость и причинно-следственная связь

Предположим, мы вычислили коэффициент корреляции объема экспорта и ВВП. Он оказался равным единице по модулю. Провели ли мы корреляционно-регрессионный анализ до конца? Конечно же нет. Полученный результат вовсе не означает, что ВВП можно выразить через экспорт. Мы еще не доказали причинно-следственную связь между показателями. Корреляционно-регрессионный анализ – прогнозирование значений одной переменной на основе другой. Однако нужно понимать, что зачастую на параметр влияет множество факторов. Экспорт обуславливает ВВП, но не только он. Есть и другие факторы. Здесь имеет место быть и корреляция, и причинно-следственная связь, хотя и с поправкой на другие составляющие валового внутреннего продукта.

Гораздо опаснее другая ситуация. В Великобритании был проведен опрос, который показал, что дети, родители которых курили, чаще являются правонарушителями. Такой вывод сделан на основе сильной корреляции между показателя. Однако правилен ли он? Во-первых, зависимость могла быть обратной. Родители могли начать курить из-за стресса от того, что их дети постоянно попадают в переделки и нарушают закон. Во-вторых, оба параметра могут быть обусловлены третьим. Такие семьи принадлежат к низким социальным классам, для которых характерны обе проблемы. Поэтому на основе корреляции нельзя сделать вывод о наличии причинно-следственной связи.

Зачем использовать регрессионный анализ?

Корреляционная зависимость предполагает нахождение отношений между величинами. Причинно-следственная связь в этом случае остается за кадром. Задачи корреляционного и регрессионного анализа совпадают только в плане подтверждения наличия зависимости между значениями двух величин. Однако первоначально исследователь не обращает внимания на возможность причинно-следственной связи. В регрессионном анализе всегда есть две переменные, одна и которых является зависимой. Он проходит в несколько этапов:

1. Выбор правильной модели с помощью метода наименьших квадратов.
2. Выведение уравнения, описывающего влияние изменения независимой переменной на другую.

Например, если мы изучаем влияние возраста на рост человека, то регрессионный анализ может помочь предсказать изменения с течением лет.

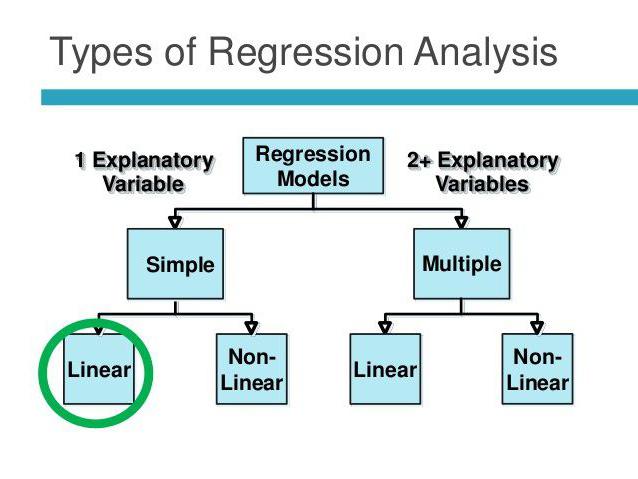
Линейная и множественная регрессия

Предположим, что X и Y – это две связанные переменные. Регрессионный анализ позволяет предсказать величину одной из них на основе значений другой. Например, зрелость и возраст – это зависимые признаки. Зависимость между ними отражается с помощью линейной регрессии. Фактически можно выразить X через Y или наоборот. Но зачастую только одна из линий регрессии оказывается правильной. Успех анализа во многом зависит от правильности определения независимой переменной. Например, у нас есть два показателя: урожайность и объем выпавших осадков. Из житейского опыта становится ясно, что первое зависит от второго, а не наоборот.

Множественная регрессия позволяет рассчитать неизвестную величину на основе значений трех и более переменных. Например, урожайность риса на акр земли зависит от качества зерна, плодородности почвы, удобрений, температуры, количества осадков. Все эти параметры влияют на совокупный результат. Для упрощения модели используются следующие допущения:

• Зависимость между независимой и влияющими на нее характеристиками является линейной.
• Мультиколлинеарность исключена. Это означает, что зависимые переменные не связаны между собой.
• Гомоскедастичность и нормальность рядов чисел.

Применение корреляционно-регрессионного анализа

Существует три основных случая использования данного метода:

1. Тестирование казуальных отношений между величинами. В этом случае исследователь определяет значения переменной и выясняет, влияют ли они на изменение зависимой переменной. Например, можно дать людям разные дозы алкоголя и измерить их артериальное давление. В этом случае исследователь точно знает, что первое является причиной второго, а не наоборот. Корреляционно-регрессионный анализ позволяет обнаружить прямо-пропорциональную линейную зависимость между данными двумя переменными и вывести формулу, ее описывающую. При этом сравниваться могут величины, выраженные в совершенно различных единицах измерения.
2. Нахождение зависимости между двумя переменными без распространения на них причинно-следственной связи. В этом случае нет разницы, какую величину исследователь назовет зависимой. При этом в реальности может оказаться, что на их обе влияет третья переменная, поэтому они и изменяются пропорционально.
3. Расчет значений одной величины на основе другой. Он осуществляется на основе уравнения, в которое подставляются известные числа.

Таким образом корреляционный анализ предполагает нахождение связи (не причинно-следственной) между переменными, а регрессионный – ее объяснение, зачастую с помощью математической функции.

Источник