Определение видимости
Определение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.
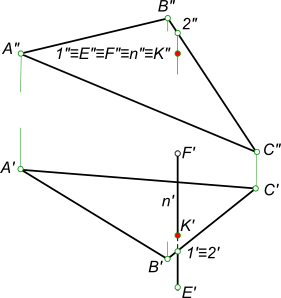
Определение видимости рассмотрим на примерах: — имеется готовый эпюр пересечения прямой с плоскостью заданной треугольником ABC
Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC — это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают. Строим проекции этих точек на плоскости V из условия, что точка 1 принадлежит прямой n, а точка 2 принадлежит стороне треугольника BC. Сравниваем удаление конкурирующих точек 1 и 2 от горизонтальной плоскости проекций — точка 2 является более удаленной. Из проведенного сравнения делаем вывод о видимости заданных геометрических фигур: точка 2 видима и видима плоскость, а точка 1 невидима и ее участок прямой невидим.
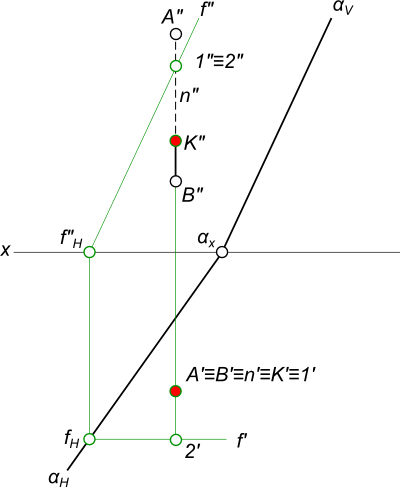
— имеется готовый эпюр пересечения прямой с плоскостью заданной следами
Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α — для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. Это точки 1 и 2 их проекции 1″ и 2″ на плоскость V совпадают. Строим проекции этих точек на плоскости H из условия, что точка 1 принадлежит прямой n, а точка 2 принадлежит фронтали f плоскости α. Сравниваем удаление конкурирующих точек 1 и 2 от фронтальной плоскости проекций — точка 2 является более удаленной. Из проведенного сравнения делаем вывод о видимости заданных геометрических фигур: точка 2 видима и видима плоскость α, а точка 1 невидима и ее участок прямой невидим.
Источник
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
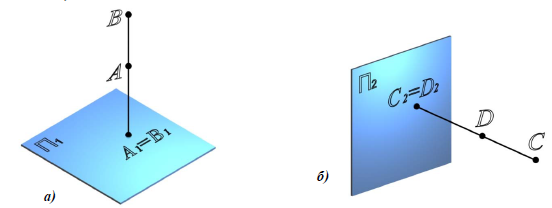
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).
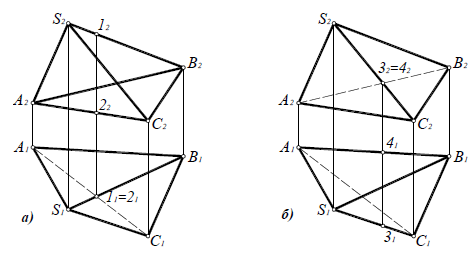
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
Глава 6. Проекции точки. Комплексные чертежи
§ 35. Конкурирующие точки
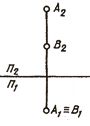
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими . На рис. 64, а приведен комплексный чертеж точек А и В.
Они расположены так, что проекции их совпадают на плоскости П1 [А1≡В1]. Такие точки называются горизонтально конкурирующими .
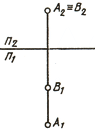
Если проекции точек А и В совпадают на плоскости П2 [А2≡В2] (рис. 64, б), они называются фронтально конкурирующими .
И если проекции точек А и В совпадают на плоскости П3 [А3≡В3] (рис. 64, в), они называются профильно конкурирующими .
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — у которой больше глубина, и у профильно конкурирующих — у которой больше широта.



© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Источник
Способ конкурирующих точек для определения видимости треугольников
Точки, расположенные на одной проецирующей прямой, называются конкурирующими. Точки, расположенные на одной горизотально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 64, а), конкурирующих на горизонтальной плоскости проекций, видима та, высота которой больше (B–видима, A– невидима).
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 64, б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C – видима, D – невидима). Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 65). .
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 65, а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1∈SB и 2∈AC являются конкурирующими на П1, поскольку находятся на проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1 , следовательно, видимо и ребро SB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABC невидима на П1.
Видимость на фронтальной проекции (рис. 65, б) определяется с помощью конкурирующих точек 3∈SC и 4∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SC на фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы наП2 .
Источник
Метод конкурирующих точек



Определение видимости на эпюрах.
Пересечение прямой с плоскостью.
Определение точки встречи прямой с плоскостью относится к элементарным задачам начертательной геометрии, но значение этой задачи большое, так как эта задача входит составной частью в решение многих других позиционных и метрических задач.
Метрические задачи — задачи, в которых определяют размеры геометрических элементов и расстояния между ними.
При пересечении прямой с плоскостью для улучшения наглядности чертежа для показа видимых линий применяют сплошные основные линии, для невидимых линий — штриховые. При показе видимости линий на эпюре предполагается, что:
- Плоскости и поверхности непрозрачные.
- Наблюдатель всегда находится в первой четверти или первой октанте.
- Луч зрения от наблюдателя перпендикулярен к той или иной плоскости проекций (по отношению к которой определяется видимость).
Точки, относящиеся к различным геометрическим объектам и лежащие на одном проецирующем луче, называются конкурирующими в видимости по отношению к той плоскости проекций, к которой проецирующий луч перпендикулярен.
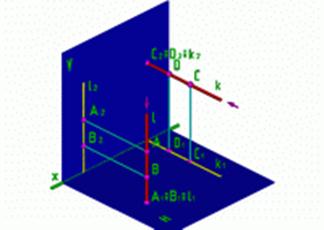 Рис.3 Рис.3 |
Если точка А и точка В лежат на одном проецирующем луче l

Аналогично, С
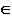

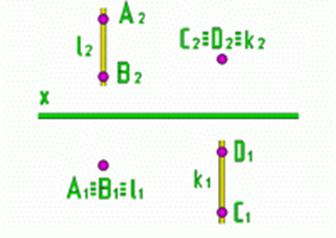 Рис.4 Рис.4 |
На эпюре из двух конкурирующих точек будет видима та проекция, которая дальше отстоит от плоскости проекций, по отношению к которой они конкурируют.
Рассмотрим общий случай: Плоскость и пересекающая ее прямая произвольно расположены в пространстве.
Для нахождения точки встречи прямой с плоскостью в этом случае нужно:
- Через прямую m провести вспомогательную плоскость S; m
S
- Построить прямую пересечения l плоскостей
и S; l=
S.
- Построить точку пересечения К — точку встречи, как результат пересечения прямых l и m. K=l
m.
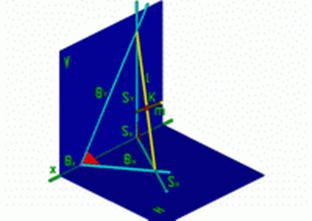 Рис.5 Рис.5 |
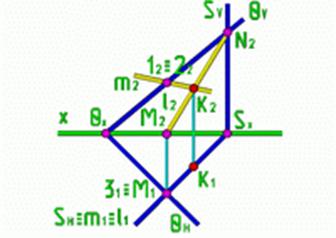 Рис.6 Рис.6 | 12  V 22 V 22 m2 M1 m2 M1  H 31 H 31 m1 m1 |
При определении видимости на плоскость Н рассматриваем проекции конкурирующих точек на плоскость V, а при определении видимости на плоскость V рассматриваем проекции конкурирующих точек на плоскости Н.
Пример. Определить точку встречи прямой m и плоскости Р, заданной треугольником АВС.
Источник

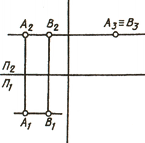





 S.
S.


