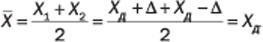Способ компенсации погрешности по знаку

Содержание

КОМПЕНСАЦИЯ СИСТЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ В ПРОЦЕССЕ ИЗМЕРЕНИЯ
Большая Энциклопедия Нефти и Газа
Метод — компенсация — погрешность
Приведите пример компенсации систематической погрешности по знаку.
Методы и способы повышения точности измерений. Части вторая и третья

КОМПЕНСАЦИЯ СИСТЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ В ПРОЦЕССЕ ИЗМЕРЕНИЯ

В практике измерений применяется несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку.

Метод замещения. Этот метод дает наиболее полное решение задачи компенсации постоянной систематической погрешности и представляет собой разновидность метода сравнения. Сравнение производится путем замены измеряемой величины известной величиной и так, чтобы воздействием известной величины привести средство измерения в то состояние, которое оно имело при воздействии измеряемой величины.

Пример. Взвешивание на пружинных весах, у которых имеется постоянная систематическая погрешность (из-за смещения шкалы, например). Взвешивание производится в два приема (см. рис. 1.1, в). Вначале на чашу весов помещают взвешиваемое тело массой m_х и отмечают положение указателя (на отметке N). Затем взвешиваемое тело замещают гирями такой массы m₀, чтобы вновь добиться прежнего отклонения указателя N. Очевидно, что при одинаковости отклонений указателя m_х.= m₀ и систематическая погрешность весов не скажется на результате взвешивания.

Метод противопоставления. Рассмотрим данный метод на следующем примере.

Пример. Взвешивание на рычажных равноплечих весах (см. рис. 1.1, а). Условие равновесия весов m_х l₁ = m₀l₂, отсюда m_х = m₀ (l₂/l₁). Если длины плеч l_1, l₂ одинаковы, то m_х= m_0, Если же l₁ ≠ l₂ (из-за технологического разброса длин плеч при их изготовлении, например), то при взвешивании каждый раз возникает систематическая погрешность

Для исключения этой погрешности взвешивание производится в два этапа. Сначала взвешивают груз m_х, уравновешивая весы гирями массой m₀₁. При этом m_х l₁ = m₀₁ l₂. Затем взвешиваемый груз перемещают на ту чашу весов, где прежде были гири и вновь уравновешивают весы массой m₀₂ гирь. Теперь получим m₀₂ l₂, = m_х l₂. Исключив из равенств отношение l₂/ l₁ найдем

m_х = √ m₀₁ m₀₂

Как видно из формулы, длины плеч не входят в окончательный результат взвешивания.

Метод компенсации погрешности по знаку. Этот метод также предусматривает проведение измерения в два этапа, выполняемых так, чтобы постоянная систематическая погрешность входила в показания средства измерения на каждом этапе с разными знаками. За результат измерения принимают полусумму показаний — систематические погрешности при этом взаимно компенсируются.

Суммирование систематических погрешностей. Независимо от того, к какому виду относится измерение, является ли оно прямым, косвенным, совместным или совокупным, систематическая погрешность результата измерения оценивается, как правило, по ее известным составляющим. Поскольку в каждом конкретном случае каждая систематическая составляющая получает конкретную реализацию (она либо постоянная, либо известен закон ее изменения), то результирующая, суммарная систематическая погрешность представляет собой алгебраическую сумму составляющих:

Источник

Большая Энциклопедия Нефти и Газа

Метод — компенсация — погрешность

Метод компенсации погрешности по знаку применяют для исключения систематических погрешностей, которые в зависимости от условий измерения могут входить в результат измерения с тем или иным знаком, например погрешности от термо — ЭДС, от влияния напряженности постоянного электрического или магнитного поля. В этом случае следует провести измерения дважды так, чтобы погрешность входила в результаты измерений один раз с одним знаком, а другой раз — с обратным. Среднее из результатов двух таких измерений будет свободно от систематической погрешности. [1]

Метод компенсации погрешности по знаку ( метод Двух отсчетов или вилочный метод) используется для устранения систематической погрешности, у которой в зависимости от условий измерения изменяется только знак. Среднее значение из полученных результатов ( х Xi) l2 — хи представляет собой окончательный результат измерения, не содержащий погрешности Ас. Этот метод часто используется при измерении экстремальных значений ( максимума и нуля) неизвестной физической величины. [2]

Метод компенсации погрешностей по знаку предусматривает измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность в результат каждого из них входила с разными знаками. [3]

Подробное рассмотрение методов компенсации погрешностей не входит в задачу настоящей книги. Тем не менее, необходимо отметить, что все они, несмотря на существенные различия в схемах и устройстве, имеют много общего. Достаточно сказать, что одну из главных ролей во всех этих методах играет искусственное улучшение магнитных свойств материала сердечника. Оно достигается за счет использования известной способности ферромагнитных материалов изменять свою магнитную проницаемость в зависимости от величины магнитной индукции. [5]

В некоторых станках используют метод компенсации погрешностей на станках с автоматическим рабочим циклом. Он основан на том, что информацию о погрешностях обработанной детали используют для коррекции траектории инструмента при обработке последующих деталей. Траектория корректируется в ограниченном числе точек. [7]

Значительное распространение при автоматической сборке находит метод компенсации погрешностей замыкающего звена размерной цепи изделия или его части. Сборка изделий с компенсацией вызвана в основном экономическими соображениями, а следовательно, должна базироваться на данных технико-экономического анализа. [9]

Целью настоящей работы является разработка и исследование методов компенсации погрешностей , вызванных нелинейностью и взаимным влиянием измерительных каналов ИП друг на друга, а также апробация их при создании ИИС, не уступающим по метрологическим характеристикам существующим аналогам. [10]

Первая же часть задачи решается обычно с помощью более совершенных, но зато и более сложных методов, — так называемых методов компенсации погрешностей . [11]

В процессе измерения погрешность устраняется применением специальных методов измерения. В практике электроизмерений для устранения постоянной систематической погрешности часто используется метод компенсации погрешности по знаку. Сущность его заключается в следующем: если известна природа погрешности, но не известно ее значение, то нужно измерения производить дважды так, чтобы эта погрешность входила в результаты с противоположными знаками. За действительное значение измеряемой величины принимают полусумму обоих результатов. Метод широко применяется для точных измерений сопротивлений и напряжений мостами и потенциометрами постоянного тока ( см. гл. [12]

Представим себе аналитические ( т.е. применяющиеся для анализа количественного состава веществ) весы, имеющие систематическую погрешность из-за неравенства плеч их коромысла. При измерениях с помощью этих весов постоянную погрешность можно исключить, если произвести статистические измерения в сочетании с использованием метода компенсации погрешности по знаку. Проще говоря, взвешивание нужно произвести несколько раз, меняя местами разновесы и взвешиваемый предмет, каждый из них кладя то на левую, то на правую чашу весов. [13]

Следует предусматривать и использование раздичных приемов для учета, компенсации и устранения погрешностей. В различных областях измерений существуют широко применяемые для исключения известных погрешностей методы, которые могут иметь и собственные названия. Например, метод компенсации погрешности по знаку: процесс измерения строится таким образом, что при выполнении двух наблюдений погрешность в первый результат с одним знаком, а во второй — с другим, и среднее арифметическое полученных результатов не содержит погрешность. Этот метод используют для исключения вариации показаний ( погрешности из-за гистерезиса), выполняя два измерения с противоположными направлениями подачи измеряемой величины. При способе замещения процесс измерения строится так, что измеряемый объект заменяют известной мерой, находящейся в тех же условиях. Так, при точных взвешиваниях на равноплечих весах применяют такой способ: на одну чашку весов устанавливают взвешиваемый предмет, а на другую помещают какой-нибудь груз ( дробь) до уравновешивания. Затем взвешиваемый предмет снимают, и на его место кладут гири. Значение массы гирь, использованных для восстановления равновесия, соответствуют значению массы взвешиваемого предмета. Этот способ точного взвешивания носит специфическое название — способ БорДа. [14]

Источник

Приведите пример компенсации систематической погрешности по знаку.

Метод компенсации погрешности по знаку используют для устранения постоянной систематической погрешности, у которой в зависимости от условий измерения изменяется только знак. При этом методе выполняют два измерения, результаты которых соответственно есть х1 = хu + Δс и х2 = хи — Δс, где хu— измеряемая величина Среднее значение из полученных результатов

(х1 + х2)/2 = хu представляет собой окончательный результат измерения, не содержащий погрешности ± Δс. Данный метод наиболее часто применяют при измерении экстремальных значений (максимума и нуля) неизвестной физической величины.

Пример. Показания вольтметра подвержены влиянию магнитного поля Земли. В результате возникает погрешность измерения ΔU.

Решение. Произведя два измерения напряжения при противоположной ориентации прибора относительно меридиана, получим U1 = Ux + ΔU и U2 = UX- ΔU.Отсюда напряжение Ux= (U1 + U2)/2.

196. Что означает запись p(A)=P?

197. Что такое интервальный систематический ряд?

198. Что такое гистограмма?

Гистограмма – ступенчатая диаграмма, показывающая как часто при измерениях появляются результаты, попадающие в тот или иной интервал Dx между наименьшим x_min и наибольшим x_max из измеренных значений величины x. Гистограмму строят в следующих координатах: по оси абсцисс откладывают измеряемую величину x, по оси ординат – Dn/nDx (рис.3.1). Здесь n – полное количество проведенных измерений, Dn – количество результатов, попавших в интервал [x, x+Dx] .

199. Что такое кривая распределения плотности вероятностей случайной величины?

200. Что собой представляют ординаты кривой распределения случайной величины?

201. Какие стандартные законы распределения случайных величин Вы знаете?

Дата добавления: 2015-01-29 ; просмотров: 11 ; Нарушение авторских прав

Источник

Методы и способы повышения точности измерений. Части вторая и третья

Метод сравнения с мерой основан на том, что размер измеряемой физической величины сравнивают с помощью компаратора с размером физической величины, воспроизводимой мерой, а искомое экспериментальное значение физической величины рассчитывают по полученным значениям показаний компаратора и номинальному значению меры. Применение этого метода является одним из наиболее эффективных способов уменьшения составляющей погрешности измерений, вызванной систематической погрешностью СИ. Рассмотрим разновидности метода сравнения.

Метод замещения — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.

Пример. При измерении электрического сопротивления на мосте постоянного тока этот мост уравновешивают при включенном измеряемом сопротивлении rx, после чего вместо rx включают переменную эталонную меру. Изменяя значение меры, добиваются равновесия моста и по значению эталонной меры определяют измеряемое сопротивление rx. Благодаря такому измерению удается исключить влияние неполной уравновешенности моста, термоконтактных э.д.с. и других причин, вызывающих систематические погрешности.

Метод противопоставления заключается в том, что об отличии сравниваемых размеров физических величин (массы, электрического сопротивления, электрической емкости, индуктивности и др.) судят по показанию специального двухканального компаратора, на оба входа которого сравниваемые физические величины действуют одновременно. Обусловленная несимметрией компаратора составляющая погрешности измерений часто является доминирующей. Она может быть уменьшена методом противоположного влияния.

Пример. Измерение массы на равноплечих весах (см. рисунок 3)

Условеие равновесия весов

Если длины плеч одинаковы l₁ = l₂ , то m_x = m₀ . Если же l₁ ≠ l₂ (например, из-за технологического разброса длин плеч при их изготовлении), то при взвешивании каждый раз возникает систематическая погрешность

Для исключения этой погрешности взвешивание производится в два этапа. Сначала взвешивают груз m_x, уравновешивая весы гирями массой m ₀₁ . При этом .

Затем взвешиваемый груз перемещают на ту чашу весов, где прежде были гири, и вновь уравновешивают весы массой m ₀₂ гирь.

Теперь получим . Исключив из равенства онтношение l₁ / l₂ найдем :

где m_x — искомое значение массы груза,

m ₀₁ , m ₀₂ — значения масс гирь, соответствующие равновесию весов при первом и втором наблюдениях.

Обычно, благодаря тому, что

можно пользоваться более простой формулой:

Как видно из формулы, длины плеч не входят в окончательный результат взвешивания.

Метод компенсации погрешности по знаку заключается в следующем. Процесс измерения строится таким образом, что при выполнении двух наблюдений погрешность входит в первый результат с одним знаком, а во второй — с другим. При этом среднее арифметическое полученных результатов характеризуется минимальной погрешностью.

Пример. Для исключения погрешности измерения, обусловленной влиянием земного магнитного поля на показания прибора, проводят два измерения. Первое — с результатом X₁ и второе — с результатом X₂, полученным при повороте прибора на 180°. Если в эксперименте магнитное поле Земли увеличивало результат на Δ, т.е. X₁ = X_Д + Δ, где X_Д — действительное значение измеряемой величины, то после поворота прибора на 180° результат измеренияX₂ = X_Д — Δ . Среднее значение результатов

Метод рандомизации (от английского random — случайный, беспорядочный; в переводе на русский означает: перемешивание, создание беспорядка, хаоса) — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей, который основан на принципе перевода систематических погрешностей в случайные. При этом выполняют ряд наблюдений, изменяя условия или процедуру измерений таким образом, что фактор, вызывающий данную известную погрешность, изменяется случайным образом. Например, одна и та же величина измеряется различными методами или приборами. Систематические погрешности каждого из них для всей совокупности носят случайный характер. При увеличении числа используемых методов или приборов известные систематические погрешности взаимно компенсируются

Пример. Пусть некоторая физическая величина измеряется n раз (число n достаточно велико) однотипными приборами, имеющими систематические погрешности одинакового происхождения. Для одного прибора эта погрешность — величина постоянная, но от прибора к прибору она изменяется случайным образом. Поэтому если измерить неизвестную физическую величину n приборами и затем вычислить математическое ожидание (среднее арифметическое значение) всех результатов, то значение погрешности существенно уменьшится (как и в случае усреднения случайной погрешности).

В следующий раз мы продолжим разговор о методах и способах повышения точности измерений, с помощью которых можно исключить систематические погрешности в процессе измерений.

Источник

Читайте также:

C2 Покажите на трех примерах наличие многопартийной политической системы в современной России.
C2 Раскройте на трех примерах научный вывод о том, что социальные условия влияют на характер и форму удовлетворения первичных (биологических, витальных) потребностей.
II. Примеры проективных методик
III. Примеры решения задач.
III. Примеры решения задач.
III. Примеры решения задач.
IV. Примеры решения задач.
IV. Примеры решения задач.
IV. Примеры решения задач.
IV. Примеры решения задач.