Схемы включения и компенсации термопар
Как известно, термопара содержит два спая, поэтому для правильного и точного измерения температуры на одном (первом) из спаев, необходимо поддерживать другой (второй) спай при известной постоянной температуре, чтобы измеренная ЭДС оказывалась явной функцией температуры только первого спая — главного рабочего спая.
Так, с целью поддержания в термоизмерительном контуре условий, при которых паразитное влияние ЭДС второго («холодного спая») было бы исключено, необходимо как-то компенсировать в любой рабочий момент времени напряжение на нем. Как это сделать? Как привести схему к такому состоянию, чтобы измеряемое напряжение термопары менялось бы только в зависимости от изменений температуры первого спая, независимо от текущей температуры второго?
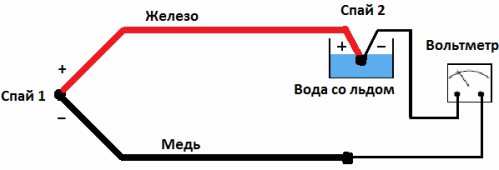
С целью достижения правильных условий, можно прибегнуть к незамысловатой хитрости: поместить второй спай (места присоединения проводов первого спая с измерительным прибором) в емкость с ледяной водой — в заполненную водой ванночку, в которой еще плавает лед. Таким образом получим на втором спае фактически постоянную температуру таяния льда.
После чего останется, отслеживая результирующее напряжение на термопаре, вычислять температуру первого (рабочего) спая, ибо второй спай будет находится в неизменном состоянии, напряжение на нем будет константой. Цель в итоге будет достигнута, влияние «холодного спая» окажется скомпенсировано. Но если так делать, то получится громоздко и не удобно.
Чаще термопары применяются все же в мобильных портативных устройствах, в переносных лабораторных приборах, поэтому нежен другой вариант, ванночка с ледяной водой разумеется нам не подходит.
И такой иной способ есть — метод компенсации напряжения от изменяющейся температуры «холодного спая»: присоединить последовательно к измерительному контуру источник дополнительного напряжения, ЭДС которого будет иметь противоположное направление и по величине будет всегда точно равна ЭДС «холодного спая».
В случае, если ЭДС «холодного спая» непрерывно отслеживается путем измерения его температуры иным способом нежели термопара, — тогда равную компенсирующую ЭДС можно непрерывно тут же прикладывать, сводя суммарное напряжение паразитного участка цепи к нулю.
Но чем же можно непрерывно измерять температуру «холодного спая», чтобы получать непрерывные значения напряжений для автоматической компенсации?
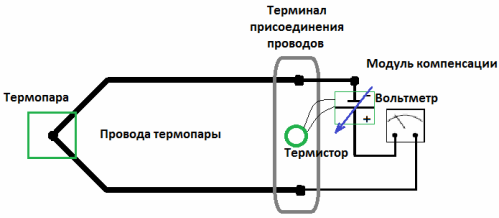
Для этого подойдет термистор или термометр сопротивления, соединенный с типовой электроникой, которая и будет автоматически формировать компенсирующее напряжение необходимой величины. И хотя «холодный спай» не обязательно может быть буквально холодным, его температура, как правило, не такая уж экстремальная, какая может быть у рабочего спая, поэтому обычно подходит даже термистор.
Доступны специальные электронные компенсирующие модули «температуры таяния льда» для термопар, задача которых в том и состоит, чтобы подавать точное противоположное напряжение в измерительную цепь.
Значение компенсирующего напряжения от такого модуля поддерживается на таком значении, чтобы точно компенсировать температуру точек присоединения проводников термопары к модулю.
Температура точек присоединения (на терминале) измеряется термистором или термометром сопротивления, и точно необходимое напряжение автоматически прикладывается последовательно в цепь.
Неискушенному читателю может показаться, что слишком много нагромождений ради просто точного использования термопары. Может быть целесообразнее, да и проще, сразу пользоваться термометром сопротивления или тем же термистором? Нет, не проще и не целесообразнее.
Термисторы и термометры сопротивления не так механически прочны как термопары, да и безопасный рабочий температурный диапазон у них не велик. Дело в том, что термопары обладают рядом преимуществ, два из которых основные: очень широкий температурный диапазон (от −250 °C до +2500 °C) и высокое быстродействие, которое недостижимо на сегодняшний день ни термисторами, ни термометрами сопротивления, ни датчиками иных типов аналогичной ценовой категории.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Программная компенсация температуры «холодного спая» при работе с термопарой
Эта статья родилась, как часть статьи про датчик для работы с термопарой ads1118.
Дело в том, что для повышения точности, компенсировать «холодный спай» необходимо. Первоначально, я имея ряд отсчетов, подобрал некую магическую формулу, которая давала неплохие результаты. Но обоснования ей не было. НО потом, возникла идея, как сделать правильно. А в процессе реализации, стало ясно, что это может быть достаточно простым и универсальным решением для любой ситуации.
Под катом много математики и нет картинок и одна картинка ).
И чтобы далеко не ходить, обещанная картинка с температурой в доме:
Для тех, кому надо результат:
Берем приложенный файл. Делаем 3 замера:
Нагреваем плату с «холодным спаем» и измеряем температуру 100 градусов (кипящую воду).
Остужаем плату (например в холодильнике), и снова измеряем темепературу 100 градусов и 0 градусов.
Заносим данные в верхний левый угол таблицы.
Подбираем коэффициент КТ (первая срока), так, чтобы ошибка была минимальной.
Полученные 4 числа: КТ, С, К1 и К2 используем для перевода «попугаев» в температуру.
Если хочется оптимизаций, то она описана в конце статьи.
Все. Дальше, только математика 🙂
Постановка задачи:
Мы измеряем температуру с помощью термопары, и неким образом знаем температуру «холодного спая» (например припаяв рядом специальную микросхему и читая ее данные).
Задача: нужно минимизировать ошибку измерения имея на входе некое волшебное число А — величина с термопары («горячий спай») и некое волшебное число B — величина температуры «холодного спая», а так-же найти коэффициент самой термопары.
Предварительные мысли:
Как правильно обратил внимание уважаемый DeepSOIC в комментарии к первоначальной статье:
Напряжение на термопаре пропорционально разности температур между её спаем и её разъёмом. Разъём называют «холодный спай» — cold junction — который кстати вовсе не обязательно холодный, просто так называется. Т.е. термопара измеряет не температуру, а разность температур. Чтобы получить полную температуру, нужно измеренную разность температур приплюсовать к температуре холодного спая.
термопара измеряет не температуру, а разность температур
я уяснил только прочитав этот комментарий. Спасибо огромное.
Т.е. нам по сути, необходимо просто прибавить температуру к той, что дает термопара. Проблема в том, что, разница не постоянна, и зависит и от температуры обоих спаев. Приходиться долго экспериментировать, изучать закон изменения разницы. + еще нужно найти коэффициент самой термопары (КТ)… И тут,
Эврика:
А зачем нам все это делать? Если мы допустим, что закон линеен (не линейный закон, мы все равно не вычислим, да и точность нам нужна не до тысячных), то получается элементарная задача:
Дано: 2 числа А и В. Необходимо:
1) Найти КТ
2) Вычислить некое число, линейно зависящее от А, В и КТ.
Из математики, мы получаем единственный вариант:
ЧИСЛО (Ч) = ВОЛШЕБНАЯ КОНСТАНТА (С) + ВОЛШЕБНЫЙ КОЭФФИЦИЕНТ 1 (К1) * А + ВОЛШЕБНЫЙ КОЭФФИЦИЕНТ 2 (К2) * В
Все что нам необходимо, это найти 3 волшебных числа. Т.е. решить систему линейных уравнений с 3-мы неизвестными. Для этого нужно иметь 3 уравнения. Не вопрос: проводим 3 замера (и еще 3 для контроля), подставляем, решаем. Важное дополнение по итогам обсуждения:
необходимо 3-е измерение брать при значительном изменении температуры «холодного спая». Это даст более точное решение.
Например так:
Нагреваем плату с «холодным спаем» и измеряем температуру 100 градусов (кипящую воду).
Остужаем плату (например в холодильнике), и снова измеряем темепературу 100 градусов и 0 градусов.
Остается найти КТ, как число, которое дает минимальную ошибку для тестовых замеров. ВСЕ. Самое интересное, что система не явно, дает самый точный результат, при правильно КТ. Т.е. мы можем просто менять в условиях задачи КТ и смотреть, где ошибка меньше, там точнее КТ.
Математика за нас, учла и смещение 0, и взаимное влияние коэффициентов друг на друга и КТ. Для каждой схемы, решение будет разное. Но решение не зависит от внешних факторов. Оно зависит только от реализации схемы, и учитывает все погрешности и не точности (например разброс номиналов резисторов) — они получаются учтены в результатах тестовых измерений, и в решении они тоже учитываются. Кроме того, системе не важно в каких «попугаях» заданы числа А и В. Единственное требование: (достаточно точная для задачи) линейность этих «попугаев».
Пример из моей задачи:
Должен заметить, что коэффициент КТ, подобран по минимальной ошибке.
Например, при КТ = 6 получается так:
Для упрощения расчетов, я приложил файлик с готовыми формулами. Надо только подставить данные и подобрать КТ.
ВНИМАНИЕ: никаких макросов я не использовал. Если они есть, значит это вирус. Будьте внимательны.
Оптимизация:
Если посмотреть на алгоритм, то расчеты это куча умножений и делений дробных чисел. Это и на ПК не быстро, а уж в МК и подавно… Поэтому я использую хитрость: работу с фиксированной запятой. В итоге, работа только с целыми числами.
Суть: все 3 коэффициента: С, К1 и К2 я умножаю на 65536 (думаю понятно почему 65536 :)):
В результате, число Ч автоматически увеличивается в 65536 раз. Только все операции целочисленные. При вычислении смещения, мы предварительно умножаем значение холодного спая на 65536 и при ЦЕЛОЧИСЛЕННОМ делении 65536 исчезает… 🙂 Конечно, точность немного страдает… Но скорость вырастает на порядки…
Но и тут еще можно поднять точность, используя целые числа, т.к. смещение число не большое, и 1-ка очень важна (1% точности). Мы умножаем значение холодного спая не на 65536, а на 131072. И после деления, прибавляем единичку и делим на 2, чтобы компенсировать ошибку. В итоге получаем округление до 0.5 )
В приложенном файле, есть оба варианта (дробное и целое).
Целое дает ТОЧНЫЙ(. ) результат на тестовых данных. Ошибка 0.
ОБНОВЛЕНИЕ:
По сути мы хотим получить две прямые (но нас интересует их сумма).
Первая прямая — горячий спай,
t1 = k1 * A + c1
Вторая — холодный
t2 = k2 * B + c2
Нас интересует их сумма
t = k1 * A + k2 * B + c (где с = с1 + с2)
К сожалению, мы НЕ ищем прямое преобразование А-В в температуру и НЕ решаем описанные уравнения. Это было бы идеально. И для расчетов (2 умножения, 2 сложения) очень просто и не напряжно для МК. Проблема в том, что это НЕ работает 🙁
По факту, как правильно заметили:
Вообще самое правильное это сначала измеренную температуру холодного спая преобразовать в эквивалентное термо ЭДС (Как если бы холодный спай был при нуле, а рабочий при измеренной температуре), затем сложить это напряжение с измеренным с термопары, а потом уже обратно преобразовать эту сумму в температуру. Таким образом полностью компенсируются нелинейности.
Не понятно откуда взялись числа 28,7414 28,5902 30,9189
Это как раз и есть КОЭФФИЦИЕНТы КОМПЕНСАЦИИ «холодного спая» для заданных условий. Они разные для разных данных.
При дальнейших расчетах, мы делим на этот коэффициент, тем самым внося нелинейность в формулу перевода «попугаев» в температуру.
Пояснение 2, математическое:
Пусть:
t – измеряемая температура
vx – измеренное значение «холодного спая»
vg — измеренное значение «горячего спая»
vg0 — измеренное значение «горячего спая» если бы измерение проводилось при vx = 0
КТ – коэффициент перевода vg0 в t:
Но как правило, vx не равно 0, поэтому нам надо привести vx к нулю, изменив vg на некую величину, зависящую от vx:
Пусть kx – коэффициент компенсации:
Предположим, что kx линейно зависит от vx и vg:
Для нахождения c, k1 и k2, необходимо решить систему линейных уравнений с 3-мя неизвестными для известных kx, vx, vg. vx и vg мы измеряем непосредственно.
kx мы находим по формуле (1) и (2), зная температуру в точках измерения:
Но (5) это уже не линейное уравнение, поэтому проще всего подобрать КТ по минимальной ошибке решая систему линейных уравнений для каждого КТ.
Комментарии ( 22 )
Плохо, что вы проводите калибровку при одинаковом значении температуры холодного спая (вернее его температура, насколько я понимаю, пляшет в пределах погрешности датчика).
По сути мы хотим получить две прямые (но нас интересует их сумма).
Первая прямая — горячий спай,
t1 = k1 * A + c1
Вторая — холодный
t2 = k2 * B + c2
Нас интересует их сумма
t = k1 * A + k2 * B + c (где с = с1 + с2)
Математически верно, но в А и В есть погрешность измерения. Чтобы максимально точно (в данном случае) построить каждую прямую по двум точкам, нужно чтобы эти точки были максимально удалены друг от друга. Чем дальше — тем лучше, тем меньше будет сказываться погрешность.
Для горячего спая (А) у вас разница в 100 градусов, что ИМХО, достаточно для Вашего случая. А вот для холодного — у Вас разница на уровне шума датчика, и вычисленные значения к2 и с2 будут очень грубыми.
Описание получилось путанным, но я думаю суть понятна. Я бы предложил отдельно «линеаризировать» холодный спай на значительной разнице температур (охлаждая и нагревая все устройство).
Хм, просмотрел еще раз внимательно Ваш пост и запутался окончательно. Плюс, в ОпенОфисе приатаченный файл открывается с битой кодировкой.
Давайте начнем с стемы уравнений. Я сразу решил, что в правой части уравнений у вас температура, но там непонятные для меня величины (28,7414 и т д).
Далее, на основании 3-х измерений решили систему уравнений. Получили формулу зависимости.
Теперь в эту формулу мы подставляем результаты 5-го измерения. И что мы получаем? По логике, результат вычисления это апроксимированное значение этой самой «непонятной для меня величины» для 5-го измерения. Только зачем находить ее аппроксимированное значение, ели мы, на сколько я понимаю, можем измерить ее прямыми методами (как для предыдущих случаев). Дальше я совсем потерялся в смысле вычислений.
Если не тяжело, объясните смысл Вашего метода более подробно, с описанием физического смысла получаемых величин (потому как понятие «волшебное число» не способствует пониманию)
мы делим на этот коэффициент, тем самым внося нелинейность в формулу перевода «попугаев» в температуру.
1) Мы должны компенсировать «холодный спай», фактически просто прибавив термоэдс «холодного спая» к «горячему спаю», чтобы получить ситуацию, как будто холодный спай находиться при 0.
1.1) Для этого, мы просто умножаем «холодный спай» на некий коэффициент.
1.2) Коэффициент мы находим по формулам.
2) После этого, мы переводим значение «горячего спая» в температуру, умножая на некий другой коэффициент.
Г — горячий спай
Х — холодный
КТ — коэффициент термопары
температура = (Г + Х * Ч) * КТ
где Ч = С + К1 * Х + К2 * Г — коэффициент компенсации «холодного спая»
Честно говоря, ситуация для меня не прояснилась. Возможно я где-то сильно торможу 🙂
Вот ниже есть pdf. В тех расчетах все понятно — берем температуру холодного спая, через многочлен с заданными в таблице коэффициентами вычисляем ЭДС «холодного спая». Потом ЭДС «холодного» и «горячего» спая суммируем, и (через другой многочлен) приходим к температуре.
А вот в Вашем случае я не могу понять логику расчетов. Для начала не понятно — откуда возись цифры 28,7414 28,5902 30,9189 (каков их смысл).
Ели вы их как-то получили/вычислили экспериментально, то зачем вы сначала аппроксимируется результаты трех измерений к линейной функции, а потом, на основе этой функции, вычисляете значение для вашего 5-го эксперимента.
тем самым внося нелинейность в формулу перевода «попугаев» в температуру
Источник