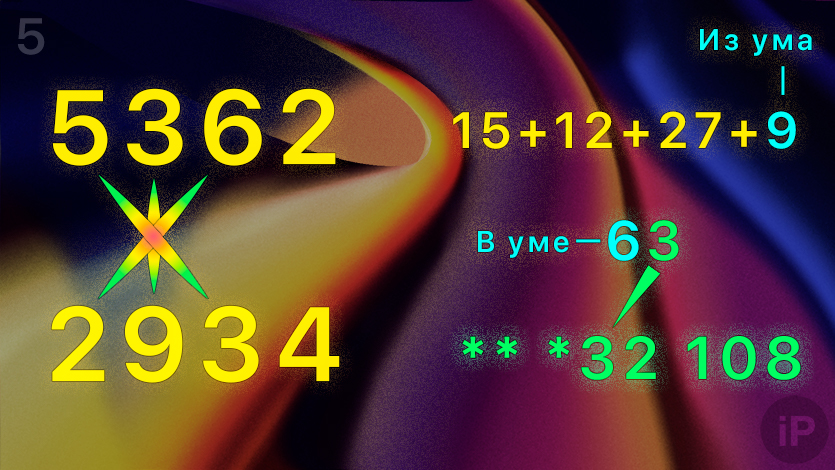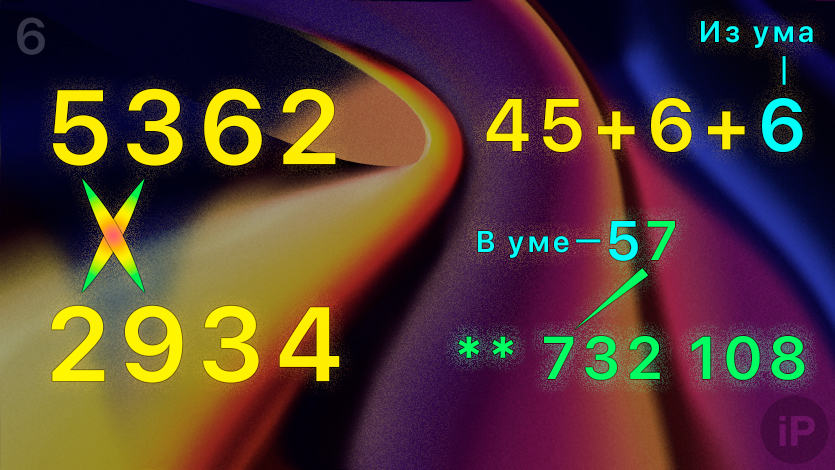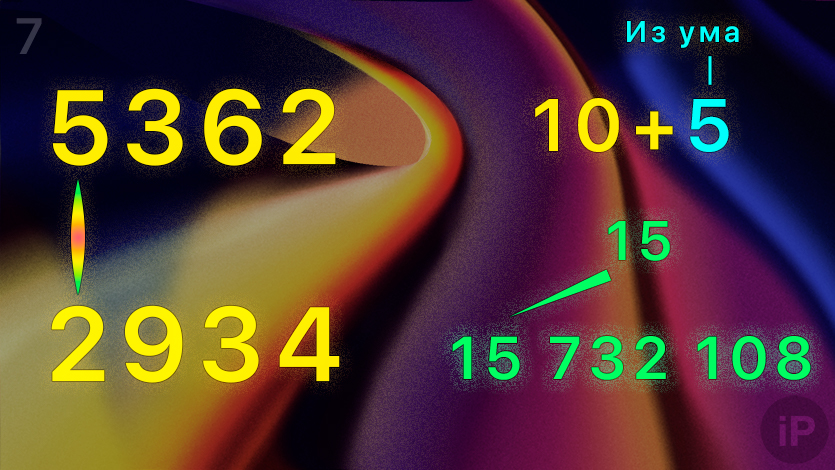Способ когда умножаешь систему

Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

В школе всё время слышал «где мне пригодится эта математика?».

И сам задавался таким вопросом. А сейчас вот не хватает учебника для «раскачки» извилин. Например, было бы заметно удобнее считать утерянные цены на Apple или выравнивать пиксельную сетку для иллюстраций.

Но не всё потеряно. Умножать числа в любом возрасте считают проверенным способом подточить ум и даже улучшить психическое здоровье.

Ниже расскажу, где оно ещё может пригодиться и что за секретный способ умножения прокачает ваше знание цифр до уровня интуиции.

Крупный счёт прокачает решение бытовых вопросов

Как любому компьютеру нужно расширять оперативную память, так и нашему мозгу нужен отсек для быстрых операций.

Тренировки с умножением укрепят краткосрочную память. Вы перестанете забывать, закрыли ли дверь на ключ, сколько яиц лежало в холодильнике перед походом в магазин и о чём вели речь после того, как отвлеклись.

Не говоря о том, что будете мгновенно считать, во сколько обойдётся вон тот сочный кусок мяса на шашлык или заправка автомобиля, чтобы доехать до соседнего города.

Вам нужна только математика начальной школы

Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

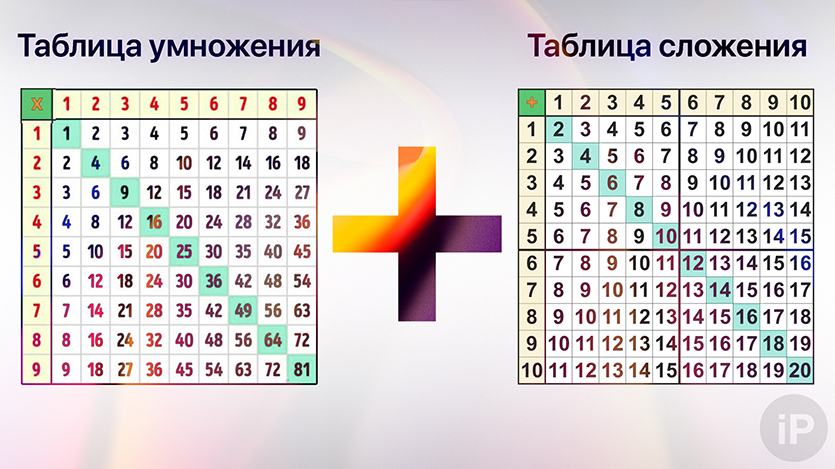
I. Знать таблицу умножения
II. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

8+5 = 8+2+3 = 10+3 = 13

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Операции с умножением тысячей в уме можно разделить на два типа: умножение на однозначные и многозначные числа.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

3864 = 3000 + 800 + 60 + 4

2. Умножаем каждый кусочек на второе число.

3000∙7 = 21000 | 800∙7 = 5600 | 60∙7 = 420 | 4∙7 = 28

3. Разбиваем результаты на простые группы одного размера.

21000 = 20000+1000 | 5600=5000+600 | 420 = 400+20 | 28 = 20+8

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 1000+5000 + 600+400 + 20+20 + 8

20000 + 6000 + 1000 + 40 + 8

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел . Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

0. Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

Источник

Счет в различных системах счисления

Сложение в системах счисления

Как мы складываем в десятичной системе счисления?

Давайте вспомним о том, как мы складываем числа уже привычным нам способом, в десятичной системе счисления.

Самое главное стоит понять разряды. Вспомните алфавит каждой СС и тогда вам станет легче.

Сложение в двоичной системе счисления

Сложение в двоичной системе ничем не отличается от сложения в десятичной системе. Главное помнить, алфавит содержит всего две цифры: 0 и 1. Поэтому когда мы складываем 1 + 1, то получаем 0, и увеличиваем число еще на 1 разряд. Посмотрите на пример выше:

1. Начинаем складывать как и привыкли справа налево. 0 + 0 = 0, значит записываем 0. Переходим к следующему разряду.
2. Складываем 1 + 1 и получаем 2, но 2 нет в двоичной системе счисления, а значит мы записываем 0, а 1 добавляем к следующему разряду.
3. У нас получается в этом разряде три единицы складываем 1 + 1 + 1 = 3, этой цифры также быть не может. Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.
4. У нас вновь получается 1 + 1 = 2. Мы уже знаем, что 2 быть не может, значит записываем 0, а 1 добавляем к следующему разряду.
5. Складывать больше нечего, значит в ответе получаем: 10100.

Один пример мы разобрали, второй решите самостоятельно:

Сложение в восьмеричной системе счисления

Так же как и в любых других системах счисления необходимо помнить Алфавит. Давайте попробуем сложить выражение.

1. Все как обычно, начинаем складывать справа налево. 4 + 3 = 7.
2. 5 + 4 = 9. Девяти быть не может, значит из 9 вычитаем 8, получаем 1. И еще 1 добавляем к следующему разряду.
3. 3 + 7 + 1 = 11. Из 11 вычитаем 8, получаем 3. И единицу добавляем к следующему разряду.
4. 6 + 1 = 7.
5. Складывать далее нечего. Ответ: 7317.

А теперь проделайте сложение самостоятельно:

Сложение в шестнадцатеричной системе счисления

1. Выполняем уже знакомые нам действия и не забываем про алфавит. 2 + 1 = 3.
2. 5 + 9 = 14. Вспоминаем Алфавит: 14 = Е.
3. С = 12. 12 + 8 = 20. Двадцати нет в шестнадцатеричной системе счисления. Значит из 20 вычитаем 16 и получаем 4. И единицу добавляем к следующему разряду.
4. 1 + 1 = 2.
5. Больше складывать нечего. Ответ: 24Е3.

Вычетание в системах счисления

Вычитание в десятичной системе счисления

Вспомним, как мы это делаем в десятичной системе счисления.

1. Начинаем слева направо, от меньшего разряда к большему. 2 – 1 = 1.
2. 1 – 0 = 1.
3. 3 – 9 = ? Тройка меньше девяти, поэтому позаимствуем единицу из старшего разряда. 13 – 9 = 4.
4. Из последнего разряда мы взяли единицу для предыдущего действия, поэтому 4 – 1 = 3.
5. Ответ: 3411.

Вычитание в двоичной системе счисления

1. Начинаем как обычно. 1 – 1 = 0.
2. 1 – 0 = 1.
3. От 0 отнять единицу нельзя. Поэтому заберем один разряд у старшего. 2 – 1 = 1.
4. Ответ: 110.

А теперь решите самостоятельно:

Вычитание в восьмеричной системе счисления

1. Ничего нового, главное помнить алфавит. 4 – 3 = 1.
2. 5 – 0 = 5.
3. От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 11 – 7 = 4.
4. Помним, что заимствовали единицу ранее, 6 – 1 = 5.
5. Ответ: 5451.

Пример для самостоятельного решения:

Вычитание в шестнадцатеричной системе счисления

Возьмем предыдущий пример, и посмотрим каков будет результат в шестнадцатеричной системе. Такой же или другой?

1. 4 – 3 = 1.
2. 5 – 0 = 5.
3. От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 19 – 7 = 12. В шестнадцатеричной системе 12 = С.
4. Помним, что заимствовали единицу ранее, 6 – 1 = 5
5. Ответ: 5С51

Пример для самостоятельного решения:

Умножение в системах счисления

Умножение в десятичной системе счисления

Давайте запомним раз и навсегда, что умножение в любой системе счисления на единицу, всегда даст тоже самое число.

1. Каждый разряд умножаем на единицу, как обычно справа налево, и получаем число 6748;
2. 6748 умножаем на 8 и получаем число 53984;
3. Проделываем операцию умножения 6748 на 3. Получаем число 20244;
4. Складываем все 3 числа, по правилам. Получаем 2570988;
5. Ответ: 2570988.

Умножение в двоичной системе счисления

В двоичной системе умножать очень легко. Мы всегда умножаем либо на 0, либо на единицу. Главное, это внимательно складывать. Давайте попробуем.

1. 1101 умножаем на единицу, как обычно справа налево, и получаем число 1101;
2. Проделываем эту операцию еще 2 раза;
3. Складываем все 3 числа внимательно, помним про алфавит, не забывая про лесенку;
4. Ответ: 1011011.

Пример для самостоятельного решения:

Умножение в восьмеричной системе счисления

Есть небольшой лайфхак, как считать в восьмеричной системе. Давайте рассмотрим на примере:

1. 5 х 4 = 20. А 20 = 2 х 8 + 4. Остаток от деления записываем в число – это будет 4, а 2 держим в уме. Проделываем эту процедуру справа налево и получаем число 40234;
2. При умножении на 0, получаем четыре 0;
3. При умножении на 7, у нас получается число 55164;
4. Теперь складываем числа и получаем – 5556634;
5. Ответ: 5556634.

Пример для самостоятельного решения:

Умножение в шестнадцатеричной системе счисления

Все как обычно, главное вспомните алфавит. Буквенные цифры, для удобства переводите в привычную для себя систему счисления, как умножите, переводите обратно в буквенное значение.

Давайте для наглядности разберем умножение на 5 числа 20А4.

1. 5 х 4 = 20. А 20 = 16 + 4. Остаток от деления записываем в число – это будет 4, а 1 держим в уме.
2. А х 5 + 1 = 10 х 5 + 1 = 51. 51 = 16 х 3 + 3. Остаток от деления записываем в число – это будет 3, а 3 держим в уме.
3. При умножении на 0, получаем 0 + 3 = 3;
4. 2 х 5 = 10 = А; В итоге у нас получается А334; Проделываем эту процедуру с двумя другими числами;
5. Помним правило умножения на 1;
6. При умножении на В, у нас получается число 1670С;
7. Теперь складываем числа и получаем – 169В974;
8. Ответ: 169В974.

Пример для самостоятельного решения:

Деление в системах счисления

С делением все так же, как и в привычной нам десятичной системе счисления.

Деление в двоичной системе счисления

В двоично системе счисления делить гораздо приятней, чем в десятичной системе. Потому что в десятичной надо угадывать числа и постоянно умножать, чтобы у нас получилось нужное значение. А в двоичной системе на какое еще число кроме единицы необходимо умножить, чтобы получить нужное значение? Правильно, ни на какое.

1. Сколько в 101 получится 11? Правильно, 1. 101 – 11 = 10;
2. 100 / 11? Так же 1 раз 11 поместится в 100. 100 – 11 = 1;
3. 11 / 11 = 1, в остатке 0;
4. Ответ: 111.

Деление в восьмеричной системе счисления

1. 46 меньше 53, значит делить будем 462. Надо угадать сколько раз число 53 поместиться? Угадываем 7 и записываем;
2. 53 / 53 = 1. Записываем к ответу, в остатке у нас 0;
3. Последний 0 мы так же записываем к ответу, так как делить больше нечего;
4. Ответ: 710.

Деление в шестнадцатеричной системе счисления

Осталось самое страшное – это научиться делить в шестнадцатеричной системе. Да прибудет с нами сила.

1. 4С мы должны поделить на 2В. Методом подбора определяем что умножить можем только 1 раз. 4С – 2В = 21 и единицу записываем в ответ;
2. Также методом подбора определяем, что 2В, мы можем умножить на С. 219 – 204 = 15;
3. Опять, методом подбора определяем, что это 8. 158 – 158 = 0, решение закончено;
4. Ответ: 1С8.

Источник