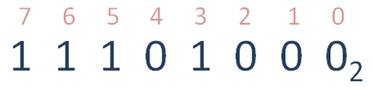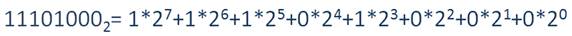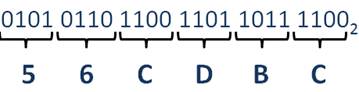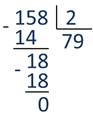Кодирование информации. Коды. Системы кодирования
Урок 4. Информатика 8 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Кодирование информации. Коды. Системы кодирования»
Для обмена информацией с другими людьми человек использует естественные и формальные языки. Представление информации с помощью какого-либо языка часто называют кодированием.
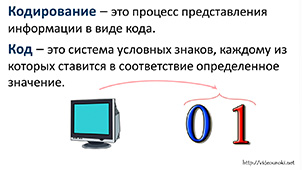
Кодирование — это процесс представления информации в виде кода.
Код — система условных знаков (символов), каждому из которых ставится в соответствие определенное значение.
Все множество символов, используемых для кодирования, называется алфавитом кодирования. Например, в памяти компьютера любая информация кодируется с помощью двоичного алфавита, содержащего всего два символа: 0 и 1.
Код состоит из определенного количества знаков, т. е. имеет определенную длину.
Количество знаков в коде называется длиной кода.
В процессе обмена информацией между людьми часто приходится переходить от одной формы представления информации к другой. Так, в процессе чтения вслух производится переход от письменной формы представления информации к устной и, наоборот, в процессе диктанта или записи объяснения учителя происходит переход от устной формы к письменной. В процессе преобразования информации из одной формы представления в другую происходит перекодирование информации.
Перекодирование — это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы.
Информация может быть представлена в форме числа, текста, графики или звука.
Средством перекодирования служит таблица соответствия знаковых систем (таблица перекодировки), которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Чаще всего кодированию подвергаются тексты на естественных языках. Существуют 3 основных способа кодирования текста:
1. графический — с помощью специальных рисунков или значков;
2. числовой — с помощью чисел;
3. символьный — с помощью символов того же алфавита, что и исходный текст.
Полный набор символов, используемый для кодирования текста, называется алфавитом или азбукой.
Рассмотрим некоторые способы кодирования.
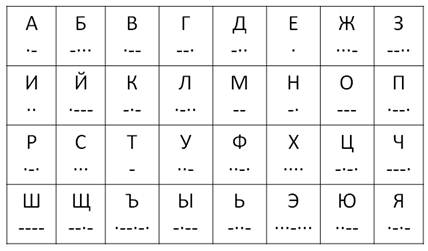
1. Кодированием информации с помощью букв русского алфавита. Суть этого способа заключается в том, чтобы каждую букву сообщения заменить ее номером в алфавите.
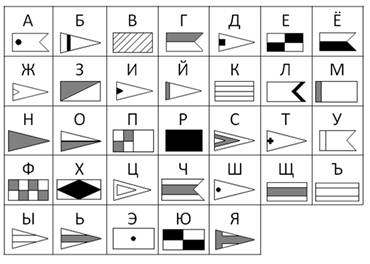
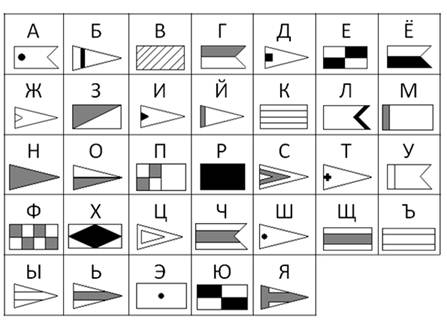
2. Флажковая азбука. При помощи этой азбуки осуществляется передача и прием сообщений между судами и кораблями в пределах прямой видимости. Здесь, каждой букве соответствует определенный флаг.
Информация кодируется тремя «буквами»:
· длинный сигнал (тире),
· короткий сигнал (точка),
· отсутствие сигнала (пауза) для разделения букв.
Таким образом, кодирование сводится к использованию набора символов, расположенных в строго определенном порядке.
4. Шифр Цезаря. Этот шифр реализует следующее преобразование текста: каждая буква исходного текста заменяется третьей после нее буквой в алфавите, которая считается написанным по кругу.
5. Перевод чисел из одной системы счисления в другую.
Пусть требуется перевести двоичное число в десятичную систему счисления.
Чтобы осуществлять перевод из двоичной системы счисления в десятичную, следует для начала пронумеровать разряды исходного числа справа налево, начиная с нуля.
Запишем число в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2:
И вычислив по правилам десятичной арифметики, получили число 232.
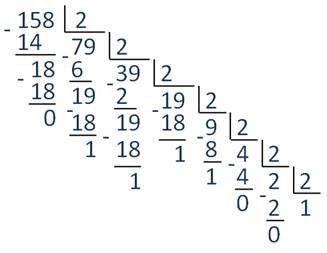
Пусть теперь требуется перевести двоичное число в восьмеричную систему счисления. Для этого следует разбить это двоичное число на триады, начиная с младшего бита.
Если старшая триада не заполнена до конца, как в нашем случае, следует дописать в ее старшие разряды нули. После этого необходимо заменить двоичные триады, начиная с младшей, на числа, равные им в восьмеричной системе. Это числа: 4, 7, 6, 6, 4, 5, 5, 2.
Таким образом, наше двоичное число запишется в виде:
Аналогично поступаем при переводе чисел из двоичной системы счисления в шестнадцатеричную, но разбиение двоичного числа производим на тетрады. Для примера будем использовать то же двоичное число, что и при переводе в восьмеричную систему счисления.
Заменяя двоичные тетрады на их шестнадцатеричные значения, то есть на C, B, D, C, 6, 5, получим искомое шестнадцатеричное число:
А теперь давайте мы попробуем перевести число 158 из десятичной в двоичную систему счисления. Для этого нужно выполнить последовательное деление нацело числа 158 на основании новой системы счисления, то есть на 2. Получим:
Далее число 79 делим на 2. Аналогичные действия выполняем до тех пор, пока частное не станет равным единице.
Затем запишем остатки от деления в обратном порядке, заменив их цифрами новой системы счисления, т.е. получили число 11101000.
При переводе числа из шестнадцатеричной системы счисления в двоичную, необходимо только заменить каждую цифру шестнадцатеричного числа ее эквивалентом в двоичной системе счисления (используя таблицу соответствия). И не забываем, что каждое шестнадцатеричное число следует заменять двоичным, дополняя его до 4 разрядов (в сторону старших разрядов).
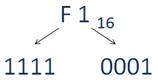
Пусть требуется перевести шестнадцатеричное число F1 в двоичное число. Воспользовавшись таблицей соответствия, получим:
F соответствуют четыре единицы в двоичной системе счисления, а 1 соответствует такая запись 0, 0, 0, 1 в двоичной системе счисления.
Итак, число F1 в двоичной системе счисления запишется так 11110001.
Пусть теперь нам нужно перевести число F1 из шестнадцатеричной системы счисления в восьмеричную. Обычно при таком переводе чисел вначале шестнадцатеричное число переводят в двоичное, затем разбивают его на триады, начиная с младшего бита, а потом заменяют триады соответствующими им эквивалентами в восьмеричной системе. В итоге у на получится, что исходному числу в восьмеричной системе счисления соответствует число 361.
Источник
Конспект «Кодирование информации. Способы кодирования.»
Информация может поступать от источника к приёмнику с помощью сигналов самой разной физической природы. Например, сигнал может быть световым, звуковым, тепловым, электрическим или в виде жеста, движения, слова, сломанной веточки на дереве, другого условного знака.
Для того чтобы произошла передача информации, приёмник информации должен не только получить сигнал, но и расшифровать его. Так, услышав звонок будильника, ученик понимает, что пришло время просыпаться и собираться в школу. Телефонный звонок означает, что кому-то нужно с вами поговорить.
Звонок в дверь сообщает, что кто-то пришёл, а школьный звонок собирает ребят на урок или оповещает их о долгожданной перемене.
Необходимо заранее договариваться, как понимать те или иные сигналы, другими словами, требуется разработка кода.
Код — это система условных знаков для представления информации. Кодирование — это представление информации с помощью некоторого кода.
Множество кодов очень прочно вошло в нашу жизнь. Так, для общения в нашей стране используется код — русский язык. Код используется для оценки знаний в школе (число 5 — код отличных знаний, 4 — код хороших знаний, 3 — удовлетворительных, 2 — плохих).
С помощью нотных знаков записывается (кодируется) любое музыкальное произведение. По номерному знаку можно узнать сведения об автомобиле и его владельце.
В современных супермаркетах каждый товар имеет на упаковке штрих-код — метку, состоящую из чёрных линий. Для чтения штрих-кодов применяют специальные сканеры. С их помощью в компьютер вводят информацию о стоимости покупки.
Правила дорожного движения кодируются с помощью наглядных символических рисунков. Всем хорошо известны следующие дорожные знаки, изображённые на рис. 15 (стр.47).
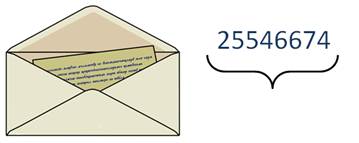
Свой код из шести цифр (почтовый индекс) имеет каждый населённый пункт Российской Федерации. Его следует писать на конверте в специально отведённом для этого месте (рис. 16, стр.48). По коду можно узнать, куда отправлять письмо. Например, код города Москвы и коды всех населённых пунктов Московской области начинаются с цифры 1.
В середине XIX века французский педагог Луи Брайль придумал специальный способ представления информации для слепых. «Буквы» этого кода выдавливаются на листе плотной бумаги. Одна буква занимает два столбика, в каждом из которых может быть выдавлено от одной до трёх точек (рис. 17, стр.48). Проводя пальцами по выступам, незрячие люди различают буквы и могут читать.
В памяти компьютера информация представлена в двоичном коде в виде цепочек нулей и единиц. Каждому символу, вводимому с клавиатуры, соответствует уникальная цепочка из восьми 0 и 1. Например, буква «Q» имеет двоичный код 01010001, а цифра «7» — 00110111.
Пример 1. Составим простейшую кодовую таблицу, поставив в соответствие каждой букве её порядковый номер в алфавите. Тогда скороговорка
в закодированном виде будет выглядеть так:
Пример 2. Можно закодировать информацию, заменяя каждую букву исходного текста, например, следующей после неё буквой в алфавите. Такой код называют шифром замены. В этом случае исходное сообщение
Способы кодирования информации.
Одна и та же информация может быть представлена разными кодами, иначе говоря, в разных формах.
Люди выработали множество форм представления информации. К ним относятся: разговорные языки (русский, английский, немецкий — всего более 2000 языков), язык мимики и жестов, язык рисунков и чертежей, научные языки (например, язык математики), языки искусства (музыка, живопись, скульптура), специальные языки (азбука Брайля, азбука Морзе, флажковая азбука).
Способ кодирования (форма представления) информации зависит от цели, ради которой осуществляется кодирование. Такими целями могут быть сокращение записи, засекречивание (шифровка) информации, удобство обработки и т. п.
Чаще всего применяют следующие способы кодирования информации:
1) графический — с помощью рисунков или значков;
2) числовой — с помощью чисел;
3) символьный — с помощью символов того же алфавита, что и исходный текст.
Переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки, также называют кодированием.
Действия по восстановлению первоначальной формы представления информации принято называть декодированием. Для декодирования надо знать код.
Любая, в том числе и графическая, информация может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них — числовую ось — вы уже рассматривали на уроках математики.
Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.
Нарисуем на листе в клетку две перпендикулярные числовые оси, точку их пересечения обозначим через О (рис. 18, стр.50).
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе — по оси OY. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси OY) (рис. 19, стр.50).
Посмотрите на шахматную доску (рис. 20, стр.51). Вдоль её нижнего края идёт ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями (рис. 21, стр.51).
Далее мы будем работать только в первой координатной четверти (рис. 22, стр.51).
Пример. Известны координаты 15 точек: А(4, 1), В(4, 2), С(1, 2), D(4, 5), Е(2, 5), F(4, 7), G(3, 7), Н(5, 9), 1(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А — В — С — D — Е — F — G — Н — I — J — К — L — М — N — О — А, то получим рисунок 23 (стр.52).
Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.
Источник