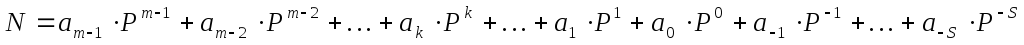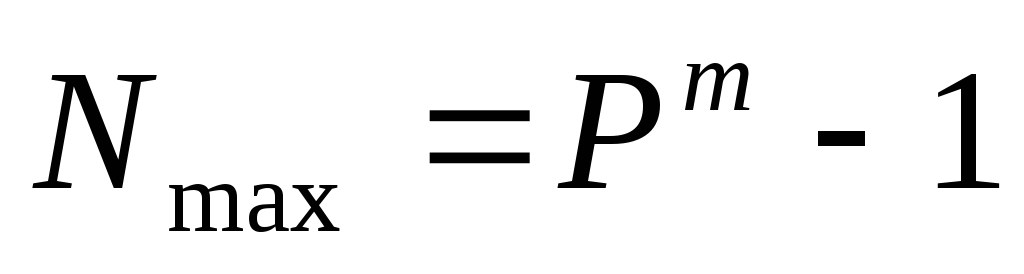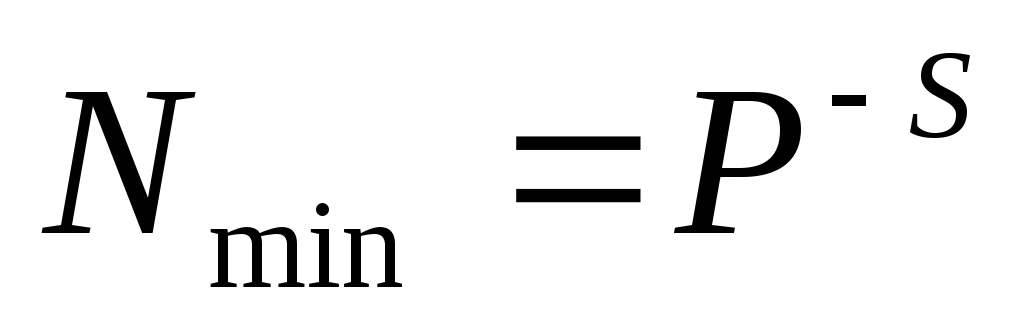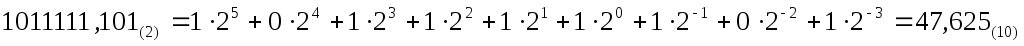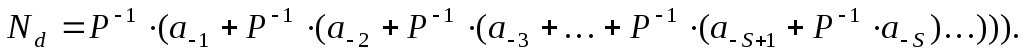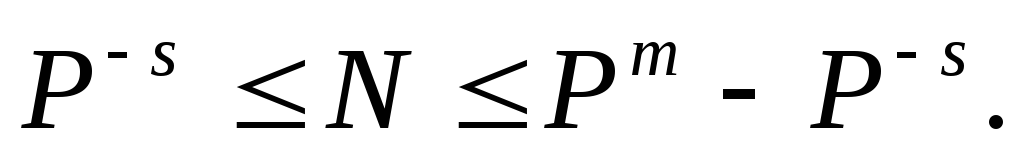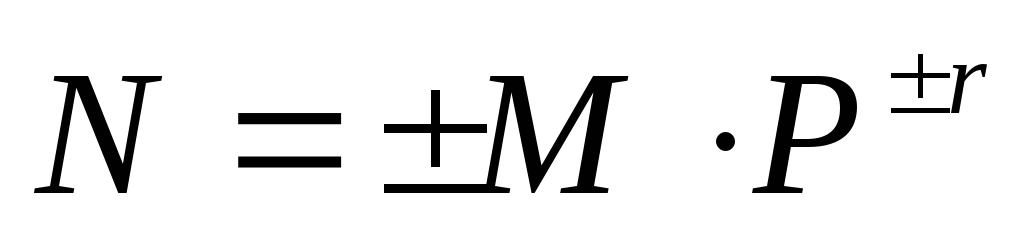- Лабораторная работа № 6 Инфологические основы эвм. Системы счисления. Перевод чисел.
- Теоретические сведения
- Перевод целых чисел. Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения
- Системы счисления. Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения
Лабораторная работа № 6 Инфологические основы эвм. Системы счисления. Перевод чисел.
Цель: Освоить способы изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения.
Теоретические сведения
Представление информации в вычислительных машинах. Информация в компьютере кодируется в двоичной или в двоично-десятичной системах счисления.
Система счисления — способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел, системы счисления делятся на следующие:
В позиционной системе счисления количественное значение каждой цифры завиит от ее места (позиции) в числе.
В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе.
Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до Р — 1.
В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида:
Нижние индексы определяют местоположение цифры в числе (разряд):
положительные значения индексов — для целой части числа (т разрядов);
отрицательные значения — для дробной (s разрядов).
Максимальное целое число, которое может быть представлено в т разрядах:
Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части:
Имея в целой части числа m, а в дробной — s разрядов, можно записать всего Р т+ S разных чисел.
Двоичная система счисления имеет основание Р = 2 и использует для представления информации всего две цифры: 0 и 1. Существуют правила перевода чисел из одной системы счисления в другую, основанные в том числе и на соотношении (1). Например, двоичное число 101111,101 равно десятичному числу 47,625.
Обратный перевод может быть выполнен значительно проще, если предварительно преобразовать отдельно целую и дробную части выражения (1) к виду:
Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием Р, основанный на этих выражениях, позволяет оперировать с числами в той системе счисления, из которой число переводится, и может быть сформулирован следующим образом.
При переводе смешанного числа следует переводить его целую и дробную части отдельно.
Для перевода целой части числа его, а затем целые части получающихся частных от деления следует последовательно делить на основание Р до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево, образуют целую часть числа в системе счисления с основанием Р.
Для перевода дробной части числа его, а затем дробные части получающихся произведений следует последовательно умножать на основание Р до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная разрядность дробной части числа. Целые части произведений, записанные после запятой последовательно слева направо, образуют дробную часть числа в системе счисления с основанием Р.
Рассмотрим перевод смешанного числа из десятичной в двоичную систему счисления на примере числа 47,625. Переводим целую часть числа:
47:2 = 23 (остаток 1)
23: 2 = 11 (остаток 1)
11:2 = 5 (остаток 1)
5:2 = 2 (остаток 1)
2:2 = 1 (остаток 0)
1:2 = 0 (остаток 1)
Записываем остатки последовательно снизу вверх — 101111, то есть 4710 = 101111
Переводим дробную часть числа:
Записываем целые части получающихся Произведений после запятой последовательно слева направо — 0,101, то есть 0,625 — 0,1012.
Окончательно 47,62510 = 101111,1012.
Представление чисел с фиксированной и плавающей запятой. В вычислительных машинах применяются две формы представления двоичных чисел:
естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой).
В форме представления с фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего не приемлема при вычислениях. Диапазон значащих чисел N в системе счисления с основанием Р при наличии т разрядов в целой части и 5 разрядов в дробной части числа (без учета знака числа) будет:
В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.
В форме представления с плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая — порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок — целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:
где М — мантисса числа (/М/ -300 до 10 300 . Для сравнения: количество секунд, которые прошли с момента образования планеты Земля, составляет всего 10 18 .
Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде; Нормализованным называют такое число, в старшем разряде мантиссы которого стоит единица. У нормализованных двоичных чисел, следовательно, 0,5
Абсолютная величина числа
Рис.1 Число с фиксированной запятой формата слово со знаком.
Рис.2 Число с плавающей запятой формата двойное слово
Двоично-кодированные десятичные числа могут быть представлены в ПК полями переменной длины в так называемых упакованном и распакованном форматах .
В упакованном формате для каждой десятичной цифры отводится по четыре двоичных разряда (полбайта), при этом знак числа кодируется в крайнем правом полубайте числа (1100 — знак «+» и 1101 — знак «-»).
Рис.3 Структура поля упакованного формата
Знак — Знак числа.
Упакованный формат используется обычно в ПК при выполнении операций сложения и вычитания двоично-десятичных чисел.
В распакованном формате для каждой десятичной цифры отводится по целому байту, при этом старшие полубайты (зона) каждого байта (кроме самого младшего) в ПК заполняются кодом 0011 (в соответствии с ASCII-кодом), а в младших (левых) полубайтах обычным образом кодируются десятичные цифры. Старший полубайт (зона) самого младшего (правого) байта используется для кодирования знака числа.
Рис.4 Структура поля распакованного формата
Распакованный формат используется в ПК при вводе-выводе информации, а также при выполнении операций умножения и деления двоично-десятичных чисел.
Например, число -19310 = -0001100100112-10 в ПК будет представлено:
в упакованном формате:
0001 1001 0011 1101
в распакованном формате:
0011 0001 0011 1001 1101 0011.
Код ASCII (American Standard Code for Information Interchange) — американский стандартный код для обмена информацией) имеет основной стандарт и расширение. Основной стандарт для кодирования символов использует шестнадцатеричные коды 00-7F, расширение стандарта — коды 80-FF.
Основной стандарт является международным и используется для кодирования управляющих символов и букв латинского алфавита; в расширении стандарта кодируются символы псевдографики и буквы национального алфавита (естественно, в разных странах разные). Пользоваться таблицей достаточно просто. Следует приписать шестнадцатеричную цифру номера строки справа к шестнадцатеричной цифре номера столбца. Так получится шестнадцатеричный код символа.
Наряду с кодом ASCII в ВС, в частности в сети Интернет, используется общий для всех стран мира универсальный код — Уникод (Unicode). Этот код основан на паре байт — машинном слове. Шестнадцати бит хватает для отображения 65 535 знаков. Такого количества достаточно для всех существующих алфавитов (то есть алфавиты большинства стран мира размещаются в основном стандарте этого кода).
Источник
Перевод целых чисел. Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения
ИНФОРМАЦИОННО-ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
Системы счисления
Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
Различают позиционные и непозиционные системы счисления. В позиционных системах каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:
, 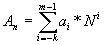
где ai – i-я цифра числа; k – количество цифр в дробной части числа; m — количество цифр в целой части числа; N – основание системы счисления.
Основание системы счисления N показывает, во сколько раз “вес” i-го разряда больше (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
Любое число Х в позиционной системе счисления можно записать как X+k p *M , где М – мантисса, Р- порядок. В ЭВМ с целью упрощения вычислений «.» фиксируется либо перед старшим либо после младшего разряда.
Пример 1.1.А10=37.25.
В соответствии с формулой (2.1)это число формируется из цифр с весами рядов:
Теоретически наиболее экономичной системой счисления является система с основанием е=2,71828. находящимся между числами 2 и 3.
Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено:
более простой реализацией алгоритмов выполнения арифметических и логических операций;
более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
экономичностью аппаратурной реализации всех схем ЭВМ.
При N=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления широкое распространение получили и производные системы:
• десятичная, точнее двоично-десятичное представление десятичных чисел, — <0, 1. 9>;
• шестнадцатеричная — <0,1,2, . 9, А, В, С, D, Е, F>. Здесь шестнадцатеричная цифра А обозначает число 10,В-число 11, . F-число 15;
• восьмеричная (от слова восьмерик) — <0,1,2,3,4,5, 6, 7>. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 16 = 2 4 и 8 = 2 3 . Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.
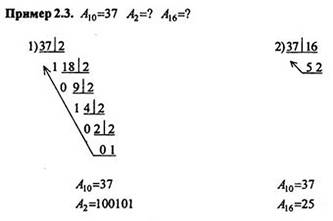
Перевод целых чисел
Целое число с основанием N1 переводится в систему счисления с основанием N2 путем последовательного деления числа An1, на основание N2 , записанного в виде числа с основанием N1, до получения остатка. Полученное частное следует вновь делить на основание N2, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя. Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основанием N2.
Проверку правильности перевода можно выполнить используя веса разрядов.
32 16 8 4 2 1 16 1
1 0 0 1 0 1 = 1+4+32 =37 2 5 =16*2+5=37
Так как восьмеричная и шестнадцатиричная системы являются производными от двоичной системы, то перевод может быть осуществлен еще более проще.
Для перевода числа из двоичной системы в восьмичичную, двоичное число разбивается на триады, и каждая двоичная триада записывается в виде десятичной цифры.
Для перевода числа из двоичной системы в шестнадцатеричную, двоичное число разбивается на тетрады и каждая двоичная тетрада записывается в виде десятичной цифры.
Источник
Системы счисления. Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения



Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
Различают позиционные и непозиционные системы счисления. В позиционных системах каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:
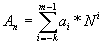
где ai – i-я цифра числа; k – количество цифр в дробной части числа; m — количество цифр в целой части числа; N – основание системы счисления.
Основание системы счисления N показывает, во сколько раз “вес” г-го разряда больше (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
В соответствии с формулой (1.1.1) это число формируется из цифр с весами рядов:
А10=3*10 1 +7*10 0 +2*10 -1 +5*10 -2 .
Теоретически наиболее экономичной системой счисления является система с основанием е=2,71828. находящимся между числами 2 и 3.
Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено:
более простой реализацией алгоритмов выполнения арифметических и логических операций;
более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
экономичностью аппаратурной реализации всех схем ЭВМ.
При N=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления широкое распространение получили и производные системы:
— десятичная, точнее двоично-десятичное представление десятичных чисел, — <0, 1. 9>;
— шестнадцатеричная — <0,1,2, . 9, А, В, С, D, Е, F>. Здесь шестнадцатеричная цифра А обозначает число 10,В-число 11, . F-число 15;
— восьмеричная (от слова восьмерик) — <0,1,2,3,4,5, б, 7>. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 16 = 2 4 и 8 = 2 3 . Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.
Пример 1.2. Число в двоичной, восьмеричной и шестнадцатеричной системах счисления имеет следующее представление:
A2=1*2 6 +1*2 5 +0*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 +1*2 -1 +0*2 -2 +1*2 -3 ;
A8=1*8 2 +4*8 1 +4*8 0 +5*8 -1 ;
A16=6*16 1 +4*16 0 +10*16 -1 .
Представление чисел в различных системах счисления допускает однозначное преобразование их из одной системы в другую. В ЭВМ перевод из одной системы в другую осуществляется автоматически по специальным программам. Правила перевода целых и дробных чисел отличаются.
Источник