МИ 2083-90 ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
ОПРЕДЕЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИИ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ
КОМИТЕТ СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ СССР
1. ОБЩИЕ ПОЛОЖЕНИЯ
2. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ
3. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ НЕЛИНЕЙНОЙ ЗАВИСИМОСТИ
4. МЕТОД ПРИВЕДЕНИЯ
5. ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ
ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РЕКОМЕНДАЦИИ
КРИТЕРИЙ ОТСУТСТВИЯ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ПОГРЕШНОСТЯМИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИИ АРГУМЕНТОВ
ГСИ. ИЗМЕРЕНИЯ КОСВЕННЫЕ
Определение результатов измерений и оценивание их погрешностей
Дата введения 01.01.92
Настоящая рекомендация распространяется на нормативно-техническую документацию, содержащую методики выполнения косвенных измерений, и устанавливает основные положения определения результатов измерений и оценивание их погрешностей при условии, что аргументы, от которых зависит измеряемая величина, принимаются за постоянные физические величины; известные систематические погрешности результатов измерений аргументов исключены, а неисключенные систематические погрешности распределены равномерно внутри заданных границ ± θ.
Термины и определения, используемые в настоящей рекомендации, приведены в приложении 1.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Искомое значение физической величины А находят на основании результатов измерений аргументов а1, . . . , а i , . . . , а m , связанных с искомой величиной уравнением
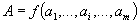
Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.
1.2. Результаты измерений аргументов и оценки их погрешностей могут быть получены из прямых, косвенных, совокупных, совместных измерений. Сведения об аргументах могут быть взяты из справочной литературы, технической документации.
1.3. При оценивании доверительных границ погрешностей результата косвенного измерения обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.
1.4. Основные положения рекомендации устанавливаются для оценивания косвенно измеряемой величины и погрешностей результата измерения:
при линейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 2);
при нелинейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 3);
для коррелированных погрешностей измерений аргументов при наличии рядов отдельных значений измеряемых аргументов (разд. 4).
Примечание. Критерий проверки гипотезы об отсутствии корреляции между погрешностями измерений аргументов приведен в приложении 2.
2. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ
2.1. Искомое значение A связано с m измеряемыми аргументами a 1 , a 2 , . . . , am уравнением
Корреляция между погрешностями измерений аргументов отсутствует.
Примечание. Если коэффициенты b 1 , b 2 . bm определяют экспериментально, то задача определения результата измерения величины решается поэтапно: сначала оценивают каждое слагаемое bi · ai ; как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины A .
2.2. Результат косвенного измерения 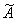
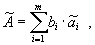
где 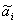
2.3. Среднее квадратическое отклонение результата косвенного измерения 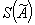
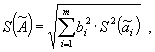
где 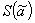
2.4. Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют (без учета знака) по формуле
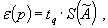
где tq , — коэффициент Стьюдента, соответствующий доверительной вероятности P = l — q и числу степеней свободы f эф , вычисляемому по формуле
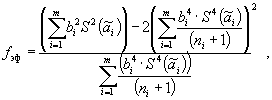
где ni , — число измерений при определении аргумента ai , .
2.5. Границы неисключенной систематической погрешности результата косвенного измерения вычисляют следующим образом.
2.5.1. Если неисключенные систематические погрешности результатов измерений аргументов заданы границами θ i ; то доверительные границы неисключенной систематической погрешности результата косвенного измерения Θ( p ) (без учета знака) при вероятности P вычисляют по формуле
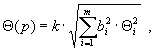
где k — поправочный коэффициент, определяемый .принятой доверительной вероятностью и числом m составляющих Θ i .
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.
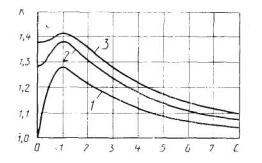
При доверительной вероятности Р = 0,99 поправочный коэффициент принимают равным 1,4, если число суммируемых составляющих m >4. Если же число составляющих m ≤4, то поправочный коэффициент k ≤1,4; более точное значение k можно найти с помощью графика зависимости
где m — число суммируемых составляющих (аргументов); l — параметр, зависящий от соотношения границ составляющих.
На графике кривая 1 дает зависимость k от l при m = 2, кривая 2 — при m = 3, кривая 3 — при m = 4.
Погрешность, возникающая при использовании формулы ( 7) для суммирования неисключенных систематических погрешностей, не превышает 5 % (расчеты получены на основе анализа результатов композиций равномерных распределений).
2.5.2. Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы доверительными границами, соответствующими вероятностям Pi , (границы неисключенных систематических погрешностей результатов измерений аргументов вычислены по формуле ( 7), то границы неисключенной систематической погрешности результата косвенного измерения для вероятности P вычисляют (без учета знака) по формуле
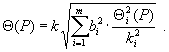
Для вероятности P = 0,95 ki = 1,1; для Р = 0,99 значения коэффициентов ki определяют в соответствии с п. 2.5.1.
2.6. Погрешность результата косвенного измерения оценивают на основе композиции распределений случайных и неисключенных систематических погрешностей.
2.6.1. Если 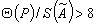
2.6.2. Если 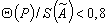
2.6.3. Если 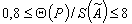
где K — коэффициент, зависящий от доверительной вероятности и от отношения 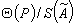
Значения коэффициента K в зависимости от отношения 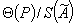
Источник
8.6 Особенности измерения силы токов
8.6 Особенности измерения силы токов
Существует ряд методов измерения силы токов в электрических цепях:
кроме прямых измерений, широко используются косвенные измерения.
Прямое измерение силы тока. В этом случае амперметр включают последовательно в разрыв электрической цепи (рис. 8.18, а), в которой производится измерение силы тока.
Включение в исследуемую цепь амперметра искажает результат измерения. В частности, наличие в схеме рис. 8.18, а амперметра с внутренним сопротивлением Ra приведет к тому, что вместо силы тока Ix = U /R, который протекал в этой цепи без амперметра, после его включения потечет ток:
Абсолютная погрешность измерения △I = Ix – I1 будет тем больше, чем выше внутреннее сопротивление амперметра Ra .
Измерение силы тока косвенным методом с помощью электронных вольтметров. Поскольку между напряжением и током в электрической цепи имеется линейная связь (согласно закону Ома), то ток может быть измерен косвенным методом с помощью схемы, показанной на рис. 8.18, б. При этом, измерив вольтметром напряжение на сопротивлении эталонного резистора Rэ силу тока находим по формуле:
где Uэ — напряжение, измеренное вольтметром; Ix — ток, подлежащий опре- делению; Rэ — активное эталонное сопротивление известного номинала.
Однако при измерении малых токов подобная методика может оказать неприемлемой. В этом случае в измерительных приборах применяется cxeма входного усилительного каскада с достаточно малым входным сопротивлением.Одним из вариантов такого каскада может служить преобразователь тока в напряжение.
Особенности измерений малых токов и напряжений. Рассмотренные способы измерения напряжения или токов малых уровней основаны, главным образом, на применении усилителей. Для усиления малых сигналов требуется иметь усилитель с большим коэффициентом усиления. Современный уровень развития электронной техники позволяет успешно решить эту задачу. Поэтому не коэффициент усиления, а внутренние шумы источника и усилителя исследуемого сигнала определяют предельно достижимый порог чувствительности при измерении малых уровней сигналов.
Источник
Методы измерений
Метод измерений – прием или совокупность приемов сравнения измеряемой величины с ее единицей или шкалой в соответствии с реализованным принципом измерений.
По общим приемам получения результатов измерений методы различают на:
- прямой метод измерений – измерение, при котором искомое значение величины находят непосредственно из опытных данных. Прямые измерения не требуют методики проведения измерений и проводятся по эксплуатационной документации на применяемое средство измерений;
- косвенный метод измерений – измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью. Косвенные измерения применяются в случаях, когда невозможно выполнить прямые измерения, например при определении плотности твердого тела, вычисляемой по результатам измерений объема и массы.
По условиям измерения:
- контактный метод измерений – основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (измерение температуры тела термометром);
- бесконтактный метод измерений – основан на том, что чувствительный элемент прибора не приводится в контакт с объектом измерения (измерение расстояния до объекта радиолокатором, измерение температуры в доменной печи пирометром).
Исходя из способа сравнения измеряемой величины с ее единицей, различают:
- метод непосредственной оценки – метод при котором значение величины определяют непосредственно по отсчетному устройству показывающего СИ (термометр, вольтметр и пр.). Мера, отражающая единицу измерения, в измерении не участвует. Ее роль играет в СИ шкала, проградуированная при его производстве с помощью достаточно точных СИ.
- метод сравнения с мерой – метод при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (измерение массы на рычажных весах с уравновешиванием гирями). Существует три разновидности этого метода:
- нулевой метод – метод сравнения с мерой, в котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля, например, измерения электрического сопротивления мостом с полным его уравновешиванием;
- метод замещения – основан на сравнении с мерой, при котором измеряемую величину замещают измвестной величиной, воспроизводимой мерой, сохраняя все условия неизменными, например взвешивание c поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов;
- метод совпадений – метод сравнения с мерой, в котором разность между значениями искомой и воспроизводимой мерой величин измеряют, используя совпадения отметок шкал или периодических сигналов, например при измерении с использованием штангенциркуляс нониусом наблюдают совпадение меток на шкалах штангенциркуля и нониуса;
- дифференциальный метод – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
- метод совпадений – метод измерений, при котором определяют разность между измеряемой величиной и величиной воспроизводимой мерой, используя совпадение отметок шкал или периодических сигналов. Примером этого метода является измерение длины при помощи штангенциркуля с нониусом. Метод совпадений часто применяется при измерениях параметров периодических процессов.
Поскольку погрешность определяется не только метрологическими характеристиками средств измерений, но и погрешностью отбора и приготовления проб, условиями проведения измерений, ошибкой оператора и другими причинами, это определение означает, что методики выполнения измерений могут разрабатываться и быть аттестованными только применительно к конкретным условиям проведения измерения с использованием конкретных средств.
Данное утверждение не означает, что для каждой измерительной или испытательной лаборатории должны разрабатываться собственные методики. Но если лаборатория использует тип средства измерения, приведенный в аттестованной методике, влияющие факторы (температура и влажность окружающего воздуха и измеряемой среды, напряжение и частота электрической сети, вибрация, внешнее магнитное поле и др.) находятся в определенном данной методикой диапазоне, а оператор соответствует установленной в ней квалификации, то физические величины будут измеряться в этой лаборатории с известной погрешностью.
Источник