Способ измерения площади палеткой

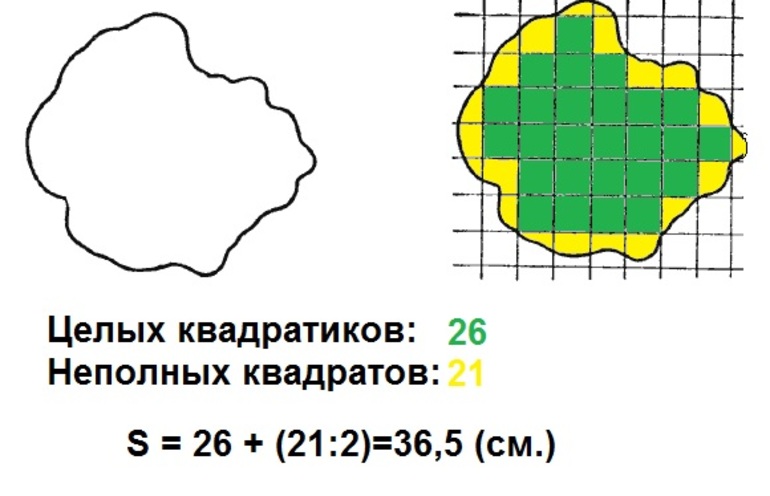
Измерение площадей палетками

Площади небольших участков с криволинейными граница­ми можно измерять с помощью палеток. Палетка для измере­ния площадей – лист прозрачного материала (восковки, лавса­на, пластика, кальки), на который нанесена сетка квадратов размером 2×2 мм или система равноотстоящих параллельных линий.

Наложив палетку с сеткой квадратов на план, подсчиты­вают число квадратов, уместившихся в измеряемой площади, оценивая дробные части квадратов на краях участка на глаз. Результат подсчета умножают на площадь одного квадрата.

Так, квадрату размером 2×2 мм на плане масштаба 1:1000 соответствует на местности квадрат 2×2 м, то есть площадь равная 4 м 2 . Если подсчитанное число квадратиков равно 122,4, то площадь участка равна 122,4 · 4 м 2 = 490 м 2 .

Рис. 5.1 Палетка с параллельными линиями

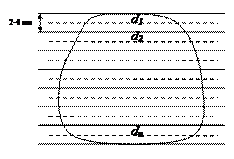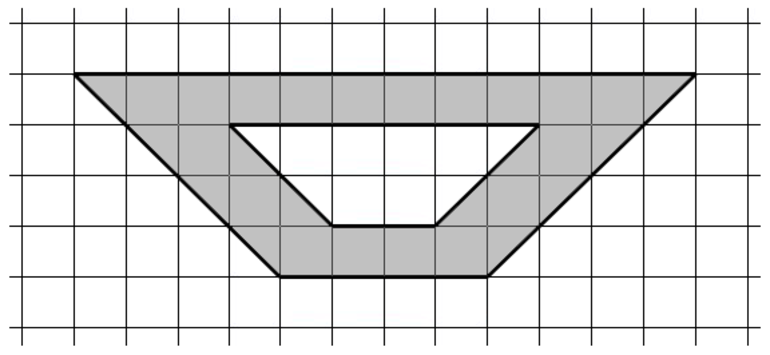
Для измерения площади палеткой с параллельными линия­ми ее накладывают на план так, чтобы противоположные края участка расположились посредине между линиями палетки (рис. 5.1).

Отрезки линий палетки, ограниченные контуром участка, можно рассматривать как средние линии трапеций, заключенных на рисунке между пунктирными линиями. Из­мерив длины средних линий d₁, d₂, . d_n, площадь участка вычисляют по формуле (5.1):

где h — расстояние между линиями палетки (в масштабе).

Определение суммы отрезков d₁ + d₂ + … + d_n выполняют циркулем-измерителем. Взяв в раствор измерителя отрезок d₁, переносят измеритель на следующую линию, на продолжение отрезка d₂ и увеличивают раствор так, что в растворе будет набрана сумма d₁ + d₂. Продолжая, накапливают всю сумму расстояний и определяют ее значение по масштабной линейке.

Прямоугольная палетка построена в виде сетки квадратов. Определение площади прямоугольной палеткой выполняют по способу А.Н. Савича (рис.5.2).

Способ А. Н. Савича применяется при измерении на плане больших площадей. Часть Р₀ площади участка (рис. 5.2), состоящая из целых квадратов, образованных линиями координатной сетки, не требует измерения – она равна сумме известных площадей квадратов. Измеряют площади Р₁, Р₂, Р₃, Р₄, расположенные на краях участка и составленные

нецелыми частями квадратов. Вся измеряемая площадь равна

Рис. 5.2 Измерение площади способом Савича

Р = Р₀ + Р₁ + Р₂ + Р₃+ Р₄. (5.2)

Измерение площадей Р₁, Р₂, Р₃, Р₄ может быть выполнено любым из описанных выше методов (по координатам, по линейно-угловым измерениям).

Рис. 5.3 К способу Савича

Для повышения точности измерения площадей Р₁, Р₂, Р₃ и Р₄ рекомендуется измерять еще и дополнения этих площа­дей до целых квадратов и окончательные их значения вычис­лять. Пусть, например, непосредственное измерение площади Р₁ дало результат R (рис. 5.3). Измерением площади, дополняющей R до пяти целых квадратов, получен результат Q. Если бы не погрешности измерений и деформации бумаги, то сумма R + Q равнялась бы точно P_Q – площади прямоуголь­ника, состоящего из пяти квадратов. Полагая погрешности пропорциональными размерам измеряемых площадей, напишем пропорцию , откуда следует . (5.3)

Достоинством способа Савича является то, что значитель­ная часть площади (а именно – Р₀) определяется без измере­ний, аналитически. Уменьшение измеряемой части площади и выполнение измерений с контролем повышают точность оп­ределения площади. Кроме того, оказывается учтенной дефор­мация бумаги.

Если значительная часть площади составлена целыми квад­ратами, а измерять приходится лишь малую ее часть, точность способа Савича близка к точности аналитических способов.

5.2 Способы определения площади участка с криволинейными границами

Источник

Математика. 4 класс

Конспект урока

Математика, 4 класс

Урок №14. Измерение площади фигуры с помощью палетки

Перечень вопросов, рассматриваемых в теме:

Площадь геометрической фигуры.

Вычисление площади фигур произвольной формы, используя палетку.

Глоссарий по теме:

Площадь — свойство фигур занимать место на плоскости.

Длина — свойство предмета “быть протяжённым в пространстве”

Палетка — прозрачная пластинка, разделенная на единицы площади.

Основная и дополнительная литература по теме урока:

1. Математика: 4 класс: учебник в 2 ч. Ч.1/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение, 2016. – с. 36-38
2. Всероссийские проверочные работе. Математика. Рабочая тетрадь 4 класс в 2 ч. Ч 1/ под.ред. Н.А. Сопруновой – М.; Просвещение, 2016. – с. 50 -68

Теоретический материал для самостоятельного изучения

Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.

Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см 2

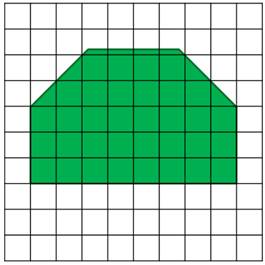
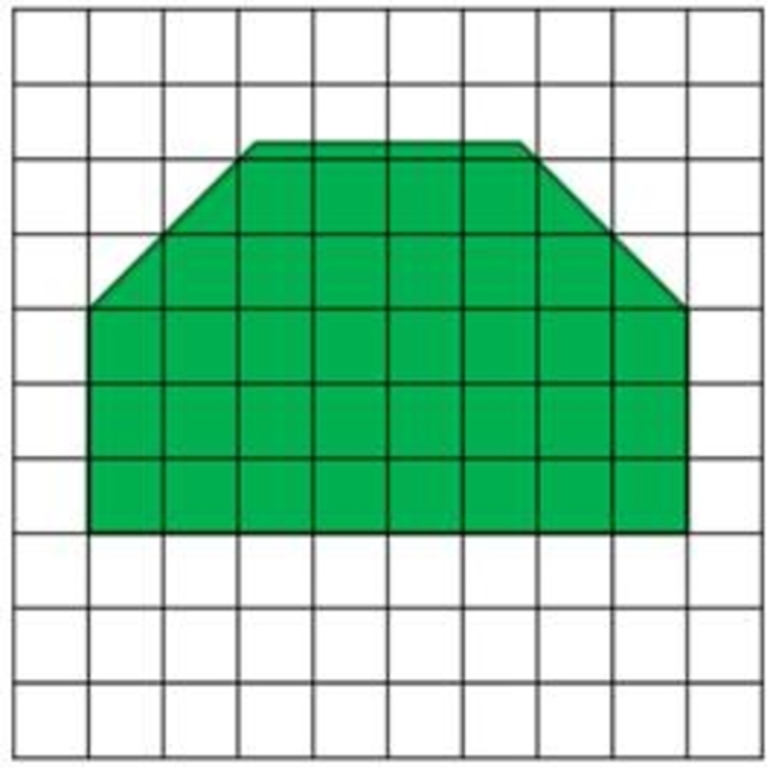
А теперь попробуйте вычислить площадь данной фигуры:

-?

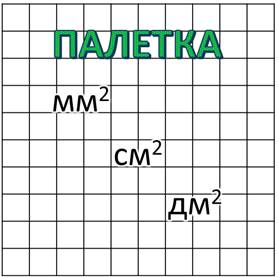
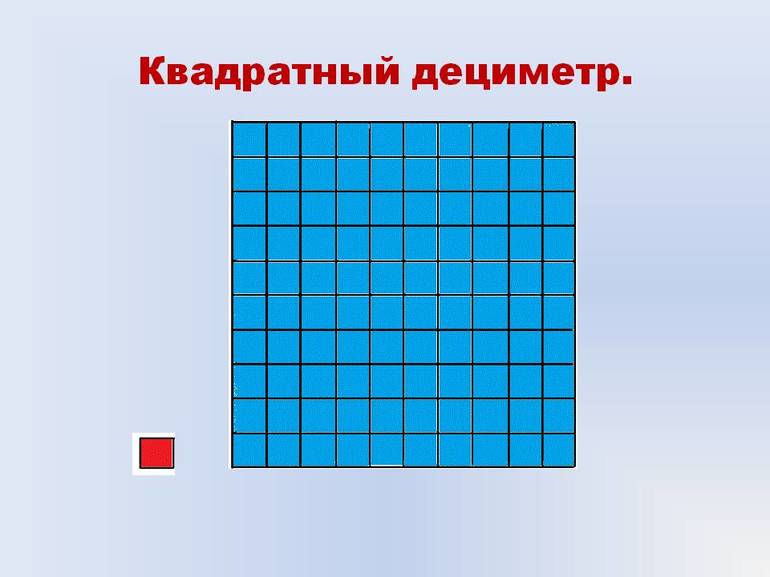
Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка — лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:

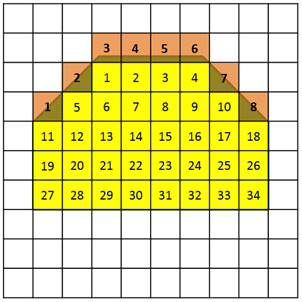
1) На данную фигуру наложить палетку. Не сдвигать!

2)Сосчитать, сколько целых клеток- квадратных единиц — содержится в фигуре.

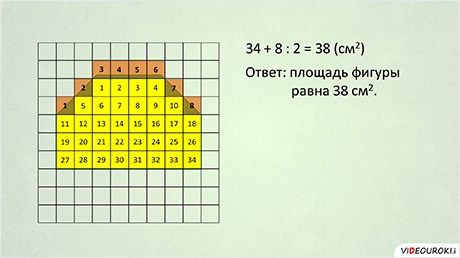
Целых 34 клетки.

3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

Неполных 8 клеток.

4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.

5) Сложить числа, полученные в пунктах 2 и 4.

6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.

S = 34 + (8 : 2) = 38 см 2

Ответ: S = 38 см 2

Задания тренировочного модуля:

1. Определите, какая фигура имеет большую площадь, а какая — меньшую, и решите ребус соответствия.

Правильный ответ: Прямоугольник – большую, круг – меньшую.

Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Источник

Палетка. Измерение площади фигуры с помощью палетки

Урок 7. Математика 4 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Палетка. Измерение площади фигуры с помощью палетки»

Вы знаете, я хотела узнать площадь нашей страны, но мне это не сразу удалось сделать. Дело в том, что её границы имеют неправильную форму – это не прямоугольник, не квадрат, и даже не круг.

Я обратилась за помощью к нашей царице, и она рассказала мне, как находить площадь любой, самой искривлённой фигуры. Царица дала мне вот такое простое приспособление. Это прозрачная пластина или плёнка с разлиновкой в клеточку. Называется она – палетка. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры или квадратные дециметры.

Представьте себе, что надо узнать площадь вот такой фигуры.

Накладываем на неё палетку.

Сначала считаем, сколько всего целых квадратиков. Их тридцать четыре. Теперь считаем все оставшиеся кусочки. Их восемь. Люди договорились, что каждые два кусочка засчитывают за один полный квадратик. Поэтому количество кусочков делим на два. Получилось четыре.

Складываем тридцать четыре и четыре. Это тридцать восемь. Значит, площадь этой фигуры – примерно тридцать восемь квадратиков.

Так как в школе чаще всего пользуются палетками, разделёнными на квадратные сантиметры, то вы бы сказали, что площадь данной фигуры примерно равна тридцати восьми квадратным сантиметрам. Почему примерно? Потому что площадь фигуры по палетке вряд ли возможно определить абсолютно точно, ведь редко два кусочка могут идеально заменить целый квадратик.

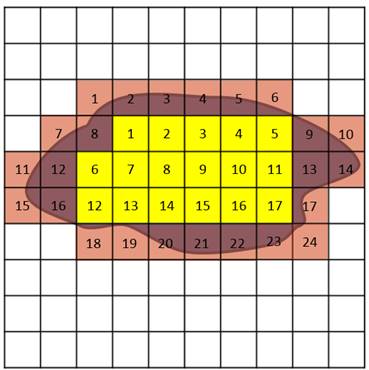
А теперь попробуем найти площадь вот такой, совершенно бесформенной фигуры.

Опять накладываем на неё палетку. Считаем целые квадратики.

Их семнадцать. Теперь считаем кусочки. Их двадцать четыре. Количество кусочков делим на два и полученное число прибавляем к семнадцати. Получилось примерно двадцать девять квадратных сантиметров.

Иногда случается и так, что количество кусочков – нечётное число, например, тринадцать или двадцать пять. Тогда делим на два ближайшее чётное число, больше данного на один. Ведь всё равно при помощи палетки точно площадь фигуры измерить невозможно. А вот почему берём чётное число больше данного, вы узнаете в пятом классе.

Запомнили, ребята, как мы определяем площадь фигур с помощью палетки?

̶ Накладываем палетку на фигуру.

̶ Считаем количество целых квадратов.

̶ Считаем количество кусочков.

̶ Количество кусочков делим на два…

̶ Складываем полученное число с количеством целых квадратов….

̶ Записываем ответ.

Видите, всё просто!

Кстати, именно так, используя план местности и палетку, можно найти площадь участка земли, или озера, или целого города, и даже страны. Вот этим я сейчас и займусь. Пока, ребята!

Источник

Палетка для математики — модели изготовления и правила использования

Методы изготовления

Для математических вычислений площади сложных фигур правильно использовать заводской набор. В инструкции от производителя школьник может найти следующую информацию: для чего нужна палетка по математике, из каких материалов она изготовлена, как нужно её использовать. Внешне модель выглядит, как прозрачная пластина либо плёнка с разлиновкой в клетку.

С учётом параметров фигуры, площадь которой необходимо найти, образец разделяется на квадратные миллиметры, сантиметры, дециметры. Некоторые фирмы производят подобные инструменты с магнитной основой. Выбор зависит от предпочтений ребёнка и условий задачи.

Но можно сделать палетку по математике и своими руками.

Для этого потребуются следующие материалы:

Если предстоит работа с маленькими величинами, рекомендуется воспользоваться миллиметровой бумагой. Внешне самодельная палетка схожа на заводскую — расчерчена на клетки гибкого листа, предназначенного для нахождения площадей неправильных и правильных фигур, а также выполнения иных упражнений.

Самостоятельный шаблон будет стоить дешевле, чем заводской.

Кроме перечисленных материалов, потребуется прозрачная плотная полиэтиленовая обложка для дневника или тетради. Нужно измерить ее и расчертить ручкой на квадраты со сторонами 1 см. Данный шаблон будет иметь размеры 10х10 см. Если для изготовления применяется миллиметровка, рекомендуется обклеить её сверху скотчем, повторно расчертив клетки. Таким способом продлевается срок эксплуатации инструмента и дополнительно он защищается от влаги.

Чтобы сделать палетку площадью в 100 кв. см, потребуется придерживаться следующего алгоритма:

• На листе в клетку отображается схема инструмента.
• На палетку накладывается обложка.
• Правильно обводятся клеточки. Чтобы инструмент выглядел аккуратно, используется линейка.
• Вырезается готовый шаблон.

Рекомендации по использованию

Процесс измерения площади с помощью палетки простой, если она изготовлена правильно. Инструмент нужно приблизить к фигуре, наложив его сверху, и произвести расчет целых и неполных квадратов. Сложнее пользоваться палеткой, если все точки плоскости не поместились в неё.

В таком случае рекомендуется придерживаться следующего метода:

• Разделить фигуру на части.
• Произвести подсчёт каждой части отдельно.
• Найти суммарный результат.

Рекомендуется подсчитывать отдельно, сколько целых квадратов вмещается в фигуру и сколько неполных. Площадь фигуры вычисляется по специальной формуле: S = количество целых квадратов (количество неполных/2). На уроках математики в начальной школе рекомендуется использовать палетку в виде прозрачного листка, на который нанесена сетка с квадратами (стороны по 1 см). Это объясняется тем, что в младших классах ученики работают с фигурами небольших размеров.

В современных учебниках по математике описаны подробные шаги по изготовлению и применению палетки. Рекомендуется использовать лист из тетради в клеточку. Из него вырезается самостоятельно школьником квадрат со сторонами 10х10 и ячейками в 1 см. Такой инструмент значительно упрощает работу, связанную с вычислением площадей фигур с неровными краями.

Очертания полученного шаблона обводятся чёрным маркером. Им же осуществляется дополнительная разметка составных квадратиков. Предполагается, что подобный метод значительно упростит и ускорит вычисления. Школьнику будет легко и просто посчитать количество полных и неполных квадратов. Полученная палетка оборачивается с двух сторон скотчем либо самоклеющейся обложкой.

За счёт использования маркера отсутствует необходимость в повторной обводке прозрачного шаблона.

Чтобы школьнику было удобно понять, как получается математическое значение, палетку нужно наложить на неровно очерченную поверхность и подсчитать количества полных и неполных квадратов. В современных учебниках по математике первого понятие обозначается буквой P, а второе — N. Общий вид формулы: S=PxN/2.

Другой вариант записи: S=N+M/2, где

• N — целые квадраты.
• M — неполные квадраты.

Необходимо учесть, что полученный результат считается приблизительным, так как площадь и размер неполных квадратиков разная.

Примеры вычислений

В математике встречаются фигуры с неправильными границами, к примеру, овал. Для вычисления его площади понадобится палетка. Её нужно наложить сверху, подсчитав квадраты внутри границ овала. Предварительно подсчитывается количество целых клеток. Их вышло 34.

Кусочков насчитывается 8. Так как 8 — чётное число, поэтому два неполных квадрата можно засчитать за один целый. Если восемь разделить на два, получится четыре. Если к 34 добавить 4, получится 38. Площадь овала будет примерно равна 38 квадратиков или 38 квадратных сантиметров.

Задача: на тетрадь разлились чернила, появилось пятно. Чтобы выяснить, сколько клеток запачкалось, используется палетка. Так как пятно не имеет чёткой формы, поэтому накладывается сверху шаблон. При подсчёте выходит 17 целых клеток и 24 неполных.

Последнее число делится на два. К результату добавляется 17. Получается около 29 квадратных сантиметров. Другого алгоритма рекомендуется придерживаться, если количество клеток нечётное, к примеру, 30 либо 25. В таком случае на два нужно разделить ближайшую чётную цифру, но больше данного значения на единицу.

Моря и земельные участки

Палетка часто используется учениками на уроках географии. Чтобы найти площадь моря или озера, рекомендуется найти географический атлас либо карту с максимально возможным масштабом. Математический инструмент прикладывается к объекту. Выполняются следующие шаги:

• Считаются целые квадраты.
• Затем — неполные.
• Последний результат делится на два.
• Полученное число суммируется с количеством целых квадратиков.
• Записывается ответ.

Можно воспользоваться схемой и для расчёта площади страны, земельного участка, города. Чтобы выяснить примерную площадь местности, потребуется миллиметровая бумага. На ней с помощью карандаша приблизительно рисуется контур участка. Масштаб можно подобрать самостоятельно.

Современные педагоги и психологи считают, что с помощью палетки у детей формируется умение добывать информацию из текста. Дополнительно ученики начальной школы учатся формулировать и аргументировать свои мысли. За счёт шаблона развиваются вычислительные навыки при подсчёте площади разных геометрических фигур.

Плюсы развития операции логического мышления:

Используя палетку, ребёнок учится анализировать свою деятельность. Одновременно развиваются действия самоконтроля, взаимоконтроля, прививается аккуратность, точность при построении разных фигур. Палетка помогает ученикам научиться записывать правильно площадь, переводить одни единицы в другие, решать математические и географические задачи.

С её помощью дети учатся работать с геометрическими фигурами, соблюдая порядок выполняемых действий в числовых выражениях со скобками либо без них.

Источник