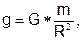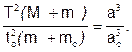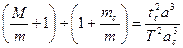Способ измерения массы небесного тела

Способ измерения массы небесного тела

§ 58. Определение масс небесных тел

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.

Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.

Первый способ применим пока только к Земле и заключается в следующем.

На основании закона тяготения ускорение силы тяжести на поверхности Земли

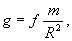
где т — масса Земли, a R — ее радиус. Отсюда масса Земли

Ускорение силы тяжести g (точнее, ускорение составляющей силы тяжести, обусловленной только силой притяжения), так же как и радиус Земли R , определяется из непосредственных измерений на поверхности Земли (см. § 46 и 62). Постоянная тяготения f достаточно точно определена из опытов Кэвендиша и Йолли, хорошо известных в физике.

С принятыми в настоящее время значениями величин g , R и f по формуле (2.25) получается масса Земли

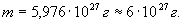
Зная массу Земли и ее объем, легко найти среднюю плотность Земли. Она равна 5,52 г/см 3

Третий, уточненный закон Кеплера позволяет определить соотношение между массой Солнца и массой планеты, если у последней имеется хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг нее.

Действительно, движение спутника вокруг планеты подчиняется тем же законам, что и движение планеты вокруг Солнца и, следовательно, уравнение (2.24) может быть записано в этом случае так:

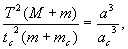
где — М, т и m_c — массы Солнца, планеты и ее спутника, Т и t_c — периоды обращений планеты вокруг Солнца и спутника вокруг планеты, a и а_с — расстояния планеты от Солнца и спутника от планеты соответственно.

Разделив числитель и знаменатель левой части дроби этого уравнения па т и решив его относительно масс, получим

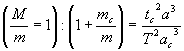
Отношение для всех планет очень велико; отношение же наоборот, мало (кроме Земли и ее спутника Луны) и им можно пренебречь. Тогда в уравнении (2.26) останется только одно неизвестное отношение , которое легко из него определяется. Например, для Юпитера определенное таким способом обратное отношение равно 1 : 1050.

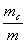
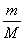
Так как масса Луны, единственного спутника Земли, сравнительно с земной массой достаточно большая, то отношением 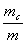в уравнении (2.26) пренебрегать нельзя. Поэтому для сравнения массы Солнца с массой Земли необходимо предварительно определить массу Луны. Точное определение массы Луны является довольно трудной задачей, и решается она путем анализа тех возмущений в движении Земли, которые вызываются Луной.

Под влиянием лунного притяжения Земля должна описывать в течение месяца эллипс вокруг общего центра масс системы Земля — Луна.

По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые “лунным неравенством”. Наличие “лунного неравенства” в видимом движении Солнца указывает на то, что центр Земли действительно описывает небольшой эллипс в течение месяца вокруг общего центра масс “Земля — Луна”, расположенного внутри Земли, на расстоянии 4650 км от центра Земли. Это позволило определить отношение массы Луны к массе Земли, которое оказалось равным 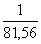. 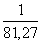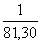Положение центра масс системы “Земля — Луна” было найдено также из наблюдений малой планеты Эрос в 1930—1931 гг. Эти наблюдения дали для отношения масс Луны и Земли величину . Наконец, по возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось равным . Последнее значение наиболее точное, и в 1964 г. Международный астрономический союз принял его как окончательное в числе других астрономических постоянных. Это значение подтверждено в 1966 г. вычислением массы Луны по параметрам обращения ее искусственных спутников.

С известным отношением масс Луны и Земли из уравнения (2.26) получается, что масса Солнца M _¤ в 333 000 раз больше массы Земли, т.е.

Зная массу Солнца и отношение этой массы к массе любой другой планеты, имеющей спутника, легко определить массу этой планеты.

Массы планет, не имеющих спутников (Меркурий, Венера, Плутон), определяются из анализа тех возмущений, которые они производят в движении других планет или комет. Так, например, массы Венеры и Меркурия определены по, тем возмущениям, которые они вызывают в движении Земли, Марса, некоторых малых планет (астероидов) и кометы Энке — Баклунда, а также по возмущениям, производимым ими друг на друга.

Источник

§9.4. Определение масс небесных тел

Масса — одна из важнейших характеристик небесных тел. Но как можно определить массу небесного тела? Ньютон доказал, что более точная формула третьего закона Кеплера такова:

где М₁ и М₂ — массы каких-либо небесных тел, а m₁, и m₂ — соответственно массы их спутников. В частности, планеты являются спутниками Солнца. Мы видим, что уточненная формула этого закона отличается от приближенной наличием множителя, содержащего массы Если под М₁ = М₂ = М понимать массу Солнца, а под m₁ и m₂ — массы двух разных планет, то отношение

будет мало отличаться от единицы, так как m₁ и m₂ очень малы по сравнению с массой Солнца. При этом точная формула не будет заметно отличаться от приближенной.

Уточненный третий закон Кеплера позволяет определить массы планет, имеющих спутников, и массу Солнца. Чтобы определить массу Солнца, перепишем формулу этого закона в следующем виде, сравнивая движение Луны вокруг Земли с движением Земли вокруг Солнца:

где T_з и а_з — период обращения Земли (год) и большая полуось ее орбиты, Т_л и а_л — период обращения Луны вокруг Земли и большая полуось ее орбиты, M_с — масса Солнца, M_з — масса Земли, m_л — масса Луны. Масса Земли ничтожна сравнительно с массой Солнца, а масса Луны мала (1:81) сравнительно с массой Земли. Поэтому вторые слагаемые в суммах можно отбросить, не делая большой ошибки. Решив уравнение относительно M_с/M_з имеем:

Эта формула позволяет определить массу Солнца, выраженную в массах Земли. Она составляет около 333 000 масс Земли.

Для сравнения масс Земли и другой планеты, например Юпитера, надо в исходной формуле индекс 1 отнести к движению Луны вокруг Земли массой М₁ а 2 — к движению любого спутника вокруг Юпитера массой М₂.

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они своим притяжением производят в движении соседних с ними планет или в движении комет и астероидов.

1. Определите массу Юпитера сравнением системы Юпитера со спутником с системой Земля — Луна, если первый спутник Юпитера отстоит от него на 422 000 км и имеет период обращения 1,77 сут. Данные для Луны должны быть вам известны.
2. Вычислите, на каком расстоянии от Земли на линии Земля — Луна находятся те точки, в которых притяжения Землей и Луной одинаковы, зная, что расстояние между Луной и Землей равно 60 радиусам Земли, а массы Земли и Луны относятся как 81 : 1.

Источник

Методы определения масс небесных тел.

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:

где m — масса Земли, а R — её радиус.

g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли:

m = 5,976 .1027г = 6 .1024кг.

Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.

2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас— расстояния планеты от Солнца и спутника от планеты соответственно.

Из уравнения следует

Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.

Соотношение М/m можно легко найти из уравнения.

Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.

3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые «лунным неравенством». Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс «Земля — Луна», расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг.

По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30.

В 1964 году Международный астрономический союз принял его как const.

Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.

Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.

Дата добавления: 2014-12-17 ; просмотров: 6762 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Способ измерения массы небесного тела

Коэффициент пропорциональности G = наз. гравитационной постоянной или постоянной тяготения. Её находят из физического эксперимента с крутильными весами, позволяющими определить силу гравитац. взаимодействия тел известной массы.

В случае свободного падения тел сила F, действующая на тело, равна произведению массы тела на ускорение свободного падения g. Ускорение g может быть определено, напр., по периоду T колебаний вертикального маятника: , где l — длина маятника. На широте 45 o и на уровне моря g= 9,806 м/с 2 .

Подстановка выражения для сил земного притяжения в ф-лу (1) приводит к зависимости , где — масса Земли, а — радиус земного шара. Таким путём была определена масса Земли г. Определение массы Земли явл. первым звеном в цепи определений масс др. небесных тел (Солнца, Луны, планет, а затем и звёзд). Массы этих тел находят, опираясь либо на 3-й закон Кеплера (см. Кеплера законы ), либо на правило: расстояния к.-л. масс от общего центра масс обратно пропорциональны самим массам. Это правило позволяет определить массу Луны. Из измерений точных координат планет и Солнца найдено, что Земля и Луна с периодом в один месяц движутся вокруг барицентра — центра масс системы Земля — Луна. Расстояние центра Земли от барицентра равно 0,730 (он расположен внутри земного шара). Ср. расстояние цeнтpa Луны от центра Земли составляет 60,08 . Отсюда отношение расстояний центров Луны и Земли от барицентра равно 1/81,3. Поскольку это отношение обратно отношению масс Земли и Луны, масса Луны
г.

Массу Солнца можно определить, применив 3-й закон Кеплера к движению Земли (вместе с Луной) вокруг Солнца и движению Луны вокруг Земли:
, (2)
где а — большие полуоси орбит, T — периоды (звёздные или сидерические) обращения. Пренебрегая по сравнению с , получим отношение , равное 329390. Отсюда г, или ок. .

Аналогичным путём определяют массы планет, имеющих спутников. Массы планет, не имеющих спутников, определяют по возмущениям, к-рые они оказывают на движение соседних с ними планет. Теория возмущённого движения планет позволила заподозрить существование тогда неизвестных планет Нептуна и Плутона, найти их массы, предсказать их положение на небе.

Массу звезды (помимо Солнца) можно определить со сравнительно высокой надёжностью только в том случае, если она явл. физ. компонентом визуально-двойной звезды (см. Двойные звезды ), расстояние до к-рой известно. Третий закон Кеплера в этом случае даёт сумму масс компонентов (в ед. ):
,
где а» -большая полуось (в секундах дуги) истинной орбиты спутника вокруг главной (обычно более яркой) звезды, к-рую в этом случае считают неподвижной, Р — период обращения в годах, — параллакс системы (в секундах дуги). Величина даёт большую полуось орбиты в а. е. Если можно измерить угловые расстояния компонентов от общего центра масс, то их отношение даст величину, обратную отношению масс: . Найденная сумма масс и их отношение позволяют получить массу каждой звезды в отдельности. Если компоненты двойной имеют примерно одинаковый блеск и сходные спектры, то полусумма масс даёт верную оценку массы каждого компонента и без дополнит. определения их отношения.

Для др. типов двойных звезд (затменно-двойных и спектрально-двойных) имеется ряд возможностей приблизительно определить массы звёзд или оценить их нижний предел (т.е. величины, меньше которых не могут быть их массы).

Совокупность данных о массах компонентов примерно ста двойных звёзд разных типов позволила обнаружить важную статистич. зависимость между их массами и светимостями (см. Масса-светимость зависимость ). Она даёт возможность оценивать массы одиночных звёзд по их светимостям (иначе говоря, по их абс. звёздным величинам ). Абс. звёздные величины М определяются по ф-ле: M = m + 5 + 5 lg — A(r) , (3) где m — видимая звёздная величина в выбранном оптич. диапазоне (в определённой фотометрич. системе, напр. U, В или V; см. Астрофотометрия ), — параллакс и A(r) — величина межзвёздного поглощения света в том же оптич. диапазоне в данном направлении до расстояния .

Если параллакс звезды не измерен, то приближённое значение абс. звёздной величины можно определить по её спектру. Для этого необходимо, чтобы спектрограмма позволяла не только узнать спектральный класс звезды, но и оценить относительные интенсивности нек-рых пар спектр. линий, чувствительных к «эффекту абс. величины». Иначе говоря, сначала необходимо определить класс светимости звезды — принадлежность к одной из последовательностей на диаграмме спектр-светимость (см. Герцшпрунга-Ресселла диаграмма ), а по классу светимости — её абс. величину. По полученной таким образом абс. величине можно найти массу звезды, воспользовавшись зависимостью масса-светимость (этой зависимости не подчиняются лишь белые карлики и пульсары ).

Ещё один метод оценки массы звезды связан с измерением гравитац. красного смещения спектр. линий в её поле тяготения. В сферически-симметричном поле тяготения оно эквивалентно доплеровскому красному смещению , где — масса звезды в ед. массы Солнца, R — радиус звезды в ед. радиуса Солнца, а выражено в км/с. Это соотношение было проверено по тем белым карликам, к-рые входят в состав двойных систем. Для них были известны радиусы, массы и истинные лучевые скорости v_r, являющиеся проекциями орбитальной скорости.

Невидимые (тёмные) спутники, обнаруженные около нек-рых звёзд по наблюдённым колебаниям положения звезды, связанным с её движением около общего центра масс (см. Невидимые спутники звезд ), имеют массы меньше 0,02 . Они, вероятно, не явл. самосветящимися телами и больше похожи на планеты.

Из определений масс звёзд выяснилось, что они заключены примерно в пределах от 0,03 до 60 . Наибольшее количество звёзд имеют массы от 0,3 до 3 . Ср. масса звезд в ближайших окрестностях Солнца , т.е. 10 33 г. Различие в массах звёзд оказывается много меньшим, чем их различие в светимостях (последнее может достигать десятков млн.). Сильно отличаются и радиусы звёзд. Это приводит к разительному различию их ср. плотностей: от до г/см 3 (ср. плотность Солнца 1,4 г/см 3 ).

Массу рассеянного звёздного скопления можно определить, сложив массы всех его членов, светимости к-рых определяют по их видимому блеску и расстоянию до скопления, а массы — по зависимости масса-светимость.

Массу шарового звёздного скопления далеко не всегда можно оценить путём подсчёта звёзд, т.к. в центральной области большинства таких скоплений изображения отдельных звёзд на фотографиях, полученных с оптимальной экспозицией, сливаются в одно светящееся пятно. Есть методы оценки общей массы всего скопления, основанные на статистич. принципах. Так, напр., применение теоремы о вириале (см. Вириала теорема ) позволяет оценить массу скопления (в ) по радиусу скопления r (пк) и ср. квадратич. отклонению лучевой скорости отдельных звёзд (в км/с) от ср. её значения (т.е. от лучевой скорости скопления как целого):
.

Если же подсчёт звёзд — членов шарового скопления возможен, то общую массу скопления можно определить как сумму произведений , где — функция светимости этого скопления, т.е. число звёзд, приходящихся на различные интервалы абс. звёздных величин M_i (обычно их подсчитывают в интервалах, равных 1 m ), a — масса, соответствующая данной абс. звёздной величине M_i по зависимости масса-светимость. Т.о., общая масса скопления , где сумма взята от самых ярких до самых слабых членов скопления.

Метод определения массы Галактики исходит из факта вращения Галактики. Устойчивость вращения позволяет предположить, что центростремит. ускорение для каждой звезды, в частности для Солнца, определяется притяжением вещества Галактики в пределах солнечной орбиты. Солнце притягивается к галактич. центру с силой , где R₀ — расстояние Солнца от ядра Галактики, равное см. Сила F₀ сообщает Солнцу ускорение , к-рое равно центробежному ускорению Солнца (без учёта влияния внеш. части Галактики и при условии эллипсоидальности поверхностей равной плотности по внутр. её части). Собственная галактич. скорость Солнца (т.н. круговая скорость на расстоянии R₀ от центра) 220 км/с, отсюда см/с 2 . Масса Галактики, без учёта её частей, внешних по отношению к галактической траектории Солнца, г. Масса Галактики в сферич. объёме с радиусом 15 кпк, согласно подобным расчётам, равна . При этом учитывается также масса всей диффузной (рассеянной) материи в Галактике.

Масса спиральной галактики может быть определена по результатам изучения её вращения, напр. из анализа кривой лучевых скоростей, измеренных в различных точках большой оси видимого эллипса галактики. В каждой точке галактики центростремит. сила пропорциональна массе более близких к центру галактики областей и зависит от закона изменения плотности галактики с удалением от её центра. Спектроскопич. наблюдения в оптич. диапазоне позволили построить кривые вращения спиральных галактик до расстояний 20-25 кпк от центра (а у ряда галактик высокой светимости до 40 кпк и более). Вплоть до этих расстояний круговая скорость не уменьшается с увеличением R, т.е. масса галактики продолжает расти с расстоянием. Т.о., в галактиках имеется скрытая масса . Масса невидимого (несветящегося) вещества галактик может в 10 и более раз превосходить массу светящегося вещества; предположительно, скрытая масса может существовать в форме очень слабых маломассивных звёзд или чёрных дыр или в форме элементарных частиц (напр., нейтрино , если они обладают массой покоя).

Для медленно вращающихся галактик, какими явл., напр., эллиптич. галактики, трудно получить кривые лучевых скоростей, но зато можно по расширению спектр. линии оценить ср. скорость звёзд в системе и, сопоставив её с истинными размерами галактики, определить её массу. Чем больше ср. скорость звёзд, тем больше должна быть масса галактики (при одинаковых размерах). Зависимость между массой, размерами галактики и ср. скоростью звёзд вытекает из условия стационарности системы.

Ещё один способ оценки массы галактик-компонентов двойных систем аналогичен методу оценки масс компонентов спектрально-двойных звёзд (ошибка не превышает 20%). Используют также установленную статистич. зависимость между массой и интегр. светимостью галактик различного типа (своего рода зависимость масса-светимость для галактик). Светимость определяется по видимой интегр. звёздной величине и расстоянию, к-рое оценивается по красному смещению линий в спектре. Ср. масса галактик, входящих в скопление галактик, оценивается по числу галактик скопления и его общей массе, к-рую статистически определяют по дисперсии лучевых скоростей галактик, подобно тому как оценивается общая масса звёздного скопления на основе теоремы о вириале.

Известные ныне массы галактик заключены в пределах от

10 5 (т.н. карликовые галактики) до 10 12 (сверхгигантские эллиптич. галактики, напр. галактика М 87), т.е. отношение масс галактик доходит до 10 7 .

Точность определения масс астрономич. объектов зависит от точности определения всех величин, входящих в соответствующие ф-лы. Масса Земли определена с погрешностью 0,05%, масса Луны 0,1%. Погрешность определения массы Солнца также составляет 0,1%, она зависит от точности определения астрономической единицы (ср. расстояния до Солнца). Вообще, в значит. степени точность определения массы зависит от точности измерения расстояния до космического объекта , в случае двойных звёзд — от расстояния между ними, от линейных размеров тел и т.д. Массы планет известны с погрешностью от 0,05 до 0,7%. Массы звёзд определены с погрешностью от 20 до 60%. Неуверенность определения масс галактик можно характеризовать коэфф. 2-5 (масса может быть в неск. раз больше или меньше), если надёжно определено расстояние до них.

Лит.:
Струве О., Линде Б., Пилланс Э., Элементарная астрономия, пер. с англ., 2 изд., М., 1967; Сагитов М.У., Постоянная тяготения и масса Земли, М., 1969; Климишин И.А., Релятивистская астрономия, М., 1983.

Источник