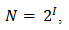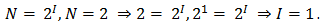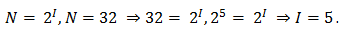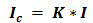Способ измерения информации алфавитный подход
Вокруг нас везде и всюду происходят информационные обмены. Информацией обмениваются между собой люди, животные, технические устройства, органы человека или животного и т.д. во всех этих случаях передача информации происходит в виде последовательностей различных сигналов. В вычислительной технике такие сигналы кодируют определенные смыс ловые символы, т.е. такие сигналы кодируют последовательности знаков — букв, цифр, кодов цвета точек и т.д. С этой точки зрения рассматривается другой подход к измерению информации — алфавитный.
Каким образом в этом случае можно найти количество информации?
канал передачи информации
Формула связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. Тогда в рассматриваемой ситуации N — это количество знаков в алфавите знаковой системы, а I — количество информации, которое несет каждый знак: N = 2 I .
С помощью этой формулы можно, например, определить количество информации, которое несет знак в двоичной знаковой системе:
Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению количества информации).
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.
В русской письменной речи частота использования букв в тексте различна, так в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в сто раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» — наибольшая).
Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации Iс в сообщении можно подсчитать, умножив количество информации I3, которое несет один знак, на длину кода (количество знаков в сообщении) К:
Информация и информационные процессы
Так, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут информацию в 2 бита, три цифры — в 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.3).
Количество информации, которое несет двоичный компьютерный код.
Двоичный компьютерный код
Символов на нашей клавиатуре около 200 (русский и латинский алфавит, строчные и прописные буквы, цифры, знаки препинания, спецсимволы). Попробуем подобрать число n, достаточное для кодирования этих символов: 27 = 128 (мало), 28 = 256 (хватит). Поэтому в кодировке ASCII 1 символ текста кодируется одним байтом (8 битами).
Количество данных, обрабатываемых компьютером, измеряется в байтах, но чаще для этого используются более крупные единицы:
1 Килобайт (Кб) = 2 10 байт = 1024 байт
1 Мегабайт (Мб) = 2 10 Кб = 1 048 576 байт
1 Гигабайт (Гб) = 2 10 Мб = 1 073 741 824 байт.
Может возникнуть вопрос, почему в международной системе СИ приставки Кило, Мега и Гига вдруг получили другое значение. Ответ здесь в больших буквах. Кило и кило — это две большие разницы.
1 килобайт (кб) = 10 3 байт = 1 000 байт
1 мегабайт (мб) = 10 6 байт = 1 000 000 байт
1 гигабайт (гб) = 10 9 байт = 1 000 000 000 байт.
В ноябре 2000 г. международной электротехнической комиссией (МЭК) были приняты поправки к международному стандарту. По этому решению приставки, кратные степеням 2 получили своё особое название:
1 кибибайт (Киб)= 2 10 байт = 1024 байт
1 мебибайт (Миб) = 2 10 Киб = 1 048 576 байт
1 гибибайт (Гиб)= 2 10 Миб = 1 073 741 824 байт
К сожалению, эти приставки не стали привычными нашему слуху, хотя срок их существования уже достаточно большой.
Постановлением Правительства Российской Федерации от 31 октября 2009 г. № 879 закреплено обозначение двоичных приставок в привычном звучании, но написание их отличается от десятичных.
Скорость передачи данных и пропускную способность каналов связи принято измерять в битах в секунду (бит/с) и кратных этому:
1 килобит (кбит/с) = 10 3 бит/с
1 мегабит (мбит/с) = 10 6 бит/с
1 гигабит (гбит/с) = 10 9 бит/с
А при измерении оперативной памяти принято измерение в единицах, кратных не степеням десятки, а степеням двойки.
Из-за этого первоначально и возникла путаница в приставках.
Источник
Алфавитный подход к определению количества информации
Цели урока:
1) Обучающая: рассмотреть алфавитный подход к измерению количества информации, научиться вычислять количество информации с точки зрения алфавитного подхода.
2) Развивающая: развитие у учащихся самостоятельности и познавательной активности.
3) Воспитывающая: воспитывать дисциплинированность, аккуратность, собранность.
Литература:
1) Угринович Н. Д. «Информатика 8 класс»,
2) Заславская О. Ю., Левченко И. В. «Информатика: весь курс».
1) Угринович Н. Д. «Информатика 8 класс».
Тип урока: ознакомление с новым материалом
План урока:
1. Организационный этап.
2. Актуализация знаний.
3. Подготовка учащихся к усвоению нового материала.
4. Этап получения новых знаний.
5. Этап обобщения и закрепления нового материала.
7. Заключительный этап.
Ход урока
1. Организационный этап.
Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
1) В чём заключается содержательный подход к измерению информации? (Количество информации — мера уменьшения неопределённости знаний при получении информационных сообщений.)
2) Какую минимальную единицу информации используют для измерения количества информации? (Бит)
3) Какую формулу используют для определения количества информации? (Формулу Хартли)
4) Производится бросание симметричной четырехгранной пирамидки. Какое количество информации мы получаем в зрительном сообщении о ее падении на одну из граней? (2 бита)
6) Из непрозрачного мешочка вынимают шарики с номерами и известно, что информационное сообщение о номере шарика несет 5 битов информации. Определите количество шариков в мешочке. (35)
3. Этап получения новых знаний.
Скачать видеоурок «Алфавитный подход к определению количества информации»
Содержательный подход к измерению информации рассматривает информацию с точки зрения человека, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не воспринимает содержание информации. Поэтому в вычислительной технике используется другой подход к определению количества информации. Он называется алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, пропуск между словами.
Алфавит — это множество символов, используемых при записи текста.
Мощность (размер) алфавита — это полное количество символов в алфавите.
Мощность алфавита обозначается буквой N.
· мощность алфавита из русских букв равна 33;
· мощность алфавита из латинских букв — 26;
· мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания );
· мощность двоичного алфавита равна 2.
При алфавитном подходе считается, что каждый символ текста имеет информационную емкость. Информационная емкость знака зависит от мощности алфавита.
Алфавит, с помощью которого записано сообщение состоит из N знаков. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений, которое будет нести количество информации I.
Тогда в формуле
N — количество знаков в алфавите знаковой системы, I — количество информации, которое несет каждый знак.
Например, из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе
Информационная емкость знака двоичной знаковой системы составляет 1 бит.
Задача 1. Определите, какое количество информации несет буква русского алфавита (без буквы ё).
Буква русского алфавита несет 5 битов информации.
Формула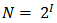 
связывает между собой количество возможных событий и количество информации, которое несёт полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите, знаковой системы, а I — количество информации, которое несёт один знак.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно посчитать, умножив количество информации, которое несет один знак на количество знаков в сообщении.
где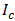 
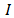
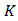
— количество информации в сообщении
— количество информации, которое несет один знак
— количество знаков в сообщении
Давайте решим с вами задачу.
Задача 2. Какое количество информации содержит слово «ПРИВЕТ», если считать, что алфавит состоит из 32 букв?
Решение. Что нам требуется найти в данной задаче? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».
Что нам для этого дано?
Дано: количество знаков в сообщение и мощность алфавита.
Количество знаков в сообщении равно 6, а мощность данного алфавита равна 32.
Что нам нужно найти? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».
Посмотрим на наше сообщение, оно содержит несколько знаков, значит для того чтобы найти количество информации нашего сообщения, нам нужно умножив количество информации, которое несет один знак, на количество знаков в сообщении, воспользоваться формулой «и» суммарное равно «и» умножить на «к».
Но мы еще не можем воспользоваться формулой, т.к. не знаем какое количество информации несет один знак. Для этого воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна 32, N равно 32. Мы получили уравнение. Решив это уравнение, мы получили, что количество информации, которое несет один знак нашего алфавита, равно 5 бит. Зная количество информации, которое несет один знак нашего алфавита, и количество знаков в сообщении, мы можем найти какое количество информации содержит наше сообщение.
Итак, наше сообщение содержит 30 бит.
4. Этап обобщения и закрепления нового материала.
1) Какое количество информации содержит слово «ИНФОРМАТИКА», если считать, что алфавит состоит из 32 букв? (55 битов)
2) Определить количество информации, содержащееся в слове из 10 символов, если известно, что мощность алфавита равна 32 символам. (50 бит)
3) Сколько бит информации содержится в сообщении, состоящем из 5 символов, при использовании алфавита, состоящего из 64 символов. (6 битов)
4) Определить информативность сообщения «А + В = С», если для описания математических формул необходимо воспользоваться 64-символьным алфавитом. (30 бит)
5) Для представления числовых данных используют 16-ричный алфавит, включающий знаки математических действий. Сколько битов информации содержит выражение «32 * 5 = 160»? (32 бита)
6) Практическая работа № 2. «Тренировка ввода текстовой и числовой информации с помощью клавиатурного тренажера»
5. Рефлексия.
Источник
Способ измерения информации алфавитный подход
Измерение информации: содержательный и алфавитный подходы. Единицы измерения информации.
Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.
Алфавитный подход к измерению информации.
А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» — «двоичная цифра».
1 бит — это минимальная единица измерения информации!
Один символ алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.
Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.
В любой системе единиц измерения существуют основные единицы и производные от них.
Для измерения больших объемов информации используются следующие производные от байта единицы:
Источник
