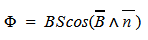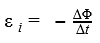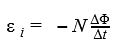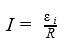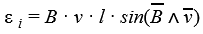- Закон электромагнитной индукции
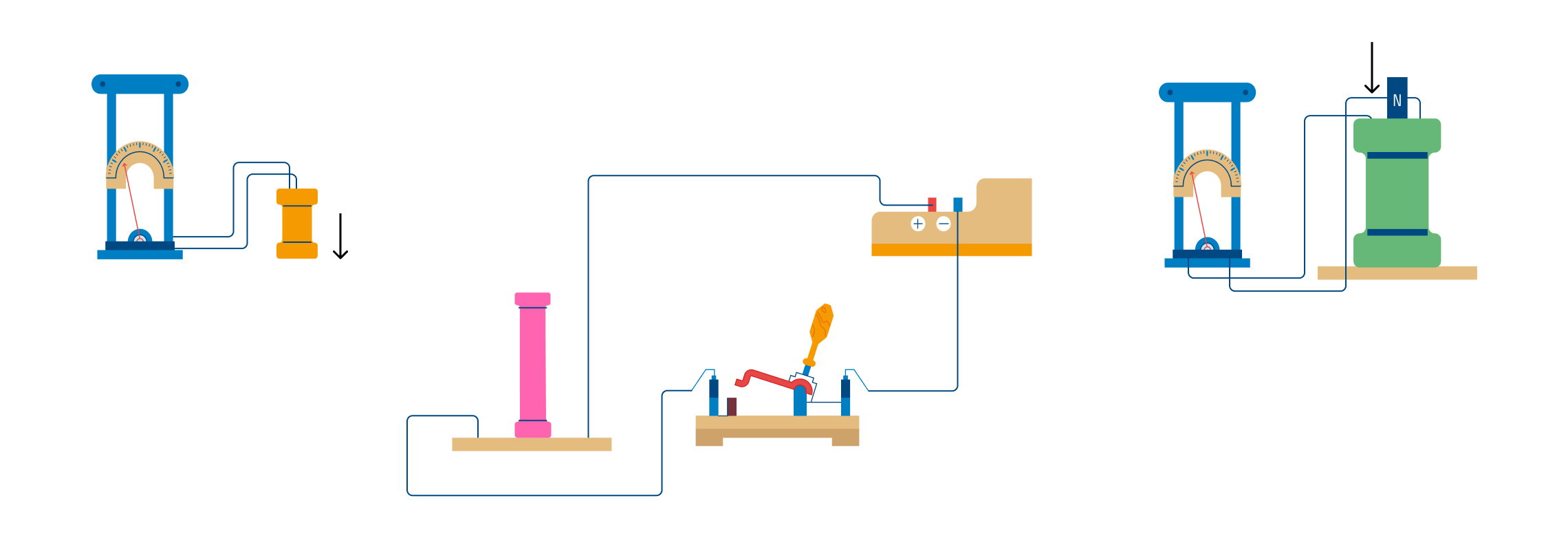
- Магнитный поток
- Электромагнитная индукция
- Закон электромагнитной индукции
- Правило Ленца
- Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках
- Прямое измерение индукции магнитного поля
- Косвенные методы измерение напряженности и индукции магнитного поля
- Измерение напряженности магнитного поля методом Гаусса
- Среднее значение эдс индукции по абсолютной величине меньше абсолютной величины эдс источника тока
- Магнитный поток
- ЭДС в быту и единицы измерения
- Что такое ЭДС индукции
- Законы Фарадея и Ленца
- ТЕМА: ОПРЕДЕЛЕНИЕ ЭДС И ВНУТРЕННЕГО СОПРОТИВЛЕНИЯ ИСТОЧНИКА ТОКА
- Движение провода в магнитном поле
- Вращающаяся катушка
- Труды в области электролиза
- ЭДС самоиндукции
- Простое объяснение электродвижущей силы
- Взаимоиндукция
- Физика
- Где используются разные виды ЭДС
Закон электромагнитной индукции
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
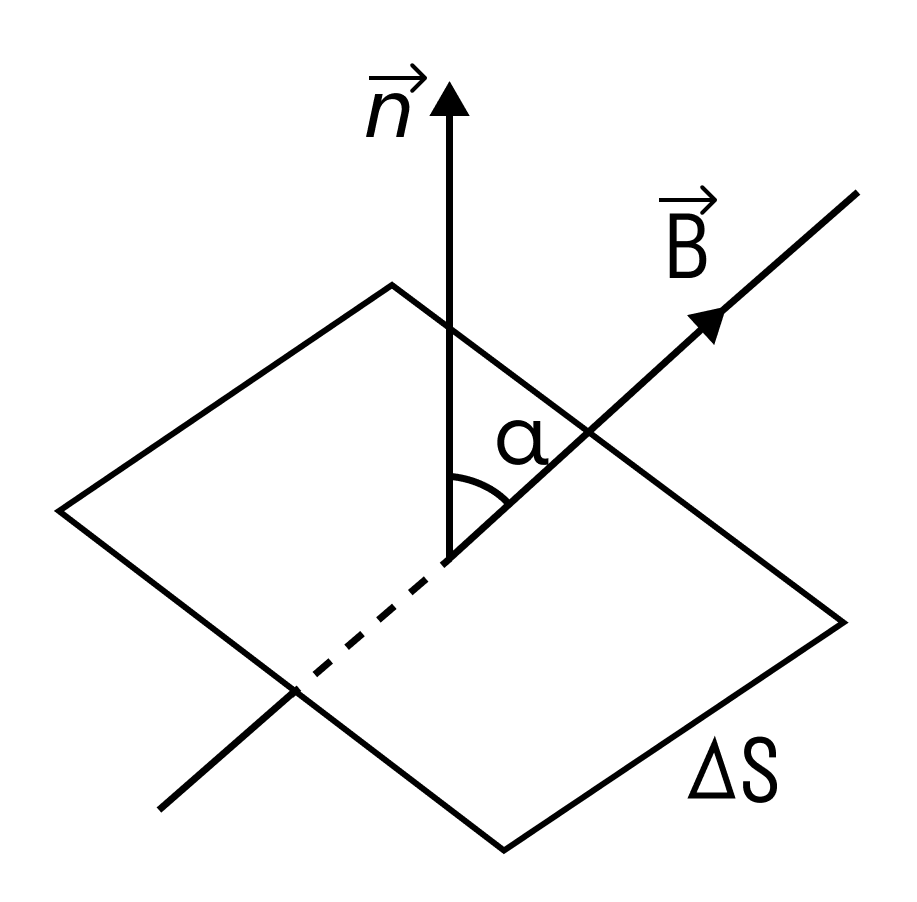
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
| № | Напряжение на внешней части цепи U, В | Сила тока в цепи I,А | Внутреннее сопротивление r, Ом | Среднее значение внутреннего сопротивления rср, Ом | ЭДС e, В | Среднее ЭДС ecр, В |
Таблица 1 – Экспериментальные данные
Обработка результатов измерения
1. Результаты измерений подставить в уравнение 1 и, решая системы уравнений:
определить внутреннее сопротивление источника по формулам:
2.Далее по формулам (2) определить электродвижущую силу источника, поочередно подставляя три значения r.
3.Записать данные в таблицу 1.
4.Посчитать абсолютную и относительную погрешности методом среднего арифметического (Приложение А).
Контрольные вопросы
1. Какова физическая суть электрического сопротивления?
2. Какова роль источника тока в электрической цепи?
3. Каков физический смысл ЭДС? Дать определение вольту.
4. От чего зависит напряжение на зажимах источника тока?
5. Пользуясь результатами произведенных измерений, определить сопротивление внешней цепи.
Отчет по лабораторной работе №__________
студента группы__________________
ФИО_______________________________________________________________
ТЕМА: ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ МОЩНОСТИ ЭЛЕКТРИЧЕСКОГО ТОКА ЛАМПЫ НАКАЛИВАНИЯ ОТ НАПРЯЖЕНИЯ
Цель: освоить метод измерения мощности, потребляемой электроприбором, основанный на измерении силы тока и напряжения; исследовать зависимость мощности, потребляемой лампочкой от напряжения на её зажимах; исследовать зависимость сопротивления проводника от температуры.
Оборудование: электрическая лампа, источник постоянного напряжения и переменного, реостат ползунковый, амперметр; вольтметр, ключ, соединительные провода, миллиметровая бумага.
Краткие теоретические сведения
Величина, равная отношению работы тока А ко времени t, за которое она совершается, называется мощностью P:
Порядок выполнения работы
Эксперимент №1
1.Составить электрическую цепь по схеме, изображенной на рисунке 1, для нулевого опыта соблюдая полярность приборов
Рисунок 1 – Схема подключения
2.Определить цену деления шкалы измерительных приборов
3.После проверки схемы преподавателем, снять показания напряжения U и силы тока I.
4.Данные приборов записать в таблицу 1.
Таблица 1 – Экспериментальные данные №1
| Напряжение на зажимах лампы U, B | Cила тока в лампе I, А | Мощность, потребляемая лампой Р, Вт | Сопротивление нити накала лампы при комнатной температуре Rt, Ом | Сопротивление нити накала лампы для нулевого опыта R0, Ом |
Эксперимент №2.
1.Собрать схему по рис.2, где лампочка через реостат подключается к переменному току.
Рисунок 4.12 – Схема подключения
2.После проверки схемы преподавателем, снять показания амперметра и вольтметра, изменяя положение ползунка на реостате 10 – 11 раз.
3.Данные приборов записать в таблицу 2.
Таблица 2 – Экспериментальные данные №2
| № | Напряжения на зажимах лампы Umax, B | Cила тока в лампе Imax, А | Мощность, потребляемая лампой Р, Вт | Сопротивление нити накала лампы R, Ом | Температура накала Т, оК |
| … |
Обработка результатов измерения
Эксперимент №1
1.Рассчитать значение сопротивления нити накала при комнатной температуре:
2.Найти сопротивление R0
, для нулевого опыта:
где ΔТ0К – изменение абсолютной температуры (в данном случае равна комнатной температуре по шкале Цельсия); α [K-1] – коэффициент температурного сопротивления для вольфрама (Приложение Б).
3.Полученные данные занести в таблицу 1.
Эксперимент №2
1.Для каждого опыта определить мощность Р, потребляемую лампой по формуле:
2.Рассчитать сопротивление нити накала лампы:
3.Найти температуру нити накала лампы для каждого опыта по формуле:
4.Результаты измерений и вычислений занести в таблицу 2.
5.На миллиметровой бумаге построите графики: а) зависимость мощности Р, потребляемой лампой, от напряжения U, на ее зажимах; б) зависимость сопротивления R от температуры Т.
6.Сделайте вывод по результатам двум экспериментов.
Контрольные вопросы
1. Каков физический смысл напряжения на участке электрической цепи?
2. Как определить мощность тока с помощью амперметра и вольтметра?
3. Для каких целей используют ваттметр. Как он включается в цепи?
4. Как изменится сопротивление металлического проводника с увеличением температуры?
5. Чем спираль 100 Вт лампы накаливания отличается от спирали лампы 25 – ваттной?
Движение провода в магнитном поле
Как показано в первой формуле (Е = В * l * v * sinα), амплитуда электродвижущей силы в значительной мере зависит от параметров проводника. Точнее – влияние оказывает количество силовых линий на единицу длины рабочей области цепи. Аналогичный вывод можно сделать с учетом изменения скорости перемещения. Следует не забывать о взаимном расположении отмеченных векторных величин (sinα).
Важно! Перемещение проводника вдоль силовых линий не провоцирует индуцирование электродвижущей силы.
Вращающаяся катушка
Обеспечить оптимальное расположение функциональных компонентов при одновременном перемещении сложно, если применять представленный в примере прямой провод. Однако согнув рамку, можно получить простейший генератор электроэнергии. Максимальный эффект обеспечивает увеличение количества проводников на единицу рабочего объема. Соответствующая отмеченным параметрам конструкция – катушка, типичный элемент современного генератора переменного тока.
Для оценки магнитного потока (F) можно применить формулу:
где S – площадь рассматриваемой рабочей поверхности.

Формулы для расчета и особенности конструкции типичного генератора
Пояснение. При равномерном вращении ротора происходит соответствующее циклическое синусоидальное изменение магнитного потока. Аналогичным образом меняется амплитуда выходного сигнала. Из рисунка понятно, что определенное значение имеет величина зазора между основными функциональными компонентами конструкции.
Труды в области электролиза
При использовании законов Фарадея описываются закономерности, которые существуют при электролизе. Этот процесс заключается в превращении веществ с разнообразными характеристиками. Это происходит при движении электричества сквозь электролит.
Эти закономерности были доказаны М. Фарадеем в 1834 году. Первое утверждение гласит, что масса вещества, которое образуется на электроде, меняется соответственно заряду, перемещенному сквозь электролит.
Второе утверждение гласит, что эквиваленты компонентов с разными характеристиками пропорциональны химическим эквивалентам этих компонентов.
Оба представленных утверждения совмещаются в объединенный закон Фарадея. Из него следует, что число Фарадея будет равняться электричеству, способному выделить на электролите 1 моль вещества. Ее рассчитывают на единицу валентности. Именно по объединенной формуле в далеком 1874 году был вычислен заряд электрона.
Законы электролиза, установленные Фарадеем, тестировались при различном значении тока, температуры, давления, а также при одновременном выделении двух и более веществ. Электролиз также проводился в разных расплавах и растворителях. Концентрация электролита также отличалась в разных опытах. При этом иногда наблюдались небольшие отклонения от закона Фарадея. Они объясняются электронной проводимостью электролитов, которая определяется наравне с ионной проводимостью.
Открытия, сделанные английским физиком М. Фарадеем, позволили описать множество явлений. Его законы являются основой современной электродинамики. По этому принципу функционирует различное современное оборудование.
ЭДС самоиндукции
Если через катушку пропускать переменный ток, рядом будет формироваться электромагнитное поле с аналогичными (равномерно изменяющимися) силовыми характеристиками. Оно создает переменный синусоидальный магнитный поток, который, в свою очередь, провоцирует перемещение зарядов и образование электродвижущей силы. Данный процесс называют самоиндукцией.
С учетом рассмотренных базовых принципов несложно определить, что F = L * l. Значение L (в генри) определяет индуктивные характеристики катушки. Этот параметр зависит от количества витков на единицу длины (l) и площади поперечного сечения проводника.
Простое объяснение электродвижущей силы
Предположим, что в нашей деревне имеется водонапорная башня. Она полностью наполнена водой. Будем думать, что это обычная батарейка. Башня — это батарейка!
Вся вода будет оказывать сильное давление на дно нашей башенки. Но сильным оно будет только тогда, когда это строение полностью наполнено H2O.
В итоге чем меньше воды, тем слабее будет давление и напор струи будет меньше. Открыв кран, заметим, что каждую минуту дальность струи будет сокращаться.
В результате этого:
- Напряжение – это сила с которой вода давит на дно. То есть давление.
- Нулевое напряжение — это дно башни.
С батареей все аналогично.
Первым делом подключаем источник с энергией в цепь. И соответственно замыкаем ее. Например, вставляем батарею в фонарик и включаем его. Изначально заметим, что устройство горит ярко. Через некоторое время его яркость заметно понизится. То есть электродвижущая сила уменьшилась (вытекла если сравнивать с водой в башне).
Если брать в пример водонапорную башню, то ЭДС это насос качающие воду в башню постоянно. И она там никогда не заканчивается.
Взаимоиндукция
Если собрать модуль из двух катушек, в определенных условиях можно наблюдать явление взаимной индукции. Элементарное измерение покажет, что по мере увеличения расстояния между элементами уменьшается магнитный поток. Обратное явление наблюдается по мере уменьшения зазора.
Чтобы находить подходящие компоненты при создании электрических схем, необходимо изучить тематические вычисления:
- можно взять для примера катушки с разным количеством витков (n1 и n2);
- взаимоиндукция (M2) при прохождении по первому контуру токаI1 будет вычислена следующим образом:
- после преобразования этого выражения определяют значение магнитного потока:
- для расчета эдс электромагнитной индукции формула подойдет из описания базовых принципов:
E2 = — n2 * ΔF/ Δt = M 2 * ΔI1/ Δt
При необходимости можно найти по аналогичному алгоритму соотношение для первой катушки:
E1 = — n1 * ΔF/ Δt = M 1 * ΔI2/ Δt.
Следует обратить внимание, что в этом случае значение имеет сила (I2) во втором рабочем контуре.
Совместное влияние (взаимоиндукцию – М) рассчитывают по формуле:
Специальным коэффициентом (K) учитывают действительную силу связи между катушками.
Физика
При изменении потока, сцепленного с замкнутым проводящим контуром, через площадь, ограниченную данным контуром, в нем появляется вихревое электрическое поле и течет индукционный ток — явление электромагнитной самоиндукции.
Модуль средней ЭДС самоиндукции за определенный промежуток времени рассчитывают по формуле
〈 | ℰ i s | 〉 = | Δ Ф s | Δ t ,
где ΔФ s — изменение магнитного потока, сцепленного с контуром, за время Δ t .
Если сила тока в контуре изменяется с течением времени I = I ( t ), то
- изменение потока, сцепленного с контуром, определяется формулой
где L — индуктивность контура; Δ I — изменение силы тока в контуре за время Δ t ;
- модуль средней ЭДС самоиндукции за определенный промежуток времени рассчитывается по формуле
〈 | ℰ i s | 〉 = L | Δ I | Δ t ,
где Δ I /Δ t — скорость изменения силы тока в контуре.
Если индуктивность контура изменяется с течением времени L = L ( t ), то
- изменение потока, сцепленного с контуром, определяется формулой
где Δ L — изменение индуктивности контура за время Δ t ; I — сила тока в контуре;
- модуль средней ЭДС самоиндукции за определенный промежуток времени рассчитывается по формуле
〈 | ℰ i s | 〉 = I | Δ L | Δ t .
Пример 16. В замкнутом проводящем контуре с индуктивностью 20 мГн течет ток силой 1,4 А. Найти среднее значение ЭДС самоиндукции, возникающей в контуре, при равномерном уменьшении в нем силы тока на 20 % за 80 мс.
Решение . Появление ЭДС самоиндукции в контуре вызвано изменением потока, сцепленного с контуром, при изменении в нем силы тока.
Поток, сцепленный с контуром, определяется формулами:
где L — индуктивность контура, L = 20 мГн; I 1 — первоначальная сила тока в контуре, I 1 = 1,4 А;
где I 2 — конечная сила тока в контуре.
Изменение потока, сцепленного с контуром, определяется разностью:
Δ Ф s = Ф s 2 − Ф s 1 = L I 2 − L I 1 = L ( I 2 − I 1 ) ,
где I 2 = 0,8 I 1 .
Среднее значение ЭДС самоиндукции, возникающей в контуре, при изменении в нем силы тока:
〈 ℰ s i 〉 = | Δ Ф s Δ t | = | L ( I 2 − I 1 ) Δ t | = | − 0,2 L I 1 Δ t | = 0,2 L I 1 Δ t ,
где ∆ t — интервал времени, за который происходит уменьшение силы тока, ∆ t = 80 мс.
Расчет дает значение:
〈 ℰ s i 〉 = 0,2 ⋅ 20 ⋅ 10 − 3 ⋅ 1,4 80 ⋅ 10 − 3 = 70 ⋅ 10 − 3 с = 70 мВ.
При изменении силы тока в контуре в нем возникает ЭДС самоиндукции, среднее значение которой равно 70 мВ.
Где используются разные виды ЭДС
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.

Принцип действия трансформатора
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Источник