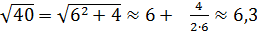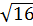Таблица квадратов чисел до 100 за неделю. Как выучить квадраты чисел без зубрежки за неделю
Книга является продолжением методики, использованной в книге «Таблица умножения за 3 дня». Методики, в которой результат получается методом лёгких вычислений без «зубрёжки» (аналогично тому, как получается результат умножения на 10, путём приписывания цифры 0 к умножаемому). Вычисления доступны ученикам 3-го класса (знают таблицу умножения и умеют делать арифметические действия).
Оглавление
Приведённый ознакомительный фрагмент книги Таблица квадратов чисел до 100 за неделю. Как выучить квадраты чисел без зубрежки за неделю предоставлен нашим книжным партнёром — компанией ЛитРес.
Формула квадратов чисел от 11 до 19
Данная формула применима для вычисления квадратов, как частного случая умножения чисел от 11 до 19, когда оба числа одинаковые.
Детям младших классов (3—5 класс) формулу объясняю как методику.
Обозначим цифры единиц чисел из интервала [11, 19] как Х и У. Тот факт, что число десятков равно 1, учтём в формуле как 1 в нужном разряде. Нижним подчёркиванием (вместо математического верхнего) покажем, что умножаются числа 1Х и 1У. Тогда вся формула будет иметь вид:
Формула умножения, чисел из отрезка [11, 19]
Словами можно объяснить так:
Приумножении чисел из промежутка [11, 19] нужно поступить таким образом. К первому числу надо добавить единицы второго числа (можно наоборот ко второму числу прибавить единицы первого числа). Полученный результат умножить на 10 (приписать справа 0) и прибавить произведение единиц первого и второго числа.
Так как данная книга о квадратах чисел, то применим данную формулу к частным случаям (когда Х=У):
11 2 =11*11= (11+1) *10+1*1=120+1=121;
12 2 =140+2 2 =144;
13 2 =160+3 2 =169;
14 2 =180+4 2 =196;
15 2 =200+5 2 =225;
16 2 =220+6 2 =256;
17 2 =240+7 2 =289;
Необходимо добиться навыка подсчета таких чисел, как в последних двух примерах (18 и 19), когда многие промежуточные выкладки сведены к сумме двух слагаемых. Вполне можно добиться навыка простого запоминания этих квадратов. Подробнее о технике запоминания будет изложено в другом разделе книги, касающегося мнемотехники.
Доказать справедливость формулы подсчёта таких чисел можно алгебраическими методами.
Перепишем числа 1Х и 1У как 10+Х и 10+У, где Х и У это единицы первого и второго числа.
Тогда (10+Х) * (10+У) =100+10Х+10У+Х*У= (10+Х+У) *10+Х*У.
Выражение в скобках (10+Х+У) это сумма первого числа 10+Х с единицами У второго числа или сумма второго числа 10+У с единицами Х первого числа. Далее полученный результат умножается на 10 и суммируется с произведением единиц первого и второго чисел. Данное правило и было описано словесно в этой главе.
Формула квадратов для чисел, оканчивающихся на 5
Эта формула распространяется и на другие случаи умножения двузначных чисел с одинаковым числом десятков и когда сумма единиц равна 10. Один из частных случаев этой формулы применяется для вычисления квадратных корней для чисел, оканчивающихся на 5.
В этой главе приведу частный случай этой формулы. О самой формуле напишу более подробно в другой моей книге.
Формула вычисления квадратов, для чисел, оканчивающихся на 5:
Квадраты чисел, оканчивающихся на 5
По сути, если число заканчивается на 5, то нужно число десятков увеличить на 1 и перемножить эти числа, в конце полученного результата дописать 25.
1) 15 2 =1* (1+1) *100+5 2 =200+25=225;
2) 25 2 =2* (2+1) *100+5 2 =600+25=625;
3) 75 2 =7*8*100+5 2 =5600+25=5625;
5) 115 2 =11*12*100+25=13225
На практике никакого умножения на 100 не производится. На самом деле сначала пишут результат умножения числа десятков на следующее за ним число и к нему приписывается 25:
Представим число оканчивающееся на 5 как 10*Х+5, где Х-любое число из натурального ряда (5 пример показывает, что число может быть любым, а не только однозначным).
Х5 2 = (10Х+5) * (10Х+5) =100Х 2 +50Х+50Х+5*5=100Х 2 +100Х+25=100Х* (Х+1) +25=Х* (Х+1) *100+25=Х* (Х+1) 25
Формула квадратов чисел от 25 до 50
Многие вычислители (ментальные счётчики, фокусники-математики) используют следующую формулу для вычисления чисел из отрезка [25;50].
Источник
Глава 2. Способ с применением таблицы квадратов
Двузначных чисел
С этим способом мы познакомились на уроках математики. Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора. Но для этого метода требуется наличие таблицы квадратов натуральных чисел от 10 до 99. (Она есть во всех учебниках алгебры 8 класса, и на экзамене ГИА предлагается в качестве справочного материала).
Откройте таблицу и проверьте скорость нахождения ответа. Но при использовании таблицы квадратов для извлечения квадратного корня нужно не перепутать, что крайний левый столбик определяет цифру, стоящую в разряде целых, а самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее 100 подкоренное число, и далее действуйте по правилам этой таблицы.
Пример 1: Найдём значение 
Решение: Мысленно отбрасываем две последние цифры у всех чисел в таблице и находим 57 или близкие к 57-ти – такое число одно 5776. Левый столбик даёт ответ 7 (это целые), а верхняя строчка 6 (это десятые). Значит 

Пример 2: Найдём значение 
Решение: Мысленно поставим запятые, отсчитав две последние цифры, у всех чисел в таблице и находим близкие для 89 – таких только два 88,36 и 90,25. Но 90,25 – это много, 88,36 ближе к 89. Значит, выбираем 8836.
Левый столбик даёт ответ 9 (это целые), а верхняя строчка 4 (это десятые). Значит 

Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 мы уже этим способом извлечь не сможем. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Глава 3. Формула Древнего Вавилона
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа n.
Число n они представляли в виде суммы а 2 + b, где а 2 ближайший к числу n точный квадрат натурального числа а и пользовались формулой:
Извлечём с помощью этой древней формулы корень квадратный из числа 40:
| Результат извлечения корня из 40 с помощью микрокалькулятора равен 6,324555. Как видим, способ вавилонян дает хорошее приближение к точному значению корня. Но без знания полных квадратов больших чисел и умения их быстро находить, результат извлечения будет найти крайне затруднительно. |
Глава 4. Через решение уравнения
На самом деле существует удобный способ нахождения квадратного корня «вручную» через решение уравнения, ведь математика — наука с многовековой историей, а калькуляторы были не всегда. Способ этот дает возможность вычислить значение корня с точностью до одного — двух знаков после запятой, а, при желании, достичь и большей точности. Звучит невероятно, но попробуйте испытать этот способ при вычислении квадратного корня.
Суть этого способа рассмотрим на примере и попробуем вычислить значение 
Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 16 = 4² и 25 = 5²,
поэтому
следовательно 
Возведем в квадрат обе части полученного уравнения и раскроем скобки при помощи формулы суммы квадрата:
( 
Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х²явно достаточно малая дробь, то ей вполне можно пренебречь.
В результате приходим к простому линейному уравнению
Решив его, получаем значение х = 0,5.
Значит 
На самом деле, при расчете на калькуляторе, значение этого корня равно 4,47213595, то есть погрешность при нашем расчете составила 0,02786405. Не правда ли, вполне приличная точность!
Но если все же решение задач по математикетребует еще большей точности, то можно достичь ее тем же способом, просто продолжив вычисления с уже полученным значением корня. Так что подобный способ вычисления квадратного корня необычайно точен и удобен, а погрешность вычисления зависит исключительно от вашего терпения и упорства.
Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.
Дата добавления: 2019-01-14 ; просмотров: 301 ; Мы поможем в написании вашей работы!
Источник
Быстрое возведение чисел от 1 до 100 в квадрат
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
Достаточно трудно, верно? Давайте разберем пример:
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
Тоже достаточно трудно для восприятия. Давайте разберем пример:
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
Для чисел от 50 до 100
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»: 
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Источник