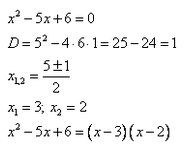- Метод интервалов, решение неравенств
- Определение квадратного неравенства
- Решение неравенства графическим методом
- Решение неравенства методом интервалов
- Плюс или минус: как определить знаки
- Презентация + урок по математике для 9 класса «Метод интервалов»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Метод интервалов, решение неравенств
О чем эта статья:
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
- D
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком
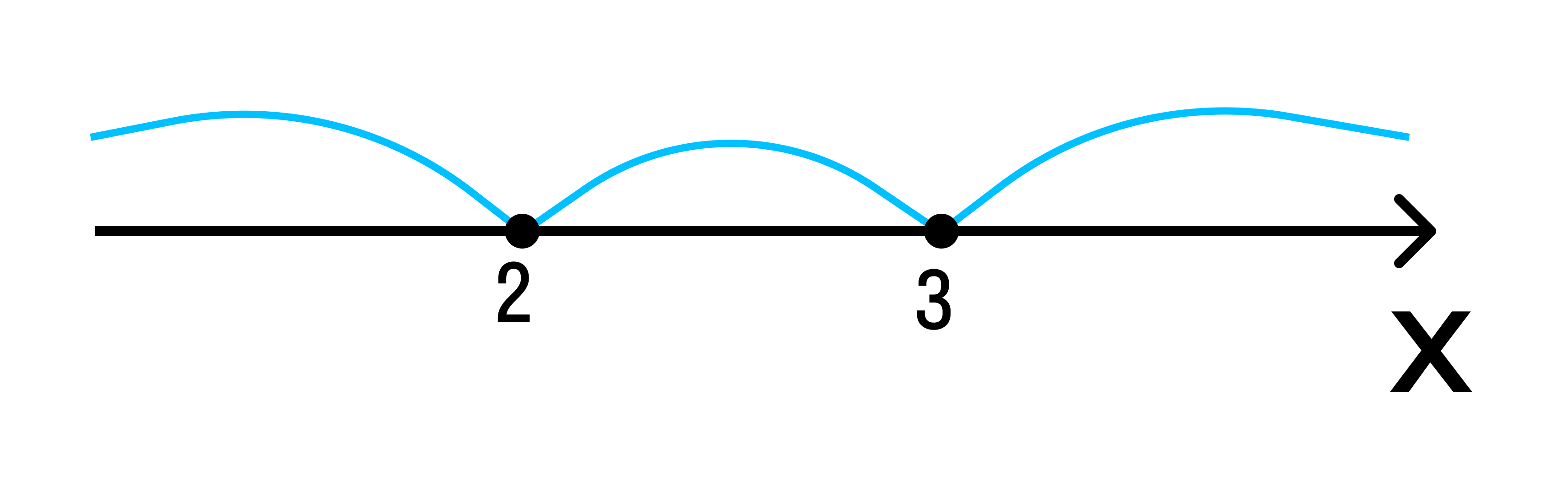
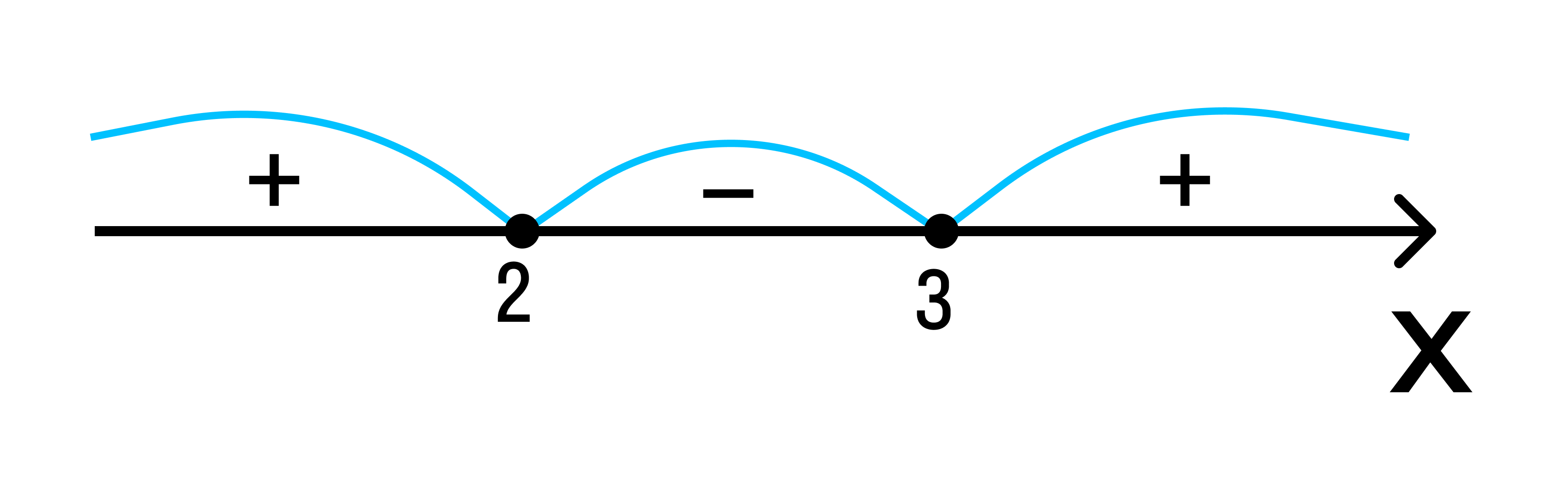
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Источник
Презентация + урок по математике для 9 класса «Метод интервалов»
Выбранный для просмотра документ Решение неравенств методом интервалов урок1.pptx
Описание презентации по отдельным слайдам:
МБОУ ”Междуреченская СОШ №6” Решение неравенств методом интервалов 9 класс урок 1 Учитель: О.Г.Худякова п.Междуреченский 2013 год
Нам надо решить вот такое неравенство: (x − 5)(x + 3) > 0 Какие есть варианты?
Во-первых:правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 4 слайд 
Во-вторых: слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем: x2 − 2x − 15 > 0 Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0.
Попробуем нарисовать схему этой параболы: Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Почему эти методы неэффективны? Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
А теперь представьте, что множителей будет не 2, а хотя бы 4. Например: (x − 7)(x − 1)(x + 4)(x + 9) 9 слайд 
Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости. Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов? Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) 11 слайд 
Алгоритм состоит из 4 шагов: Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще; Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов; Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней; Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) 12 слайд 
Решите неравенство: (x − 2)(x + 7) 13 слайд 
Шаг 2: отмечаем эти корни на координатной прямой. Имеем:
Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 Получим: f (x) = (x − 2)(x + 7); f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10; Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Шаг 4: надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс, поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс
Осталось отметить эти знаки на координатной оси. Имеем: Вернемся к исходному неравенству, которое имело вид: (x − 2)(x + 7) 17 слайд 
Замечания по поводу знаков функции Наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен: Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374. Почему это важно? Все точки на одном интервале дают один и тот же знак. Помните об этом!
Практическая работа Решите неравенства: (x + 9)(x − 3)(1 − x) 21 слайд 
(x − 1)(2 + x)(7 − x) 22 слайд 0 Ответ: x ∈ (−4; 0) ∪ (3; +∞) В классе: № 325 Д/з: № 326. » title=»x(2x + 8)(x − 3) > 0 Ответ: x ∈ (−4; 0) ∪ (3; +∞) В классе: № 325 Д/з: № 326. «> 
x(2x + 8)(x − 3) > 0 Ответ: x ∈ (−4; 0) ∪ (3; +∞) В классе: № 325 Д/з: № 326(а,г — ”3”, весь №- “4,5”)
Итог урока продолжи Я узнал на уроке… Я научился… Я умею… Спасибо за работу!
Выбранный для просмотра документ прил к уроку1.doc
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 812 человек из 76 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 286 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 599 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
«Описание материала:
Предлагаю Вам разработку урока №1 в теме “Метод интервалов” в курсе «алгебры 9 класса.
Данная разработка представляет презентацию к уроку + приложения. Приложение представлено в виде алгоритма решения неравенств методом интервалов.
В начале урока предлагается решение неравенств известными способами. Затем рассматривается неэффективность данных способов.
Через презентацию ученики подводятся к цели урока и способам решения неравенств вида (х-х1)(х-х2)0.
Далее на закрепление предлагается решение неравенств с помощью данного метода. урок относится к преподаванию математики, презентации.
Номер материала: 25990011511
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ
Время чтения: 1 минута
Шойгу предложил включить географию в число вступительных экзаменов в вузы
Время чтения: 1 минута
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Российский совет олимпиад школьников намерен усилить требования к олимпиадам
Время чтения: 2 минуты
Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник