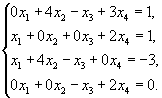Способ их решения задач по высший математики

Примеры решений задач по высшей математике

На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.

Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.

Далее решенные задачи по темам:

Высшая математика. Комплексные числа

Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.

Высшая математика. Матрицы

Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.

$$A= \begin 1 & 2 & 1 & -1\\ 1 & 1 & 0 & 0\\ 0 & 2 & 0 & -1\\ 1 & 1 & 1 & 0\\ \end $$

Высшая математика. Определители

Задача. Вычислить определитель матрицы $A$

$$A= \begin 4 & 5 & 6 & 5 & 11\\ 1 & 4 & 2 & 0 & 13\\ 1 & 1 & 0 & -1 & 5\\ 3 & 2 & 3 & 0 & 7\\ 4 & 1 & 2 & 3 & 8\\ \end $$

Высшая математика. Системы уравнений

Задача. Исследовать на совместность и решить систему уравнений:

Высшая математика. Векторы

Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.

Аналитическая геометрия на плоскости

Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $\cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Аналитическая геометрия в пространстве

Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Высшая математика. Пределы

Задача. Найти предел функции

Высшая математика. Производные

Задача. Найти производную от следующей функции

Высшая математика. Исследование функции

Задача. Провести полное исследование функции и построить график.

Высшая математика. Интегралы

Высшая математика. Применение интегралов

Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:

$$ x=3(1-\cos t)\cos t, \quad y=3(1-\cos t)\sin t, \quad 0\leq t \leq \pi. $$

Высшая математика. Кратные и криволинейные интегралы

Высшая математика. Ряды

Задача. Исследовать сходимость числового ряда

Высшая математика. Дифференциальные уравнения

Задача. Найти общее решение линейного дифференциального уравнения первого порядка

Высшая математика. Теория вероятностей

Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.

Источник

Лекции и уроки по высшей математике

Карта сайта mathprofi.ru

Спокойно-спокойно – не удивляемся, такой «небоскрёб» «возведён» для удобства мобильных пользователей. Приветствую тех, кто зашёл на эту страничку с поисковика, меня зовут Емелин Александр и я рад представить вам свой курс высшей математики. Лекции и уроки носят практическую направленность и, кроме того, позволяют разобраться в теории. Поехали:

Если Вы хотите найти что-то конкретное, то имеет смысл сразу же воспользоваться поиском по сайту:

Поиск >>>

Не нашлось нужного материала?

Зайдите на страницу с тематическими архивами или посетите нашу библиотеку mathprofi.com, в которой можно раздобыть методички, лекции, контрольные, и др. учебные материалы.

Совсем-совсем дела плохи? Задайте вопрос на форуме!

Есть вопрос лично ко мне? Посмотрите часто задаваемые вопросы и если что – обращайтесь! Оставить свой отзыв можно в гостевой книге.

Для людей, начинающих изучать высшую математику, а также желающих восстановить свои знания/навыки предназначена организационная статья, которая так и называется:

Рекомендуемые математические ресурсы здесь >>>

Список доходчивой литературы здесь >>>

«Кладовка» со справочными материалами – здесь.

Кликаем по интересующему разделу и «спускаемся на лифте» к его подробному описанию! Все статьи в той или иной теме (и сами темы) я старался расположить в логической последовательности их изучения:

Аналитическая геометрия

Высшая алгебра

Пределы

Производная и некоторые её приложения

Функции и графики

Функции нескольких переменных

Однократные интегралы

Дифференциальные уравнения

Числовые ряды

Функциональные ряды

Кратные, криволинейные и поверхностные интегралы

Элементы векторного анализа

Комплексный анализ

Теория вероятностей

Я не хочу оформлять карту сайта «штабелем ссылок» и составляю её вручную, поэтому в настоящий момент здесь могут быть представлены не все темы. В том случае, если Вы не видите нужных разделов, пользуйтесь Поиском либо ориентируйтесь по левому навигационному меню, например, главной страницы

Аналитическая геометрия

В данном разделе можно выделить несколько блоков:

Векторы. «Альфа» и «омега» аналитической геометрии. Начинаем с двух базовых уроков:

и продолжаем следующими статьями:

Здесь наиболее трудной является 2-я лекция (о переходе) и поэтому я не рекомендую спешить с её изучением

Прямая на плоскости представлена следующими страницами:

Уравнение прямой на плоскости
Основные задачи с прямой на плоскости
Линейные неравенства
и Задача с треугольником, где я разбираю не только её, но вручаю вам «ключ» к решению многих задач по теме, да и не только по этой теме.

Линии второго порядка. Данный цикл лекций-уроков примечателен тем, что в него удалось ненавязчиво вместить значительное количество теории:

Полярная система координат. С ней целесообразно ознакомиться после изучения предыдущей темы, ибо окружностей и иже с ними тут хватает:

Полярные координаты – теоретические азы и простейшие примеры;
Практикум по построению типовых кривых в ПСК

И, наконец, геометрия пространства, где, наоборот – ярко выражена практика:

Высшая алгебра

Данный раздел также делится на несколько подразделов:

Вводные лекции, которые имеют огромное значение для изучения ВСЕГО курса высшей математики:

Комплексные числа. Любимая многими тема!

Комплексные числа для «чайников» – понятие и действия с числами;
Выражения уравнения и системы с комплексными числами – добротный и насыщенный практикум по теме.

Матрицы и определители. Уроки для «самых маленьких»:

и более серьёзные практические занятия:

Системы линейных алгебраических уравнений.

Опять же – базовый уровень:

Линейные преобразования. Собственно:

Линейные преобразования – интереснейшая и одна из самых важных лекций по алгебре, на которой я рассмотрел не только основы темы, но и обобщил понятие вектора.
Собственные числа и собственные векторы – наиболее известная и популярная задача.

Квадратичные формы. Держат нас в форме!

Понятие квадратичной формы, обычная и матричная запись, а также знакоопределенность и критерий Сильвестра;
Приведение формы к каноническому виду. Метод Лагранжа
Ортогональное преобразование квадратичной формы и геометрическое приложение – приведение уравнения линии 2 порядка данным методом.

Пределы

Пределы без предела =)

Базовые уроки для прожжённых гуманитариев:

и тотальный «разгром» лимитов для угорелых технарей:

+ более чем доступная лекция по теории, открывающая дверь в удивительный мир математического анализа:

Производная и некоторые её приложения

Как обычно – «песочница»:

и несколько уроков для отработки техники дифференцирования:

После чего целесообразно ознакомиться с теоретической лекцией Что такое производная? и потренироваться в нахождении производной по определению (нужно уметь находить пределы – см. выше)

И заключительная порция статей посвящена некоторым приложениям производной:

Уравнение нормали
Приближённые вычисления с помощью дифференциала (здесь волею судьбы оказалось рассмотрена и аналогичная задача для функции двух переменных)
Метод касательных

Функции и графики

Две справочно-прикладные статьи, без которых никуда! Причём во всей вышке:

Основной же цикл статей посвящён исследованию функции:

По материалам перечисленных уроков создан удобный справочный конспект:
Схема исследования функции

+ Нахождение наибольшего и наименьшего значений функции на отрезке
(самостоятельная задача и иногда «довесок» к полному исследованию)

Функции нескольких переменных

Один из предметов моей гордости – пожалуй, наиболее трудный в создании раздел. Его можно условно разделить на две части:

Область определения и линии уровня функции двух переменных – intro;
Основные поверхности пространства – не только справочная статья, но и ценное руководство по технике ручного построения поверхностей.

+ три «ласточки» на пределы и непрерывность:

Вторая часть раздела касается дифференцирования ФНП. Сначала отрабатываем технику решения:

после чего окончательно разбираемся в сути частных производных:

Производная по направлению и градиент – отличная лекция, не пропустите!

И наиболее распространённые приложения:

Однократные интегралы

В этот обширный раздел включены лекции-уроки о неопределенных, определённых и несобственных интегралах.

Неопределенные интегралы. Осваиваем «интегральный минимум студента»:

и укрепляемся на завоёванных рубежах:

Определённые интегралы. Тактика та же – изучаем вводную статью по теме + два «заштатных», но очень важных приложения:

Примерно здесь находится Рубикон раздела – знакомимся с лекцией, в которой я раскрыл суть интегрирования:

Несобственные интегралы представлены статьёй:

мануалом для более подготовленных читателей:

и темой для готовеньких:)

На следующих уроках закрепляем навыки решения интегралов:

И ставшие уже традиционными, статьи по численным методам. Как вычислить определённый интеграл приближённо:

Дифференциальные уравнения

Один из самых увлекательных и любимых мной разделов! Чего и вам желаю:

Сначала осваиваем основы темы и ДУ первого порядка.
Как повелось, «скорая помощь»:

а также незаменимый урок о линейных ДУ первого порядка.

И менее распространённые, но не менее важные:

После чего можно перейти к изучению следующего подраздела:

ДУ второго и высших порядков. Эти уравнения делятся на две «ветви»:

И на десерт:

Числовые ряды

Одна из самых простых и прозрачных тем:

Числовые ряды для «чайников» – понятие числового ряда и его сходимости, необходимый признак сходимости ряда, признаки сравнения;
Нахождение суммы ряда
Признак Даламбера, радикальный и интегральный признаки Коши
Знакочередующиеся ряды и признак Лейбница
+ Числовые ряды повышенной сложности – классифицированы!

Функциональные ряды

Для изучения этого раздела нужно освоить числовые ряды (см. выше).

Две статьи для «чайников»:

И отдельная глава:

Ряды Фурье – в конце лекции есть много дополнительных материалов!

Кратные, криволинейные и поверхностные интегралы

Распространение идеи интегрирования на дву- и трёхмерные области.

Уроки по двойным интегралам:

Уроки по тройным интегралам:

Следующую тему изучаем не поверхностно:

А эту – не криво:)

Элементы векторного анализа

Захватывающая, но достаточно трудная тема, требующая знания, в частности криволинейных и поверхностных интегралов:

Основы теории поля – понятие скалярного и векторного поля, векторные линии, градиентное поле, ротор векторного поля, потенциальное поле;
Поток векторного поля, в том числе через замкнутую поверхность;
Дивергенция векторного поля и формула Гаусса-Остроградского
Циркуляция векторного поля и формула Стокса

Комплексный анализ

Статей пока немного, но они в тельняшках:

Рабочий справочный материал по двум нижеследующим статьям:
Таблица оригиналов и изображений

Теория вероятностей

Данную тему можно разделить на две большие главы

Случайные события

Случайные величины (СВ)

Здесь можно выделить три блока.

Дискретные случайные величины:

Непрерывные случайные величины:

Система случайных величин (двумерная случайная величина):

И будьте уверены:

(переход на главную страницу сайта)

Источник