Способ группировки квадратных уравнений

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

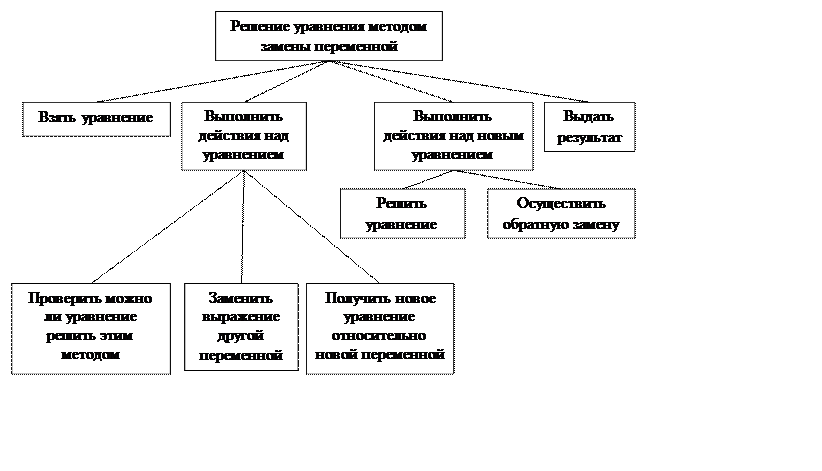
Решение уравнения методами группировки и замены переменной

Страницы работы

Содержание работы

Лабораторная работа №1

Цель работы: Решить уравнения методами:

б) замены переменной.

Теоретическая часть работы

Способ группировки разложение на множители

Для того, чтобы разложить многочлен 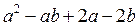на множители:

1 – Объединим слагаемые попарно в группы (говорят «сгруппируем слагаемые»): два в одну группу, и два — в другую .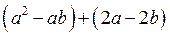

2 – В каждой паре вынесем за скобки общий множитель.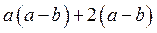

3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки .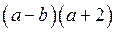

Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.

Рассмотрим решение уравнения способом разложения на множители на конкретном примере:

Применив способ группировки, получим:

Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:

Метод введения новой переменной

Пример.

.

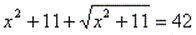
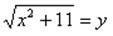
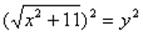
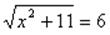
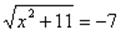
Введем новую переменную , учитывая, что , получаем квадратное уравнение у 2 +у – 42=0 , корни которого -7 и 6. Возвращаясь к переменной х, получаем уравнения и , последнее не имеет корней, т.к. арифметический квадратный корень – неотрицательное число, а первое уравнение можно решить, используя определение арифметического квадратного корня 6 2 = х 2 +11 , решение которого х=5 и х=-5.

Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.

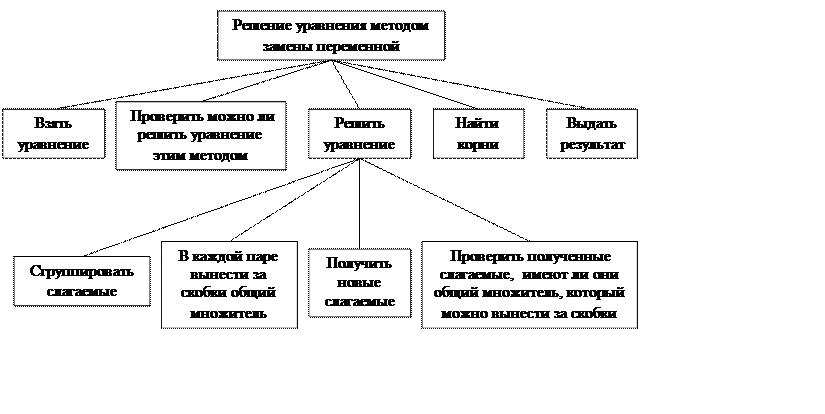
Структурная схема программы: а) способ группировки разложение на множители

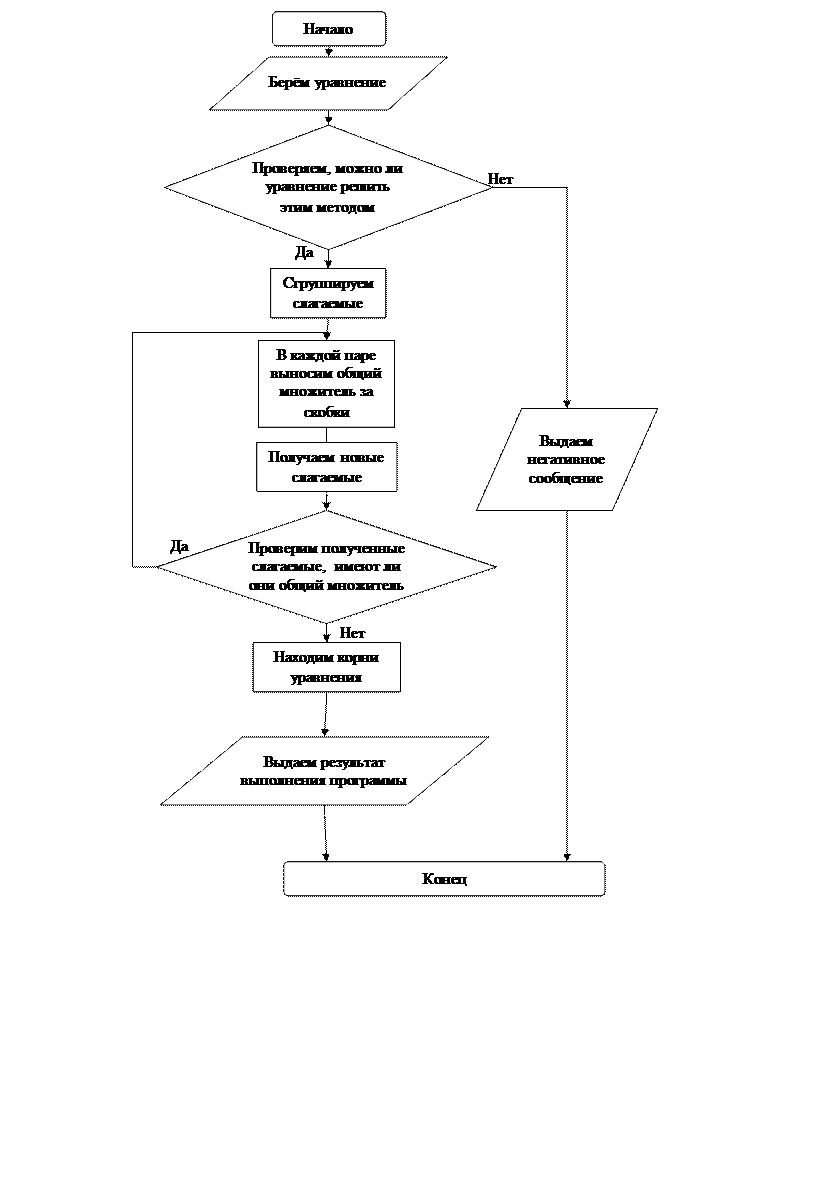
Блок-схема программы: а) способ группировки разложение на множители

Структурная схема программы: б) замены переменной

Блок-схема программы: б) замены переменной

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник

«Нестандартные приемы решений квадратных уравнений»

Урок-конференция по математике для 8 класса

«Нестандартные приемы решений квадратных уравнений».

Учитель математики высшей категории

БОУ «Лицей № 102» г. Железногорск, Красноярский край

Скакунова Людмила Александровна

Материалы урока — конференции «Нестандартные приемы решений квадратных уравнений» соответствуют программным требованиям. В процессе подготовки и проведения этого урока реализуются основные виды УУД:

ориентация в системе знаний по заявленной теме;

постановка учебной задачи, анализ, синтез;

умение работать с информацией;

преобразовывать информацию из одной формы в другую: составлять ответы на вопросы; доказательства своих суждений;

умение формулировать проблему и находить способы её решения.

умение определять и формулировать цель;

планировать своё действие в соответствии с поставленной задачей;

вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.

умение слушать и понимать речь других;

оформлять свои мысли в устной форме;

договариваться с одноклассниками совместно с учителем о правилах поведения и общения и следовать им.

Класс разбивается на группы (по числу докладов). Каждая группа работает над одной из предложенных тем. На уроке осуществляется представление и обсуждение каждого проекта.

Урок-конференция по теме

«Нестандартные приемы решений квадратных уравнений»

Л. А. Скакунова (Железногорск)

Подготовка к конференции

Класс (из 25 человек) разбивается на 5 групп (по числу докладов). Каждая группа работает над одной из предложенных тем по рекомендованной литерату­ре. Через две недели каждая группа в индивидуаль­ной беседе с учителем предлагает варианты изложе­ния темы, определяет докладчика (ученика, лучше других разобравшегося в материале) и его внутренне­го оппонента. Еще через неделю готовый доклад за­слушивается внутри группы, все ее члены знакомятся с содержанием и оформлением доклада (к выступ­лению докладчик готовит компьютерную презен­тацию).

Оборудование и материалы к уроку

Приборы и инструменты для выполнения чертежей и рисунков, компьютер, видеопроектор.

Стенды с материалами по теме конференции.

• Памятки для учащихся с алгоритмами различ­ных способов решения квадратных уравнений; вопросник для оппонентов; оценочный лист.

Основные этапы урока

Этап I . Организационный момент.

Этап II . Вступительное слово учителя.

Приветствие присутствующих, представление участников, сообщение о плане проведения конфе­ренции и порядке выступлений.

Этап III . Сообщения учащихся, выступления оп­понентов. Оценивание выступлений докладчиков.

Укажем перечень тем сообщений.

• Общие методы решения квадратных уравнений.

1. Метод разложения на множители.

2. Методом введения новой переменной.

• Специальные методы решения квадратных уравнений.

1. Использование свойства коэффициентов квад­ратного уравнения.

2. Метод «переброски» старшего коэффициента.

• Графический способ решения квадратных урав­нений.

• Геометрический способ решения квадратных уравнений.

• Способы решения квадратных уравнений в древности

После каждого сообщения заслушивается мнение оппонента. Приведем примерный план выступления оппонента (оценки доклада).

так, что вызывает интерес к теме; от простого к сложному; четко и ясно (или непоследовательно, неуверенно) и т.д.

В выступлении привлекались.

(Указываются средства привлечения внимания учащихся к излагаемому материалу.)

образная; математически грамотная; логически выдержан­ная и т.д.

интересное; новое для меня; может пригодиться в даль­нейшем; вызывает желание продолжить изучение вопроса, по­читать литературу по этой теме и т.д.

У меня следующий вопрос к выступающему. (Формулируется вопрос.)

Мои пожелания выступающему. (Высказываются пожелания.)

Далее каждый ученик класса заполняет полученный в начале урока оценочный лист и сдает его экспертной группе (в составе трех учеников старших классов).

В выступлении докладчика оцениваются (в баллах): знание содержания темы, решение примеров, а также презентация доклада.

0 – 4 балла: тема не раскрыта, допущены фактические и вычислительные ошибки, представление доклада не вызвало интереса к затронутому в нем вопросу;

5 – 7 баллов: тема раскрыта частично, встречались недочеты в решениях примеров, представление докладов в целом понравилось;

8 – 10 баллов: тема раскрыта полностью, не было допущено фактических и вычислительных ошибок, представление доклада вызвало интерес к рассматриваемому вопросу.

Экспертная группа обрабатывает результаты – суммирует выставленные учениками баллы и находит их среднее арифметическое. Кроме того, каждый член экспертной группы заполняет оценочный лист на оппонента (с последующей обработкой результатов – нахождением среднего арифметического баллов)

0 – 4 балла: представлен краткий комментарий, вопросы не задавались;

5 – 7 баллов: представлен подробный комментарий, вопросы не задавались;

8 – 10 баллов: представлен подробный комментарий, задавались вопросы по существу.

Все результаты заносятся в таблицу (используется компьютер).

Этап IV . Домашнее задание.

Задание состоит из подборки уравнений, предло­женных на уроке учениками, делавшими сообщения.

Этап V . Заключительное слово учителя.

После всех выступлений учитель дает оценку предварительной работе учащихся по подготовке к конференции (работе с дополнительной литературой по математике, подготовке презентаций и т.д.), а также прозвучавшим выступлениям; привлекает внимание к материалам стенда; сообщает о возмож­ности продолжить начатую работу.

Этап VI . Подведение итогов урока, выставление оценок докладчикам и лучшим оппонентам.

Тема 1. Общие методы решения квадратных уравнений

При решении квадратных уравнений часто при­меняется метод разложения на множители (с по­мощью вынесения за скобки общего множителя, фор­мул сокращенного умножения или способа группи­ровки).

Пример 1. Решите уравнение

Решение. Воспользуемся способом группировки.

3х² + 3х – х – 1 = 0,

3х(х + 1) – (х + 1) = 0,

х + 1 = 0 или 3х – 1 = 0,

х = -1 х = .

Ответ: -1; .

При решении более сложных квадратных уравнений нередко приходится использовать метод введения новой переменной. Удачный выбор новой переменной делает структуру уравнения более прозрачной и позволяет свести решение к более простому случаю.

Пример 2. Решите уравнение

.

Решение. Пусть t = 5х + 3. Произведем замену переменной:

Убеждаемся, что D > 0. По теореме, обратной теореме Виета, подбираем корни: t ₁ = 1, t ₂ = 2.

Произведем обратную замену и вернемся к переменной х.

Если t = 1, то Если t = 2, то

Замечание. При решении квадратного уравнения не следует торопиться выполнять преобразования. Сначала надо посмотреть, нельзя ли записать уравнение проще, введя новую переменную.

Задание на дом. Решите уравнения, используя метод разложения на множители или введение новой переменной.

х 2 + 16х + 15 = 0; (3х + 2)² = 4 + 12х.

Тема 2. Специальные методы решения квадратных уравнений

Рассмотрим решение квадратных уравнений, коэффициенты которых обладают определенными свойствами. Установим связь между суммой коэффициентов уравнения и его конями.

1) х² +4х – 5 = 0, 2) х² + 6х + 5 = 0,

a = 1, b = 4, c = — 5, a = 1, b = 6, c = 5,

a + b + c = 0, a + c = b,

3) 2х² — 5х + 3 = 0, 4) 3х² + 2х – 1 = 0,

a = 2, b = — 5 , c = 3 , a = 3 , b = 2 , c = — 1 ,

a + b + c = 0, a + c = b,

х₁ = 1, х₂ = х₁ = — 1, х₂ =

Вывод: при решении уравнения ах² + b х + c = 0 (a ≠ 0) можно пользоваться следующими утверждениями:

Если a + b + c = 0, то х₁ = 1, х₂ =

1) Разделим обе части уравнения на а ≠ 0 и получим:

х² + х + = 0.

2) По теореме Виета х₁ + х₂ = —,

х₁ · х₂ = ;

х₁ + х₂ = — = 1 + , х₁ = 1,

х₁ ∙ х₂ = 1 ∙ ; х₂ = .

Если a + с = b , то х₁ = — 1, х₂ = —

1) По теореме Виета х₁ + х₂ = —,

х₁ · х₂ = ;

2) Так как а +с = b , то

х₁ + х₂ = — = -1 –, х₁ = — 1,

х₁ · х₂ = -1 ∙ ( — ); х₂ = — .

Задание (устно). Найдите корни уравнения:

а) 3х² — 8х + 5 = 0; в) 5х² — 9х – 14 = 0;

б) 2х² + 3х + 1 = 0; г) — х² — 4х – 3 = 0.

Другой метод решения квадратных уравнений – метод «переброски» старшего коэффициента. Умножим обе части уравнения на а ≠ 0:

Пусть ах = у, тогда .

Корни у₁ и у₂ уравнения найдем по теореме, обратной теореме Виета. Так как

Пример. Решите уравнение

По теореме, обратной теореме Виета, имеем:

Замечание: Данный метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.

Задание на дом. Решите уравнения, используя с пециальные методы решения квадратных уравнений .

1907х 2 + 101х — 2008 = 0; х 2 + 12х + 20 = 0.

Тема 3. Графический способ решения квадратных уравнений

Графический способ решения квадратного уравнения состоит в построении на одной координатной плоскости графиков двух функций и нахождении абсцисс их точек пересечения (если такие точки есть).

В случае квадратного уравнения строятся графики квадратичной и линейной функций: парабола и прямая. Возможны следующие случаи (рис. 1):

1) прямая и парабола касаются (имеют единственную общую точку), абсцисса точки касания – корень уравнения;

2) прямая и парабола пересекаются в двух точках, абсциссы этих точек являются корнями уравнения;

3) прямая и парабола не имеют общих точек, в этом случае уравнение не имеет корней.

Источник