Способ группировки как правильно

Способ группировки

Способ группировке в алгебре — один из способов разложения многочлена на множители.

Способ группировки можно разбить на два этапа:

1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).

2) Вынесение полученного общего для всех групп множителя за скобки.

Группируем первое слагаемое со вторым, третье — с четвертым.

Лучше при группировке между скобками всегда ставить знак «+»:

Из первых скобок выносим общий множитель a, из вторых — -3. При вынесении «-» за скобки все знаки в скобках меняем на противоположные:

Общий множитель (x+7) выносим за скобки:

Группировать можно было иначе: первое слагаемое — с третьим, второе — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — 7:

Общий множитель (a-3) выносим за скобки:

При любом способе группировки ответ получается одинаковый (от перестановки мест множителей произведение не меняется).

Группируем первое слагаемое со вторым, третье — с четвертым:

Из первых скобок выносим общий множитель x, из вторых — «-«:

Общий множитель (4-y) выносим за скобки:

Внимание! Сколько слагаемых было до вынесения общего множителя за скобки, ровно столько же должно остаться после вынесения. Если общий множитель совпадает с одним из слагаемых (с точностью до знака), на месте этого слагаемого после вынесения общего множителя за скобки остается единица (+1 или -1).

Сгруппируем первое слагаемое со вторым и третьим, четвертое — с пятым и шестым:

Из первых скобок выносим общий множитель a, из вторых — -b:

Общий множитель (a²+1+b²) выносим за скобки:

Можно было группировать и по два слагаемых. Например, первое — с четвертым, второе — с пятым, третье — с шестым:

Из первых скобок выносим общий множитель a², во вторых скобках общего множителя нет, из третьих — b²:

Общий множитель (a-b) выносим за скобки. Не забываем поставить единицу на место (a-b)!

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник

Урок «Способ группировки»

Краткое описание документа:

Преобразование многочленов, состоящих из большого числа различных мономов, является одним из ключевых действий в линейной алгебре. При помощи этой процедуры решаются многие уравнения и развязываются неравенства. Правильное оперирование с многочленами позволяет также упрощать выражения функций и решать многие смежные комплексные задачи.

Поэтому в нашей серии видеоуроков мы продолжим рассматривать важнейшие аспекты преобразования полиномов, в частности, затронем такой метод, как группировку одночленов.

Как известно, одночлены представляют собой некое элементарное выражение, которое содержит переменную (или несколько переменных), числовой коэффициент и степень переменных. При этом коэффициент может быть равен нулю (буквенные значения без цифр), а переменные – отсутствовать (остается одно лишь число). Что бы перегруппировать одночлены, необходимо тщательно изучить их основу. Когда мы в предыдущем занятии выносили множитель за скобки, основа нужна была для утверждения самого множителя. В данном же случае по основе будет проводиться группировка одночленов для дальнейших преобразований.

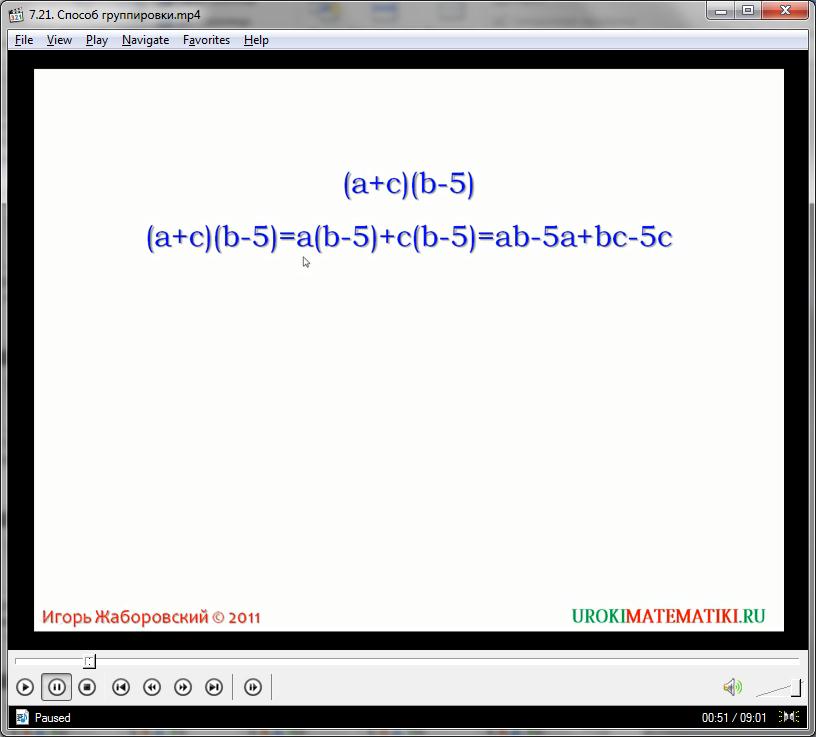
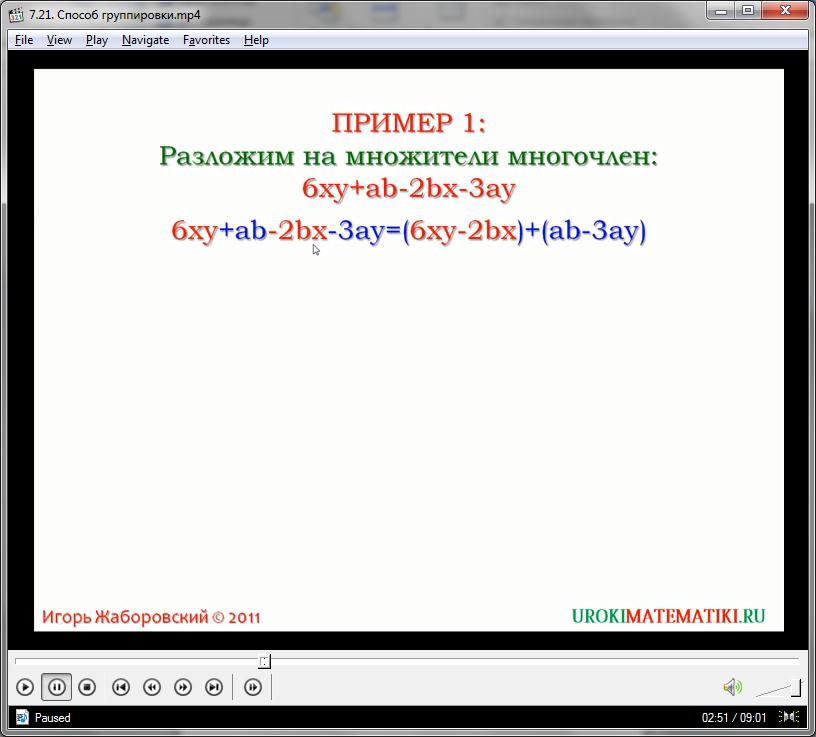
Существует правило, согласно которому выбирается такая основа, которая имеет максимально допустимую разрядность в том случае, если выбор её не продиктован внешними условиями комплексной задачи. Важно понять, что при применении способа группировки ищутся две или больше основ – для образования двух, или больше групп одночленов. Это коренное отличие данного метода от способа вынесения множителя за скобки. Хотя, в целом, ход дальнейших действий представляет собой вынесение основы за скобки (в которых заключена группа схожих одночленов), или схожие действия. Рассмотрим применение способа группировки на практике. Допустим, нам нужно преобразовать выражение:

2ас + 3ху + 8ау – 9хс

Стоит отметить, что способ группировки очень часто может дать несколько путей решения выражения. Особенно если многочлен содержит большое количество однотипных мономов. Группировать одночлены можно в любом порядке, соблюдая лишь правило наличия общей основы. Если сгруппировать выражение можно несколькими способами, то стоит выбирать наиболее оптимальный (чаще всего, подбирая группировку так, что бы получить необходимый для дальнейших вычислений элемент). В нашем примере, сгруппируем первый и третий члены многочлена, а также второй и четвертый. При этом первая группа имеет общую основу 2а (общая переменная а, наибольший допустимый числовой коэффициент), вторая группа – 3х. Группируем одночлены, выносим основы за скобки, произведя деление и не забывая про правила сохранения знаков:

2ас + 3ху + 8ау – 9хс = 2ас + 8ау + 3ху – 9хс = 2а(с+4у) + 3х(у – 3с)

Грубо говоря, числовой коэффициент множителя можно брать в виде абсолютно любого значения. Но чаще всего подбирают такое число, чтобы оно было кратным всем одночленам группы – это позволит избежать дробей.

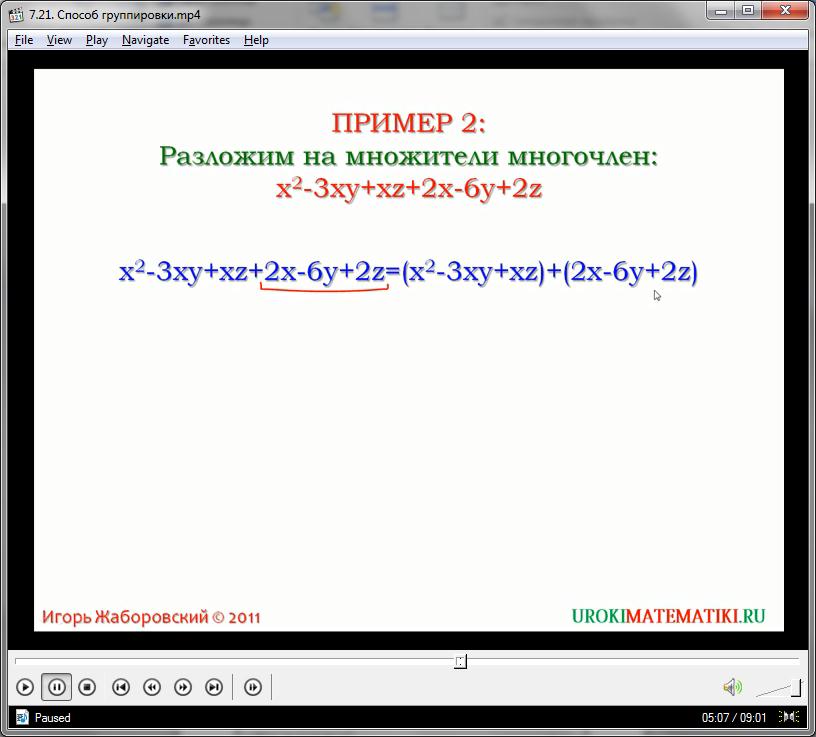
Рассмотрим ещё один пример, более сложный. Предположим, нам нужно разложить на множители полином вида:

Напрямую в этом выражении ничего вынести за скобки нельзя. Общий множитель для одного из членов отсутствует, а разность степеней переменных не позволяет полностью убрать х из группы первых двух мономов. Можно решить это выражение методом подбора. Представим произведение многочленов и решим его методом прямого перемножения (памятуя о строгой необходимости перемножить каждый член):

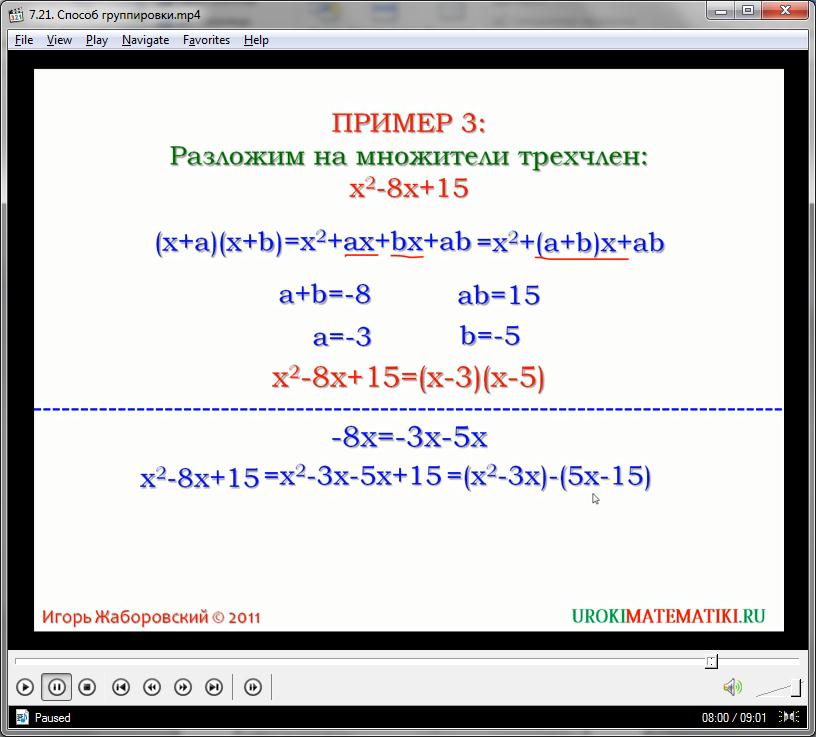
(х + а)(х + с) = х 2 + хс + ах + ас

Сгруппируем второй и третий члены полученного выражения, используя общую переменную х:

х 2 + хс + ах + ас = х 2 + х(а + с) + ас

Как заметно в видеоуроке, выражения х 2 – 8х + 15 и х 2 + х(а + с) + ас достаточно подобны между собой. Для их сравнения необходимо, чтобы коэффициент при х представлял собой сумму двух неких чисел а и с, которые в произведении дали бы свободный член полинома. Задачу нахождения этих чисел можно решить через подбор либо же использовать систему линейных уравнений:

Решив данную систему, получим, что уравнениям соответствует пара чисел -3 и -5. Так как они везде участвуют только в операциях сложения и произведения (где последовательность операндов роли не играет), то очередность а и с не имеет значения. Можно записать, что а=-3, с=-5. Тогда:

х 2 + хс + ах + ас = х 2 – 8х + 15

С другой стороны:

х 2 + хс + ах + ас = (х + а)(х + с)

В итоге получаем:

х 2 – 8х + 15 = (х + а)(х + с)

где а=-3, с=-5, подставляя значения переменных:

х 2 – 8х + 15 = (х – 5)(х – 3)

В дальнейших уроках можно будет узнать, что некоторые формулы, состоящие из стандартных переменных в многочленах, являются особой группой выражений, именуемых формулами сокращенного умножения.

Источник