Графический метод учета теплообмена калориметра с окружающей средой.
Какой бы хорошей ни была теплоизоляция калориметра, при калориметрических измерениях нельзя избежать теплообмена с окружающей средой. Предлагаемый метод учета теплообмена сводится к замене реального процесса фазового перехода, длящегося конечное время, идеализированным «мгновенным» процессом поглощения тепла льдом.
Графический метод учета теплообмена основан на эмпирическом законе Ньютона, который заключается в том, что скорость теплопередачи пропорциональна разности температур системыt и среды tср, если эта разность невелика:
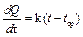 , при (t –tср) t, либо отдает при tср τ2 (рис. 12.1в). , при (t –tср) t, либо отдает при tср τ2 (рис. 12.1в). Рассмотрим процессы, происходящие при плавлении льда в калориметре, и изобразим графически зависимость температуры нашей системы (калориметр со льдом) от времени (рис. 12.2). Проведем опыт следующим образом. Возьмем калориметр со льдом, имеющий температуру приблизительно на 10°С выше комнатной. На начальном этапе от моментаτ = 0 до τ=τ1 происходит понижение температуры системы за счет теплообмена с внешней средой – участок АВ. В момент τ1 в калориметр опустим лед, имеющий температуру 0°С. Льда необходимо взять столько, чтобы при его плавлении температура системы опустилась ниже температуры среды. Интервал времени от τ1 до τ2 – основная стадия опыта (участок BNE), за это время происходит плавление льда. Начиная с момента τ2 , температура системы будет повышаться в результате получения тепла извне – на графике участок EF. Ординаты точек В и Е есть соответственно температура воды в калориметре в момент опускания льда (t0) и в момент окончания плавления (t1). Кривая ABNEF описывает реальный процесс, обозначим его I. Экстраполируем участок графика АВ на область τ > τ1 линией BCL – так изменилась бы температура системы, если бы в калориметр не был положен лед (при τ→ ∞ температура системы стремится к температуре среды), обозначим этот процесс II. Экстраполируем участок EF на область τ и в точке D –t1‘ . Площадь S1, ограниченная отрезком CH , прямой t=tсри кривой СL пропорциональна количеству теплоты, отданному в среду калориметром с водой при их остывании отt0‘ до tср, т.е.
Площадь S2 ограниченная отрезком HD, прямой t=tср и кривой DEFM пропорциональна количеству теплоты, полученному из среды при нагревании от t1‘ до tср калориметром с водой и водой, получившейся при плавлении льда, т.е.
Знак « — » указывает на то, что в этом случае система получала тепло из среды. Но по построению S1 +S2=SODE—SOBC=S, следовательно
что после приведения подобных членов приводит к уравнению для определения удельной теплоты плавления льда:
Следовательно, для решения задачи необходимо определить величины t0‘ и t1‘ , что делается с помощью экспериментального графика и описанных выше дополнительных построений. Источник 4.7 Определение измерения температурыДля измерения разности температур (ΔТ).служит метастатический термометр, известный под названием термометра Бекмана. Его особенностью является наличие в верхней части термометра дополнительного резервуара, в который при желании может быть переведена часть ртути из основного резервуара. Это дает возможность использовать один и тот же термометр для проведения измерений в разных интервалах температур. Шкала такого термометра охватывает интервал температур в 5-6º и разделена на деления, соответствующие 0,01º. Разумеется, при различных наполнениях ртутью основного резервуара термометра 1º шкалы его будет отвечать различным интервалам температуры. Таким образом, следует помнить, что шкала такого термометра имеет лишь условный характер, и для перевода разности температур, отмеченной по термометру, к действительному значению разности температур необходимо ввести поправку на так называемое «значение градуса». Эта поправка обычно дается в паспорте термометра для различных интервалов температур (т.е. для различных наполнений ртутью резервуара). Настройка метастатического термометра, шкала которого охватывает 5º , на нужный диапазон температур производится следующим образом. Предположим, требуется применить термометр в интервале температур 20 — 25º, т.е. нуль шкалы термометра должен соответствовать 20º С. Держа термометр в руках в наклонном положении (главный резервуар должен быть выше дополнительного) и слегка постукивая по нему пальцем (для преодоления трения ртути о стенки капилляра), добиваются того, чтобы ртуть начала перетекать из главного резервуара в дополнительный. Затем, повернув термометр главным резервуаром вверх и слегка встряхивая его, заставляют ртуть, находившуюся ранее в дополнительном резервуаре, соединиться с ртутью, выступающей из капилляра; затем осторожно, не встряхивая термометра, переводят его в нормальное положение (главным резервуаром вниз) и переносят в ванну (стакан с водой, имеющий температуру на 6º выше заданной, т.е. в нашем случае 26º С). Эта операция должна быть проделана так осторожно, чтобы столбик ртути в дополнительном резервуаре не разрывался. Выждав некоторое время, необходимое для выравнивания температур термометра и ванны, резко встряхивают термометр и заставляют ртуть, находящуюся в дополнительном резервуаре, упасть на дно. После этого термометр вынимают из ванны и дают охладиться, — держа в вертикальном положении, чтобы избежать возможности соединения ртути, находящейся в главном резервуаре, с ртутью, оставленной в дополнительном резервуаре. Какой именно температуре соответствует теперь метка «0» термометра, определяется сравнением его с проверенным термометром. В нашей работе используется довольно точный (точность до 0,01º) электронный термометр на сопротивлении. В ходе калориметрического опыта, проводимого в изотермическом калориметре, происходит теплообмен с окружающей средой, следствием чего являются тепловые потери в окружающую среду. Определить действительное значение ΔТ по данным, полученным в результате калориметрического опыта можно двумя способами: аналитическим и графическим. В нашей работе принят графический метод определения ΔТ, как более простой, по надежности не уступающий аналитическому. Температура калориметрической системы во время опыта изменяется как за счет теплоты процесса, так и вследствие теплообмена со средой (оболочкой) и нагревания при перемешивании. Таким образом, измеренное измерение температуры ΔTизм отличается от истинного Т; отвечающего теплоте изучаемого процесса. Характер теплообмена определяют по временному ходу температуры в течение каждого опыта. Поправку на теплообмен вводят либо аналитически, либо с помощью описываемого ниже графического метода Ланге-Мищенко. Если продолжительность опыта не превышает двадцати минут, то второй способ предпочтителен. Весь опыт делят на 3 периода (рисунок 4): предварительный, продолжающийся не менее 5 минут, главный с продолжительностью, зависящей от скорости реакции и скорости перемешивания, и заключительный, продолжающийся также не менее 5 минут. Рисунок 4 Графическое определение T Для опытов следует пользоваться дистиллированной водой, отмеряя ее мерным цилиндром. Количество воды определяется размером калориметра. Воду вливают во внутренний стакан калориметра (необходимо, чтобы температура воды в калориметре отличалась от температуры комнаты не более, чем на 1,0°С. Затем, производят измерение температуры калориметра через равные промежутки времени (30 сек). Время отмечается по секундомеру. Первые 11 отсчетов температуры составляют так называемый «начальный» период опыта. Его назначение — измерить «ход» температуры калориметра, т.е. изменение его температуры со временем до начала теплового процесса в калориметре. Этот «ход» должен быть постоянен, т.е. разность между последовательными отсчетами не должна различаться более, чем 0,001 — 0,002°. Предварительный период начинается с момента, когда изменение температуры становится постоянным и не превышает ±0,050 — 0,040 °С/мин (в противном случае следует изменить перепад температур оболочки и реактора). Измерения при постоянном ходе температуры производят десять раз, а через следующие 30 сек. проводят реакцию (например, смешивают жидкости) или включают нагреватель. С этого момента начинается главный период, в котором, как и в начальном периоде, продолжают проводить отсчеты температуры калориметра через каждые 30 сек. Главный период обычно длится 3-4 мин. Главный период опыта следует считать законченным, когда изменение температуры со временем становится постоянным. После этого производят еще 10 — 20 отсчетов температуры, составляющих так называемый «конечный» период опыта. Положим, что изучаемый процесс является экзотермическим: температура быстро повышается, а затем постепенно вновь устанавливается равномерный ход температуры. Переход к нему определяет начало заключительного периода. В заключительном периоде отсчеты температуры продолжают еще 5 мин. Если по окончании изучаемого процесса температура оболочки все еще выше температуры реактора, то в заключительном периоде температура продолжает повышаться (с меньшей скоростью, чем в предварительном). Если температура реактора превысит температуру оболочки, то в заключительном периоде температура падает. График строят в масштабе: 1-2 мм соответствует 0,01°С (см. рисунок 4). По оси температур можно сделать разрыв. На рисунке 1 измерение начато в момент, отвечающий точке b. Если бы тепловой эффект в реакторе не возникал, то температура продолжала бы расти по направлению прямой ab. В точке d начался заключительный период — температура падает линейно. Допускают, что в первой половине главного периода наклон прямой отвечает закону теплопередачи в предварительном периоде, а во второй половине — закону заключительного периода. Поэтому продолжают прямые ab и de до пересечения в точках с и с’ с вертикалью, проведенной через середину главного периода. Тем самым к T прибавляют величину, потерянную за счёт охлаждения при теплообмене (точка с лежит выше точки d), и вычитают эту величину, приобретенную за счет нагревания при перемешивании и теплообмене (тоска с’ выше точки b). Таким образом, находят T = cc’. Источник Графический и табличный методы анализа тепловых процессов в задачах по физике. Графический и табличный методы анализа тепловых процессов в задачах по физике. Описаны методы и приёмы, используемые автором в своей практической деятельности, при изучении тепловых явлений в 8-м и 10-м классах. Примеры и иллюстрации, приведённые в данном материале, позволяют продемонстрировать образцы решения задач по термодинамике. В педагогической деятельности учителя физики приходится достаточно часто сталкиваться с трудностями понимания учащимися анализа тепловых процессов. В результате, казалось бы, простые задачи оказываются нерешенными. А ведь с уравнением теплового баланса в курсе физики школьники встречаются дважды: в 8-м и в 10-м классах, причём сложность изучения данной темы в старших классах возрастает в разы. Но если в основной школе ученик не понял чего-то, то в 10-м классе всё приходится начинать сначала. При поиске решения данных проблем нужно учитывать два важных параметра: Методы решения должны быть наглядными и универсальными; Доступными для понимания и применения большинству учащихся непрофильных классов. Анализ учебно-методической литературы и контрольно-измерительных материалов показал, что графическое представление тепловых процессов позволяет значительно упростить поиск решения и составление уравнений, а также выявить скрытые процессы, т.е. обнаружить подводные камни. В статье представлено обобщение опыта работы автора по теме «Тепловые явления» Уравнение теплового баланса. Изменение агрегатных состояний вещества Многие обучающиеся испытывают сложности при составлении уравнений для решения задач, в которых происходит теплообмен между несколькими телами с учётом изменения агрегатного состояния этих тел. Можно использовать схемы, отображать процессы с помощью кругов, но, как выяснилось, все эти способы выраженного положительного эффекта не дают. Перед тем как перейти к непосредственному рассмотрению приёмов решения задач по теме «Тепловые явления», нужно отметить три важных замечания по методике изложения и изучения данной темы: Необходимо изначально показать обучающимся важность составления и записи уравнения теплового баланса в общем виде: Научить различать процессы, сопровождающиеся выделением и поглощением теплоты, и подставлять в уравнение с учётом отданного и полученного количества теплоты. Научить читать графики изменения температуры агрегатного состояния вещества. Методика решения подобных задач с учётом перехода из одного агрегатного состояния в другое у каждого учителя своя, но любому учителю физики всегда важно рассмотреть и альтернативную точку зрения. Плюсы и минусы своих вариантов всегда становятся более заметными в сравнении с предложениями коллег. Предлагаю рассмотреть метод, состоящих всего из двух этапов: Графическая интерпретация условия задачи. Составление уравнения теплового баланса для данной задачи, используя график, после чего начинается непосредственное математическое решение задачи. В качестве примера рассмотрим несколько задач, начиная с самой простой с постепенным усложнением. Обязательным условием в задачах будет наличие двух и более тел. Задача №1 (без изменения агрегатных состояний веществ): В латунный калориметр массой 128 г, содержащий 240 г воды при температуре 8,4 0 С, опущено металлическое тело массой 192 г, нагретое до 100 0 С. Окончательная температура, установившаяся в калориметре, 21,5 0 С. Определите удельную теплоёмкость испытуемого тела [1]. Решение: Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет три слагаемых. Для удобства можно записать уравнения для каждого участка в отдельности: Составляем уравнение согласно графику: И вот теперь начинается самое важное – математическое решение задачи. На первых же занятиях нужно обозначить целесообразность решения задачи в общем виде. Показать на примерах, что решение по действиям веет к округлениям, и как следствие – неправильному ответу. Ведь подстановка данных в выраженную из формулы величину позволяет быстро и безошибочно получить верный результат. Задача №2 (с изменением агрегатных состояний веществ): Смесь, состоящую из 5 кг льда и 15 кг воды при общей температуре 0 0 С, нужно нагреть до температуры 80 0 С пропусканием водяного пара при температуре 100 0 С. Определить необходимое количество пара [1]. Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет пять слагаемых. Для удобства можно записать уравнения для каждого участка: Составляем уравнение согласно графику: Задача №3 (с изменением агрегатного состояния части одного из веществ): В бак, содержащий воду массой 10 кг при температуре 20 0 С, бросили кусок железа массой 2 кг, нагретый до температуры 500 0 С. При этом некоторое количество воды превратилось в пар. Конечная температура, установившаяся в баке, равна 24 0 С. Определить массу воды, обратившейся в пар [1]. Графически показываем изменение температуры всех тел, указанных в задаче. Видно, что в уравнении теплового баланса будет четыре слагаемых. Для удобства можно записать уравнения для каждого участка: Составляем уравнение согласно графику: Данный метод позволяет наглядно увидеть, что происходит в задаче с веществами и какие уравнения необходимы для решения задачи. Первый закон термодинамики для изопроцессов и КПД тепловой машины. Данная тема при своей простоте, вызывает серьёзные затруднения у выпускников при решении задач 28 и 30 части 2 ЕГЭ по физике. Так же, как и в предыдущем случае, предлагаемый метод предполагает выполнение следующих задач: Научить обучающихся анализировать графики тепловых процессов для начала с помощью таблицы (для начала). Быстро определять в различных осях координат ( p , V , T ) максимальные и минимальные значения температуры, давления и объёма газа. Использовать уравнение Клапейрона-Менделеева для выражения внутренней энергии или работы газа через другие величины. Научить определять работу газа на участке как площадь фигуры под ним в координатах p ( V ) . Все эти навыки отрабатываются на каждом уроке в течение всего процесса изучения молекулярной физики газов. Необходимый уровень навыков достигается в течение нескольких занятий, после чего данный метод решения ложится в основу обобщения изученных приёмов и при подготовке к ЕГЭ ученик уже имеет необходимые знания и навыки, что позволяет сконцентрироваться на более детальном рассмотрении задач повышенной сложности. Метод анализа тепловых процессов с позиции термодинамики состоит из двух этапов: Анализ замкнутого цикла и заполнение расширенной таблицы. Составление необходимых соотношений, уравнений согласно условия задачи с опорой на анализ. Рассмотрим по аналогии с предыдущими задачами несколько типовых задач по термодинамике, применив к ним данный метод решения. Задача №1 (определение участков, где выделялась или поглощалась теплота): Определите на каком участке графика газу сообщалась теплота и вычислите её значение? Анализируем график и заполняем таблицу. Из таблицы видно, на каких участках к системе подводилась теплота, а на каких отводилась. В дальнейшем можно подвести учащихся к осознанию того, что и без таблицы можно быстро определять, что теплота подводится на тех участках где происходит увеличение температуры или объёма газа. Однако надо быть аккуратным с таким утверждением и помнить об адиабатном расширении или сжатии, т.к. в таком случае никакого теплообмена не происходит. Из таблицы выводим уравнение для расчёта количества теплоты, поступившей от нагревателя или наоборот отдаваемой в окружающую среду: Для решения задачи остаётся лишь воспользоваться изученным уравнениями. По поводу возможного замечания о том, что при передаче теплоты холодильнику в уравнении должен быть знак «минус», можно ответить, что он появится автоматически, если ученик будет правильно выполнять расчёт изменения внутренней энергии и работы газа. Необходимо помнить, что при вычислении любого изменения необходимо отнимать начальное значение от конечного, это же касается расчёта работы газа как площади фигуры по графику процесса в осях p ( V ) . Задача №2 (определение изменения каких-либо макропараметров): Как изменялась температура газа на каждом участке? Опишите процессы, происходящие с газом. Анализируем график и заполняем таблицу. Из таблицы видно, как менялась внутренняя энергия и количество теплоты, на основании табличных данных делается описание процессов и изменение температуры. Задача №3 (расчёт КПД тепловой машины): Определите КПД тепловой машины. Полезную работу газа по данному графику определить очень просто, она равна площади фигуры цикла. А вот количество теплоты, подводимой к системе определить можно двумя способами. Самый быстрый – посмотреть на каких участках было увеличение температуры и объёма. Из графика видно, что изотерма, проходящая через точку 2 выше чем изотермы, проведённые через точки 1 и 3. А изотерма в точке 1 ниже чем в точке 3. Участок 2-3 изохорный процесс, поэтому количество теплоты сообщалось только на участке 1-2. К данному выводу, можно прийти и через таблицу: Составляя уравнение КПД необходимо записать выражения изменения внутренней энергии и работы газа через p 0 и V 0 , тогда они сократятся и останется только числовое выражение. Данная методика позволяет анализировать более сложные задачи и находить нюансы которые могут быть упущены при беглом просмотре условия задачи. Рассмотрим пример такой задачи. Задача №4 (расчёт КПД тепловой машины): Определите КПД тепловой машины. Данная задача может показаться простой для ученика, но в ней есть один важный момент. При расчёте количества теплоты сообщаемой нагревателем, необходимо рассчитать положительное изменение внутренней энергии. А на данном графике, не каждый ученик сможет увидеть, что на участке 1-2 было увеличение температуры. Большая часть учащихся увидев данный участок, воспользовавшись уравнением состояния идеального газа обнаружит, что температура в точке 2 меньше температуры в точке 1, а значит было уменьшение внутренней энергии и не станут учитывать её изменение на этом участке. На самом же деле, мы имеем дело с процессом, где температура меняется по нелинейному закону (квадратичная зависимость). Температура увеличивалась от точки 1 до точки М. После чего начиналось уменьшение внутренней энергии. Таким образом количество теплоты полученной от нагревателя будет определяться как: Заполняя таблицу, ученики не проводя вышеописанного анализа, столкнулись бы с вопросом, как заполнить ячейку количества теплоты на участке 1-2, это послужило бы для них сигналом, что необходим детальный анализ данного участка. Дальнейшие действия по решению данной задачи выходят за рамки темы статьи. Заметим, что здесь необходимо использовать знания из математики о линейной функции, участком которой является отрезок 1-2. Получив функциональную зависимость давления от объёма на этом участке, необходимо подставить её в уравнение Клапейрона-Менделеева и задача будет решена. Приведенные выше методы решения задач на тепловые являения, при должном усердии и кропотливой работе учителя над формированием необходимых умений у обучающихся позволяют подготовить учеников к решению более сложных задач по тепловой физике и нивелировать их страх перед сдачей выпускного экзамена по физике. Но главным является то, что использование этих приёмов приводит к развитию нестандартного, творческого мышления школьника, независимо от профиля его обучения. Надеемся, что предложенные приёмы решения задач по термодинамике помогут сделать изучение тепловых процессов более простым и понятным, будут способствовать формированию исследовательских навыков при решении задач и окажут положительное воздействие на интеллектуальное развитие школьников. Список использованной литературы Кирик, Л.А. Физика-8. Разноуровневые самостоятельные и контрольные работы. – Харьков.: «Гимназия», 2001. – 144 с. Источник |

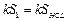
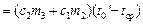 .
.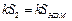
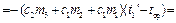
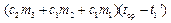
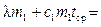
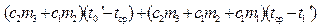 ,
,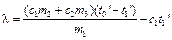 .
.






























