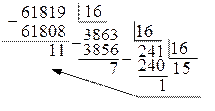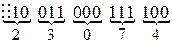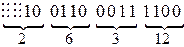Способ горнера примеры для системы счисления
    Рассмотрим развернутую запись числа в троичной системе счисления: 12012 3 =1*3 4 +2*3 3 +0*3 2 +1*3 1 +2*3 0 . В первых четырех слагаемых имеется общий множитель 3, который можно вынести за скобки. Получим:
    1*3 4 +2*3 3 +0*3 2 +1*3 1 +2*3 0 =(1*3 3 +2*3 2 +0*3 2 +1)*3+2. Теперь этот же множитель можно вынести из первых трех слагаемых:
    1*3 4 +2*3 3 +0*3 2 +1*3 1 +2*3 0 =(1*3 3 +2*3 2 +0*3 1 +1)*3+2=((1*3 2 +2*3 1 +0)*3+1)*3+2. И, наконец:
    1*3 4 +2*3 3 +0*3 2 +1*3 1 +2*3 0 =(1*3 3 +2*3 2 +0*3 1 +1)*3+2=((1*3 2 +2*3 1 +0)*3+1)*3+2=(((1*3+2)*3+0)*3+1)*3+2.
    На основе этой схемы можно вывести следующий алгоритм для перевода целых чисел в десятичную систему счисления:
    Старшую цифру умножаем на основание, добавляем вторую цифру, результат умножаем на основание, добавляем третью цифру и так до тех пор, пока не прибавим последнюю цифру.
    Результатом будет десятичная запись числа. Ясно, что полученное равенство будет справедливо для любых целых P-ичных чисел, а формулу можно записать в общем виде:
a n a n-1 a n-2 . a 1 a 0 p =(. (a n *p+a n-1 )*p+a n-2 )*p+. )+a 1 )*p+a 0 .
    Эта формула и является иллюстрацией схемы Горнера для пероевода целых чисел в десятичную систему счисления.
    Механизм вычислений можно представить так ( на рассмотренном выше примере):
    1    2    0     1      2 (выписываем цифры числа в заданной системе счисления).
   1  5  15  46   140 (результат, полученный при умножении на основание и добавлении очередной цифры, записываем под соответствующей цифрой). Последнее число и будет ответом.
Действия над числами в различных системах счисления
    Действия над числами в различных системах счисления производятся на основе таблиц сложения и умножения в этих системах счисления. Самые простые таблицы сложения и умножения, конечно же, в двоичной системе счисления:    
| 1+0=1 | 1*0=0 |
| 1+1=10 | 1*1=1 |
    Немногим длиннее оказываются таблицы сложения и умножения в троичной системе счисления. Пропустим в них строки сложения с нулем и умножения на нуль:
| Таблица сложения | Таблица умножения | ||
| 1+1=2 | 1*1=1 | ||
| 1+2=10 | 2+2=11 | 1*2=2 | 2*2=11 |
    Более привычный для нас вид имеют таблицы сложения и умножения в восьмеричной системе счисления:
| Таблица сложения | ||||||
| 1+1=2 | ||||||
| 1+2=3 | 2+2=4 | |||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=10 | |||
| 1+5=6 | 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | ||
| 1+6=7 | 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | |
| 1+7=10 | 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
| Таблица умножения | ||||||
| 1*1=2 | ||||||
| 1*2=2 | 2*2=4 | |||||
| 1*3=3 | 2*3=6 | 3*3=11 | ||||
| 1*4=4 | 2*4=10 | 3*4=14 | 4*4=20 | |||
| 1*5=5 | 2*5=12 | 3*5=17 | 4*5=24 | 5*5=31 | ||
| 1*6=6 | 2*6=14 | 3*6=22 | 4*6=30 | 5*6=36 | 6*6=44 | |
| 1*7=7 | 2*7=16 | 3*7=25 | 4*7=34 | 5*7=43 | 6*7=52 | 7*7=61 |
    А теперь представьте, что в первом классе вам нужно было бы выучить наизусть таблицы сложения и умножения в шестнадцатеричной системе счисления! Сколько бы времени вы на это затратили?
| Таблица сложения | ||||||||||||||
| 1+1=2 | ||||||||||||||
| 1+2=3 | 2+2=4 | |||||||||||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||||||||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 | |||||||||||
| 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | 5+5=A | ||||||||||
| 1+6=7 | 2+6=8 | 3+6=9 | 4+6=A | 5+6=B | 6+6=C | |||||||||
| 1+7=8 | 2+7=9 | 3+7=A | 4+7=B | 5+7=C | 6+7=D | 7+7=E | ||||||||
| 1+8=9 | 2+8=A | 3+8=B | 4+8=C | 5+8=D | 6+8=E | 7+8=F | 8+8=10 | |||||||
| 1+9=A | 2+9=B | 3+9=C | 4+9=D | 5+9=E | 6+9=F | 7+9=10 | 8+9=11 | 9+9=12 | ||||||
| 1+A=B | 2+A=C | 3+A=D | 4+A=E | 5+A=F | 6+A=10 | 7+A=11 | 8+A=12 | 9+A=13 | A+A=14 | |||||
| 1+B=C | 2+B=D | 3+B=E | 4+B=F | 5+B=10 | 6+B=11 | 7+B=12 | 8+B=13 | 9+B=14 | A+B=15 | B+B=16 | ||||
| 1+C=D | 2+C=E | 3+C=F | 4+C=10 | 5+C=11 | 6+C=12 | 7+C=13 | 8+C=14 | 9+C=15 | A+C=16 | B+C=17 | C+C=18 | |||
| 1+D=E | 2+D=F | 3+D=10 | 4+D=11 | 5+D=12 | 6+D=13 | 7+D=14 | 8+D=15 | 9+D=16 | A+D=17 | B+D=18 | C+D=19 | D+D=1A | ||
| 1+E=F | 2+E=10 | 3+E=11 | 4+E=12 | 5+E=13 | 6+E=14 | 7+E=15 | 8+E=16 | 9+E=17 | A+E=18 | B+E=19 | C+E=1A | D+E=1B | E+E=1C | |
| 1+F=10 | 2+F=11 | 3+F=12 | 4+F=13 | 5+F=14 | 6+F=15 | 7+F=16 | 8+F=17 | 9+F=18 | A+F=19 | B+F=1A | C+F=1B | D+F=1C | E+F=1D | F+F=1E |
| Таблица умножения | ||||||||||||||
| 1*1=1 | ||||||||||||||
| 1*2=2 | 2*2=4 | |||||||||||||
| 1*3=3 | 2*3=6 | 3*3=9 | ||||||||||||
| 1*4=4 | 2*4=8 | 3*4=C | 4*4=10 | |||||||||||
| 1*5=5 | 2*5=A | 3*5=F | 4*5=14 | 5*5=19 | ||||||||||
| 1*6=6 | 2*6=C | 3*6=12 | 4*6=18 | 5*6=1E | 6*6=24 | |||||||||
| 1*7=7 | 2*7=E | 3*7=15 | 4*7=1C | 5*7=23 | 6*7=2A | 7*7=31 | ||||||||
| 1*8=8 | 2*8=10 | 3*8=18 | 4*8=20 | 5*8=28 | 6*8=30 | 7*8=38 | 8*8=40 | |||||||
| 1*9=9 | 2*9=12 | 3*9=1B | 4*9=24 | 5*9=2D | 6*9=36 | 7*9=3F | 8*9=48 | 9*9=51 | ||||||
| 1*A=A | 2*A=14 | 3*A=1E | 4*A=28 | 5*A=32 | 6*A=3C | 7*A=46 | 8*A=50 | 9*A=5A | A*A=64 | |||||
| 1*B=B | 2*B=16 | 3*B=21 | 4*B=2C | 5*B=37 | 6*B=42 | 7*B=4D | 8*B=58 | 9*B=63 | A*B=6E | B*B=79 | ||||
| 1*C=C | 2*C=18 | 3*C=24 | 4*C=30 | 5*C=3C | 6*C=48 | 7*C=54 | 8*C=60 | 9*C=6C | A*C=78 | B*C=84 | C*C=90 | |||
| 1*D=D | 2*D=1A | 3*D=27 | 4*D=34 | 5*D=41 | 6*D=4E | 7*D=5B | 8*D=68 | 9*D=75 | A*D=82 | B*D=8F | C*D=9C | D*D=A9 | ||
| 1*E=E | 2*E=1C | 3*E=2A | 4*E=38 | 5*E=46 | 6*E=54 | 7*E=62 | 8*E=70 | 9*E=7E | A*E=8C | B*E=9A | C*E=A8 | D*E=B6 | E*E=C4 | |
| 1*F=F | 2*F=1E | 3*F=2D | 4*F=3C | 5*F=4B | 6*F=5A | 7*F=69 | 8*F=78 | 9*F=87 | A*F=96 | B*F=A5 | C*F=B4 | D*F=C3 | E*F=D2 | F*F=E1 |
    Пользуясь таблицами, выполним: 31 8 +52 8 и 31 8 *52 8 . Применим обычное сложение и умножение «столбиком»: . Произведем проверку, переведя слагаемые (множители) и результаты в десятичную систему счисления по схеме Горнера:
   3    1       5   2        1   0   3          2   0     3       2
   3    25       5    42        1   8    67        2   16   131    1050
    Сложив в десятичной системе счисления числа 25 и 42, получим 67, а перемножив эти же числа, получим 1050, значит, действия выполнены правильно.
Источник
Способ горнера примеры для системы счисления
Урок 11. Схема Горнера и перевод чисел
1. Перевод целого числа десятичного кода в любую другую систему счисления осуществляется по следующему правилу: нужно делить исходное десятичное число на величину основания той системы счисления, в которую переводится число, а затем частное от деления снова делить на то же основание и так до тех пор, пока частное не окажется меньше делителя. Полученные остатки от деления и последнее частное будут представлять собой разряды числа в новой системе счисления. Чтение нового кода осуществляется с конца, т.е. последнее частное дает цифру старшего разряда.
Примеры:
1) перевести десятичное число 11 в двоичную систему счисления:
| — |
| — |
| — |
 |
 Направление чтения |
Искомое двоичное число 1011, т.е.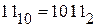 
.
2) перевести десятичное число 61819 в шестнадцатеричную систему:
Поскольку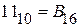 
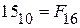
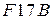
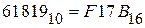
, а 
, искомое шестнадцатеричное число запишется в виде 
, т.е. 
.
2. Для перевода чисел из любой системы счисления в десятичную можно использовать запись этого числа в виде полинома (2.1). Выполнив сложение, получаем искомое десятичное число.
Пример.
Перевести восьмеричное число 745 в десятичную систему счисления:
.
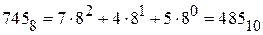
Перевод в десятичный код может быть выполнен также по схеме Горнера.Процедура перевода следующая. Старший разряд исходного кода нужно умножить на основание переводимой системы счисления и полученное произведение сложить со следующим символом кода. Полученную сумму вновь умножить на основание и результат сложить со следующим символом и так продолжать до последнего (младшего) разряда кода. Для числа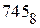 
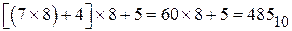
указанные вычисления будут следующими:
.
Схема Горнера особенно удобна при переводе чисел из двоичной системы. Имеем: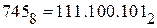 
. Переведем полученное двоичное число в десятичное:
Искомое десятичное число 485, т.е.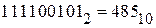 
.
3. Перевод чисел из любой недесятичной системы счисления в другую недесятичную систему выполняется в следующей последовательности:
– по методике, изложенной в п. 2, перевести исходный код в десятичный;
– по методике, изложенной в п. 1, перевести полученный десятичный код во вторую систему счисления.
Решение упрощается, если основания подлежащих переводу систем удовлетворяют условию (2.3), т.е.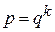 
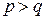
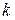
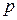
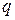
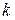
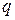
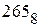
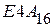
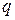
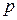
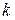
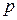
, где 
, 
– целое положительное число. При этом, если исходное число представлено в системе счисления с основанием 
, для получения его изображения в системе с основанием 
достаточно каждый символ исходного кода представить -значным числом в системе счисления с основанием . Примеры такого перевода приведены в п. 2.1.2 для чисел 
и 
. Если же исходное число представлено в системе счисления с основанием , для получения его изображения в системе с основанием нужно в последовательности символов исходного кода, начиная с младших разрядов, выделять группы по знаков и каждой из этих групп поставить в соответствие число в системе счисления с основанием . Если последняя группа окажется неполной, ее нужно дополнить нулями со стороны старших разрядов.
Примеры:
1) перевести двоичное число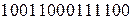 
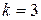
в восьмеричную систему счисления ( 
):
Получаем: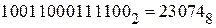 
;
2) перевести то же двоичное число в шестнадцатеричную систему счисления (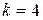 
):
Получаем: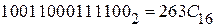 
.
Последние примеры показывают, что если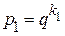 
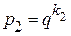
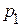
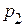
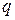
, а 
, перевод чисел из системы счисления с основанием 
в систему с основанием 
и наоборот может выполняться через промежуточную систему счисления с основанием . В частности, так можно осуществлять перевод чисел из восьмеричной системы в шестнадцатеричную и наоборот через двоичный код, т.е. сначала исходное число представляется в двоичном коде, затем полученная двоичная комбинация разбивается на группы, каждой из которых ставится число во второй системе счисления.
Источник
