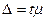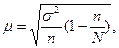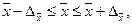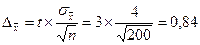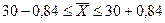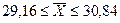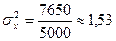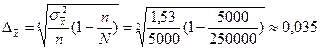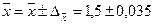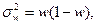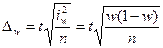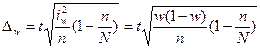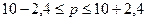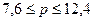Способы формирования выборочной совокупности
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор — в выборку отбираются отдельные единицы;
2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
- собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
- механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
- типическая – при которой генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность;
- серийная — при которой генеральную совокупность делят на одинаковые по объему группы — серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию;
- комбинированная — выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
В статистике различают следующие способы отбора единиц в выборочную совокупность:
- одноступенчатая выборка — каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки);
- многоступенчатая выборка — производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).
Источник
Способ формирования выборочной совокупности это
1.1.2. ВЫБОРОЧНЫЙ МЕТОД НАБЛЮДЕНИЯ.
СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ
Применение выборочного метода наблюдения включает следующие этапы:
определение генеральной совокупности и единиц наблюдения, обладающих первичной информацией, необходимой для решения задач обследования;
создание основы выборки;
формирование выборочной совокупности путем отбора элементов основы;
распространение собранных по выборке данных на генеральную совокупность.
Последний этап зависит от примененного способа отбора элементов в выборку и используемой формулы оценивания характеристик генеральной совокупности по данным выборки.
В статистической практике выборки извлекаются из конечных списочных основ. Однако единица основы, единица отбора и единица наблюдения могут отличаться. Например, это обычная ситуация при обследованиях населения и сельскохозяйственного сектора.
При рассмотрении любой схемы извлечения выборки должны быть учтены два фактора:
а) использовалась или нет вероятностная процедура;
б) наличие или отсутствие объективности в действиях специалиста, формирующего выборку.
Смысл объективности ясен и однозначен: любой специалист, производящий отбор, получил бы ту же самую выборку, т.е. выборку с теми же самыми свойствами. Субъективность означает, что специалисту, производящему отбор, позволено опираться на собственное суждение или интуицию относительно того, что является «хорошей» выборкой.
Рассматривая каждый из этих факторов на двух уровнях, можно выделить четыре типа выборок:
Роль, которую
играет специалист, осуществляющий отбор
Процедура отбора
Вероятностная
Невероятностная
Объективная
Выборки, сформированные вероятностным (случайным) образом
Выборки, сформированные на основе направленного отбора
Субъективная
Выборки, сформированные квазислучайным образом
Выборки, сформированные на основе суждения эксперта
В статистической практике используются все четыре типа выборок. Однако обычно отдают предпочтение вероятностным (случайным) выборкам как наиболее объективным, поскольку имеется хорошо обоснованная теория, позволяющая понимать поведение таких выборок и оценивать их свойства (качество) отображения характеристик всей совокупности. Свойства и объективная ценность других выборок известны в меньшей мере.
Имеются два типа выборок, основывающихся на вероятностном способе отбора: выборки, отбираемые по объективным правилам вероятностного (случайного) отбора, и выборки, отбираемые, строго говоря, не по этим правилам (квазислучайные). Материалы сборника содержат значительное число примеров использования в статистической практике объективных вероятностных выборок. Одно из наиболее ценных качеств вероятностных выборок состоит в том, что можно оценить точность получаемых результатов по данным самой выборки.
В теории выборочных обследований рассматриваются выборки, извлеченные из совокупностей (основ выборки), содержащих некоторое конечное число единиц N . Эти единицы различимы между собой и число различных выборок объема n , которые могут быть извлечены из списка N единиц, равно числу сочетаний .
В выборочных статистических обследованиях в целях расчета параметров совокупности основное внимание направлено на изучение определенных свойств единиц, которые измеряются и фиксируются в процессе наблюдения для каждой единицы, включенной в выборку. Эти свойства называют признаками.
Хотя выборка используется для многих целей, обычно представляют интерес четыре характеристики совокупности:
среднее значение признака (например, среднее число занятых на одном предприятии);
суммарное значение признака (например, выпуск продукции предприятиями промышленности);
отношение двух суммарных или средних значений (например, отношение стоимости ликвидных активов к общей стоимости активов);
доля единиц в совокупности, относящихся к некоторой определенной группе (например, доля промышленных предприятий, оказывающих платные услуги населению) или обладающих определенным значением признака.
Главным вопросом методологии выборочного наблюдения является обеспечение приемлемого уровня ошибок получаемых значений характеристик совокупности, в том числе по требуемым разрезам, например, отраслям экономики, формам собственности и регионам России.
Полученные в результате выборочного наблюдения характеристики практически всегда несколько отличаются от характеристик генеральной совокупности. Эти отличия называются ошибками выборки (или репрезентативности) , которые могут быть систематическими или случайными.
Систематические ошибки имеют место в том случае, когда нарушен принцип случайности отбора и в выборку попали единицы, обладающие какими-либо свойствами, не характерными для всех единиц генеральной совокупности. Случайные ошибки обусловлены тем обстоятельством, что даже при тщательной организации выборка не может в точности воспроизвести генеральную совокупность. В отличие от ошибок систематических, случайные ошибки являются вполне допустимыми, если они малы и могут быть оценены статистически.
Для измерения ошибки выборки, а также сравнения двух оценок, т.е. выявления более эффективной оценки, используют средний квадрат ошибки оценки (СКО), который измеряет ошибку относительно оцениваемого параметра совокупности:
символ, заменяющий выражение «математическое ожидание величины»;
оценка некоторой характеристики совокупности , получаемая согласно некоторой схеме отбора и примененной формуле оценивания;
математическое ожидание — среднее значение, взятое по всем возможным выборкам;
смещение оценки;
дисперсия оценки.
Таким образом, СКО является критерием достоверности оценки, который характеризует величину отклонений от истинного значения характеристики совокупности .
Поскольку на практике трудно проследить, чтобы оценки не давали никаких смещений, для характеристики оценки используется понятие «точности», относящееся к величине отклонений от усредненного значения .
Степень точности оценки обычно характеризуется ее дисперсией, стандартной ошибкой, коэффициентом вариации (относительной стандартной ошибкой) и доверительным интервалом.
Точность какой-либо оценки, полученной по выборке, зависит от двух факторов: от способа, которым оценка вычисляется по данным выборки, и от способа формирования самой выборки.
В выборочных обследованиях способ оценивания называется состоятельным, если оценка становится в точности равной оцениваемому параметру для совокупности при n = N , т.е. когда выборку составляет вся совокупность. Очевидно, что при простом случайном отборе выборочное среднее и произведение представляют собой состоятельные оценки соответственно среднего и суммарного значений для совокупности.
В данном контексте способ оценивания называется несмещенным , если среднее значение оценки, взятое по всем возможным выборкам данного объема n , в точности равно истинному значению для совокупности, и это утверждение справедливо для любой конечной совокупности значений и для любого n . Например, при простом случайном отборе выборочное среднее — несмещенная оценка среднего значения признака, — несмещенная оценка суммарного значения Y для совокупности, где — среднее значение признака по выборке.
В теории и практике выборочных обследований часто приходится рассматривать смещенные оценки. Это обусловлено следующими причинами. Во-первых, в некоторых случаях, особенно при оценивании отношений двух величин, смещенные оценки дают более достоверные результаты, чем несмещенные. Во-вторых, даже в случае использования теоретически несмещенных оценок ошибки наблюдения и неполучение ответов от респондентов могут привести к смещениям в распространенных результатах.
Кратко опишем некоторые, наиболее часто используемые в статистической практике способы формирования вероятностной выборки.
Простой случайный отбор. Простым случайным отбором называется способ, при котором извлечение единиц из совокупности для обследования осуществляется методом жеребьевки или с использованием таблиц или генератора случайных чисел без деления этой совокупности на какие-либо классы или группы.
Простую случайную выборку получают, отбирая последовательно единицу за единицей. Единицы в совокупности нумеруются числами от 1 до N , после чего выбирается последовательность n случайных чисел, заключенных между 1 и N . Единицы совокупности, имеющие эти номера, составляют выборку. На каждом этапе отбора такой процесс обеспечивает для всех еще не выбранных номеров равную вероятность быть отобранными. Легко показать, что равную вероятность быть отобранными имеют все возможных выборок.
Уже отобранные номера исключаются из списка, иначе одна и та же единица могла бы попасть в выборку более одного раза. Поэтому такой отбор называется отбором без возвращения . Отбор с возвращением легко осуществим, но им, за исключением особых случаев, пользуются редко, поскольку нет особых оснований допускать, чтобы одна и та же единица встречалась в выборке дважды.
При простом случайном отборе для получения выводов о параметрах совокупности используют выборочное среднее в качестве оценки среднего значения признака совокупности, а дисперсию признака по выборке — для оценки дисперсии признака совокупности. Для простой случайной выборки усредненные выборочные средние и дисперсии точно равны среднему и дисперсии признака совокупности.
ФОРМУЛЫ ОЦЕНИВАНИЯ ПРИ ПРОСТОМ СЛУЧАЙНОМ ОТБОРЕ
Источник
Основные способы формирования выборочной совокупности
Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая, в свою очередь, зависит от способа отбора единиц из генеральной совокупности. В каждом конкретном случае в зависимости от целого ряда условий, а именно, сущности исследуемого явления, объема совокупности, вариации и распределения наблюдаемых признаков, материальных и трудовых ресурсов, выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе — группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отбора.
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.
Бесповторнымназывается отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
При повторномотборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора. Повторный метод отбора применяется в тех случаях, когда характер исследуемого явления предполагает возможность повторной регистрации единиц- Такая возможность, прежде всего, может иметь место в выборочных обследованиях населения в качестве покупателей, пациентов, избирателей, абитуриентов и т.д.
Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее распространение получили следующие виды выборки:
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Для жеребьевки необходимо подготовить достаточное количество жребиев — фишек, шаров, карточек, соответствующее объему генеральной совокупности. Каждый жребий должен содержать информацию об отдельной единице совокупности — номер, фамилию лица или адрес, название или какой-либо другой отличительный признак. Необходимое в соответствии с установленным процентом отбора количества жребиев извлекается из общей их совокупности в случайном порядке.
При отборе по таблицам случайных чисел каждая единица генеральной совокупности должна иметь порядковый номер. Таблицы случайных чисел получаются с помощью датчика случайных чисел на ПК и представляют собой абсолютно произвольные столбцы цифр. В соответствии с объектом генеральной совокупности выбирается любой столбец с числами необходимой значимости. Например, если генеральная совокупность включает 5000 единиц, потребуется четырехзначные столбцы, при этом числа больше 5000 не будут приниматься во внимание. В выборочную совокупность отбираются единицы с порядковыми номерами, соответствующими числам выбранного столбца.
Собственно-случайный отбор может быть как повторным, так и бесповторным. Для проведения бесповторного отбора в процессе жеребьевки выпавшие жребии обратно в исходную совокупность не возвращаются и в дальнейшем отборе не участвуют. При использовании таблиц случайных чисел бесповторность отбора достигается пропуском чисел в случае их повторения в выбранном столбце или столбцах.
После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.
Эти два вида ошибок связаны следующим соотношением:
где ∆ — предельная ошибка выборки;
µ — средняя ошибка выборки;
t – коэффициент доверия, определяемый в зависимости от уровня вероятности p.
Ниже приведены некоторые значения t.
Вероятность 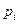 | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле:
,
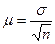
а при бесповторном:
где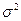 
— выборочная (или генеральная) дисперсия;
σ – выборочное (или генеральное) среднее квадратическое отклонение;
n – объем выборочной совокупности;
N – объем генеральной совокупности.
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
где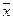 
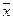
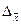
и — генеральная и выборочная средняя соответственно;
— предельная ошибка выборочной средней.
Покажем практическое применение рассмотренной выше методики на следующих примерах.
Пример 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при p = 0,997 t = 3, она равна:
Определим пределы генеральной средней:
Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
| Число детей в семье |
| Количество семей |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. Вначале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Число детей в семье, 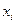 | Количество семей,  |  |  |  |  |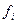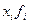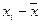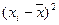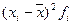
| -1,5 -0,5 0,5 1,5 2,5 3,5 | 2,25 0,25 0,25 2,25 6,25 12,25 | ||||
| Итого | — | — |
(чел.); 
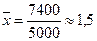
Вычислим теперь предельную ошибку выборки (с учетом того, что при p = 0,954 t = 2).
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:
где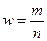 
— доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:
Соответственно, при повторном отборе:
Пределы доли признака в генеральной совокупности p выглядят следующим образом:
Пример 3.С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 200а г. была проведена 25%-ная случайная бесповоротная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение.Определим объем выборочной совокупности:
n = 480 × 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при p = 0,683 t = 1, вычислим предельную ошибку выборочной доли:
или 2,4%
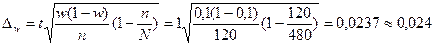
Пределы доли признака в генеральной совокупности:
Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности в 500 000 единиц предполагается получить 2%-ную выборку, т.е. отобрать 10 000 единиц, то пропорция отбора составит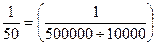 
. Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или с его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно отбор начинать с середины первого интервала, например, при 5%-ной выборке отобрать 10-ю, 30-ю, 50-ю, 70-ю и с таким же интервалом последующие единицы.
Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случайном бесповторном отборе.
Типический отбор. Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий — отрасль или подотрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.
Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.
При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
,
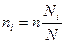
где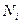 
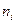
— объем i-ой группы;
— объем выборки за i-ой группы.
Средняя ошибка такой выборки находится по формулам:
(повторный отбор)
(бесповторный отбор)
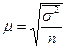
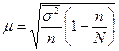
где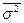 
— средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:
,
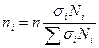
где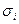 
— среднее квадратическое отклонение признака в i-ой группе.
Средняя ошибка такого отбора определяется следующим образом:
(повторный отбор)
(бесповторный отбор)
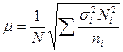
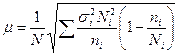
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 8.3.).
Источник
