Детерминированное моделирование факторных систем
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования факторных систем заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Источник
Преобразование моделей
В экономическом анализе часто используются различные способы преобразования кратных детерминированных моделей:
§ формальное разложение модели;
1. Удлинение модели — это процедура разложения числителя на сумму отдельных факторов
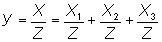
Например, себестоимость единицы продукции — это отношение суммарных затрат к объему продукции в натуральном выражении, и тогда модель имеет следующий вид:
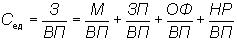
где Сед — себестоимость единицы продукции;
З — общая величина затрат;
ВП — выпуск продукции;
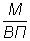
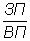
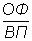
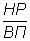
Полученная в результате процедуры удлинения новая модель имеет совершенно самостоятельные экономические показатели.
2. Способ формального разложения модели состоит в удлинении знаменателя исходной модели путем замены его на сумму или произведение отдельных факторов:
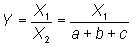
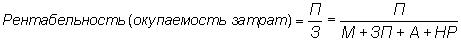
3. Расширение модели. Исходная модель расширяется за счет умножения числителя и знаменателя на один или несколько показателей, после чего полученная модель содержит набор новых факторов.
Например, если преобразовать формулу рентабельности активов, введя множитель РП / РП, то она примет следующий вид:
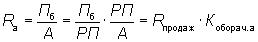
4. Способ сокращения модели состоит в создании новой модели путем деления числителя и знаменателя на один и тот же показатель Например, если числитель и знаменатель формулы фондорентабельности разделить на величину выручки от реализации, то новая модель будет иметь в числителе рентабельность продаж, а в знаменателе — фондоемкость продукции:
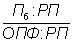
где Пб : РП — рентабельность продаж;
ОПФ : РП — фондоемкость продукции.
На практике для преобразования одной и той же модели могут использоваться различные способы, часто смешанные.
Источник
Электронная библиотека
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, определяющими их величину. Моделирование – это метод научного познания, с помощью которого создается модель объекта исследования. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического выражения.
В факторном анализе используются модели двух типов:
С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем и факторами. При создании детерминированных факторных моделей необходимо учитывать следующие требования:
1) факторы, включаемые в модель, должны реально существовать;
2) факторы, входящие в модель, должны находиться в причинно-следственной связи с изучаемым показателем;
3) все показатели факторной модели должны быть количественно измеримыми;
4) факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют четыре типа факторных моделей:
Они используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей;
Этот тип моделей применяется, когда результативный показатель представляет собой произведение нескольких факторных показателей;
Модель применяется в том случае, когда результативный показатель получают делением одного факторного показателя на величину другого;
1) смешанные (комбинированные) – это сочетание в различных комбинациях предыдущих моделей:
Моделирование мультипликативных и аддитивных факторных систем осуществляется путем расширения. Например, при исследовании процесса формирования объема производства продукции применяют следующие детерминированные модели:
ВП = ЧР * Д * П * ЧВ,
где ВП – выпуск продукции; ЧР – численность рабочих; ГВ – годовая выработка рабочего; Д – количество дней, отработанных одним рабочим за год; ДВ – дневная выработка рабочего; П – продолжительность рабочего дня; ЧВ – часовая выработка рабочего.
Аналогичным образом, т.е. путем расчленения одного из факторных показателей на составные элементы, осуществляется моделирование аддитивных факторных систем.
Как известно, объем реализации продукции равен:
где ВП – объем выпуска продукции; Он.п – остатки нереализованной продукции.
Часть нереализованной продукции может находиться на складах предприятия (Oскл), а часть может быть отгружена покупателям, но еще не оплачена (Оотг). Тогда приведенную исходную модель можно записать следующим образом:
К кратным моделям применяют следующие способы преобразования:
Способ удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей.
Например, себестоимость единицы продукции можно представить в виде функции двух факторов: изменения суммы затрат (З) и объема выпуска продукции (BП):
Если общую сумму затрат (З) разложить на элементы, такие, как заработная плата (ЗП), материальные затраты (МЗ), амортизация основных средств (А), накладные расходы (HР), то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:
где x1 – трудоемкость продукции; x2 – материалоемкость продукции; х3 – фондоемкость продукции; x4 – уровень накладных расходов.
Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей.
Например, показатель рентабельности производства (R) определяется по формуле:
где П – сумма прибыли от реализации продукции; 3 – сумма затрат на производство и реализацию продукции.
Если сумму затрат разложить на отдельные элементы, то конечная модель будет иметь следующий вид:
Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, среднегодовую выработку продукции одним работником можно записать следующим образом:
Если ввести такой показатель, как количество отработанных дней всеми работниками (Добщ), то получим следующую модель годовой выработки:
где ДВ – среднедневная выработка; Д – количество отработанных дней одним работником.
Метод сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель.
Например, рентабельность операционного капитала рассчитывается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала предприятия (KL):
Если числитель и знаменатель полученного выражения разделить на выручку от реализации продукции (В), то получим кратную модель, но с новым набором факторов – рентабельности продаж и капиталоемкости продукции:
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде детерминированных моделей различных типов. Выбор способа моделирования зависит от объекта исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Источник
Формальное разложение
Метод формального разложения – удлинение знаменателя исходной модели путем замены одного или нескольких факторов суммой однородных показателей:

Расширение.
Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число. В результате получается конечная мультипликативная модель в виде произведения нового набора факторов:

Сокращение.
Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число. В результате получается конечная модель того же типа, что и исходная, но с другим набором факторов.

Процесс моделирования сложный и ответственный момент. От реальности и точности моделей зависят конечные результаты анализа.
Детализация в факторном анализе во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели.
ПРИМЕР:
Удельную себестоимость продукции можно представить в качестве функции двух факторов: суммарных затрат (TC) и объема выпуска продукции (Q). Исходная модель этой факторной системы будет иметь вид

1) преобразуйте общую сумму затрат (TC) с помощью одной из моделей, содержащей такие элементы, как оплата туда (ЗП), материальные затраты (МЗ), амортизация основных средств (А), накладные расходы (НР).
2) какая модель получилась в результатае?
1) если общую сумму затрат (TC) заменить отдельными их элементами, такими как оплата туда (ЗП), материальные затраты (МЗ), амортизация основных средств (А), накладные расходы (НР) и др., то получим аддитивную модель с набором новых факторов:

где x1 – трудоемкость продукции;
x2 – материалоемкость продукции;
x3 – фондоемкость продукции;
x4 – уровень накладных затрат.
2) модель – аддитивная.
Принципы построения многофакторных мультипликативных моделей
В основе построения многофакторных мультипликативных моделей лежат следующие принципы:
— место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;
— модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило, качественных, на составляющие;
— при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.
Источник





