Способ эксцентрических сфер когда применяется

Способ эксцентрических сфер когда применяется

Способ эксцентрических сфер основан на том, что около всякой окружности можно описать бесчисленное множество сфер, геометрическим местом центров которых является прямая, проходящая через центр окружности и перпендикулярная плоскости окружности. Этот способ применяется в следующих случаях:

• при определении линии пересечения поверхностей вращения со скрещивающимися осями;

• при определении линии пересечения поверхности вращения с поверхностью, имеющей круговые сечения.

В обоих случаях обязательным является наличие общей плоскости симметрии. Рассмотрим способ эксцентрических сфер на примере построения линии пересечения поверхностей конуса и кольца (рис. 113). Конус и кольцо имеют общую плоскость симметрии δ(δ₁), и их оси вращения i(i₁,i₂) и q(q₁,q₂ – скрещивающиеся прямые.

1. Определить опорные точки (рис. 114). Так как обе данные поверхности имеют общую плоскость симметрии δ(δ₁), параллельную плоскости проекций П₂, то их очерковые образующие, по отношению к плоскости П₂, пересекаются. Точки A(A₁,A₂) и B(B₁,B₂) пересечения этих образующих являются опорными точками.

Точка пересечения осей поверхностей принимается за центр вспомогательных концентрических сфер.

2. Для определения промежуточных точек в качестве вспомогательных поверхностей выбраны эксцентрические сферы, центры которых лежат на оси конуса.

Положение центров определяется следующим образом (рис. 115, 116): через ось кольца q(q₁,q₂) проводят плоскость σ(σ₂) ⊥ П₂ и заменяют «кривой цилиндр» (кольцо) соприкасающимся с ним по окружности прямым цилиндром (фронтальная проекция этого цилиндра показана на рис. 112 штрихпунктирными линиями). Ось этого цилиндра c ⊥ σ(c₂ ⊥ σ₂) и пересекает ось конуса в точке O:

Из точки O(O₂) проведена сфера такого радиуса r, чтобы она пересекала кольцо по окружности m(m₂).

Эта же сфера пересекает конус по окружности n (n₁,n₂). В пересечении окружностей m и n получаются точки C и D, принадлежащие искомой линии пересечения:

Чтобы построить горизонтальные проекции точек C и D, принадлежащих искомой линии пересечения, следует использовать окружность n (n₁,n₂) конической поверхности, так как она не искажается на плоскости проекций П₁:

3. Для определения точек E,F,G и H, принадлежащих искомой линии пересечения, проведены плоскости η(η₂) и μ(μ₂) (рис. 117). Центрами вспомогательных сфер являются точки O'(O’₂) и O»(O»₂) соответственно. Все остальные построения выполнены аналогичным образом.

4. Определить видимость очерковых образующих и линии пересечения поверхностей. На фронтальной проекции видимы будут те точки линии пересечения, которые лежат перед горизонтальной проекцией плоскости симметрии δ(δ₁), — точки A, G, C и B. На горизонтальной проекции поверхность конуса невидима, следовательно, невидима и вся линия пересечения. Искомая линия пересечения данных поверхностей u(u₁,u₂) приведена на рис. 117.

Рассмотрим также способ эксцентрических сфер на примере построения линии пересечения поверхности тора и наклонного (эллиптического) цилиндра (рис. 118).

В этом случае можно использовать способ эксцентрических сфер, так как одна из поверхностей является поверхностью вращения (тор), а другая (наклонный цилиндр) – поверхностью, имеющей круговые сечения, параллельные основанию цилиндра. Через любое круговое сечение можно провести бесконечное число сфер с центрами на перпендикуляре, восстановленном из центра кругового сечения. В данном случае центрами вспомогательных сфер будут точки пересечения оси вращения тора с перпендикулярами, восстановленными в центре произвольно выбранного кругового сечения цилиндра.

Причем обе поверхности имеют общую плоскость симметрии δ(δ₁), на которую круговые сечения поверхности цилиндра проецируются в виде отрезков прямых линий. Осями данных поверхностей являются прямые i(i₁,i₂) и q(q₁,q₂).

Алгоритм решения данной задачи состоит в следующем:

1. Сначала определяются опорные точки (рис. 119). Так как очерковые образующие обеих поверхностей лежат в одной плоскости – плоскости симметрии δ(δ₁), параллельной плоскости проекций П₂, точки A(A₁,A₂) и B(B₁,B₂) пересечения этих образующих являются опорными. .

2. Далее определяются промежуточные точки линии пересечения поверхностей (рис. 120). Порядок их определения сводится к следующему алгоритму:

2.1. Для определения кругового сечения поверхность цилиндра пересекается вспомогательной плоскостью β(β₂). Окружность d = β(β₂)∩ Ф kон – круговое сечение цилиндра.

2.2. Из точки L(L₂)=q₂ × β₂ , центра кругового сечения d(d₂), провести перпендикуляр до пересечения с осью i(i₁,i₂) тора. Точка O(O₂) является центром вспомогательной сферы.

2.3. Из точки O₂ радиусом, равным /O₂K₂/, построить окружность m(m₂) – фронтальную проекцию вспомогательной сферы. Затем определить линии пересечения вспомогательной сферы с данными поверхностями. С цилиндром сфера пересекается по окружности d(d₂), которая является его круговым сечением, а с поверхностью тора – по окружности l(l₁,l₂):

2.4. В пересечении окружностей d и l получаются точки C и D, принадлежащие искомой линии пересечения:

2.5. Чтобы построить горизонтальные проекции точек C и D, принадлежащих искомой линии пересечения, следует воспользоваться окружностью l(l₁,l₂) поверхности вращения, так как она не искажается на плоскости проекций П₁.

3. Аналогично определяются остальные точки линии пересечения поверхностей. Для определения точек E, F, G и H, принадлежащих искомой линии пересечения, проведены плоскости γ(γ₂) и η(η₂) (рис. 121). Пределы этих плоскостей по ширине определяют правая и левая опорные точки линии пересечения поверхностей – фронтальные проекции точек A и B. Центрами вспомогательных сфер являются точки O'(O’₂) и O»(O»₂) соответственно. Все остальные построения выполнены аналогичным образом.

4. В данном случае линия пересечения поверхностей цилиндра и тора представляет собой кривую второго порядка v(v₁,v₂) (см. рис. 121).

5. Точки S и P являются точками смены видимости. Их фронтальные проекции лежат на оси вращения цилиндра q(q₁,q₂), а горизонтальные проекции – на очерковых образующих цилиндра.

На фронтальной плоскости проекций видимы будут те точки линии пересечения, которые лежат перед горизонтальной проекцией очерковых образующих, проекции которых совпадают с плоскостью симметрии δ(δ₁), – точки A, G, S, E, С, B.

На горизонтальной плоскости проекций видимы точки P, H, A, G, S, фронтальные проекции которых лежат выше фронтальной проекции образующих, проекции которых совпадают с осью вращения цилиндра q(q₂).

Источник

Способ эксцентрических сфер когда применяется

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

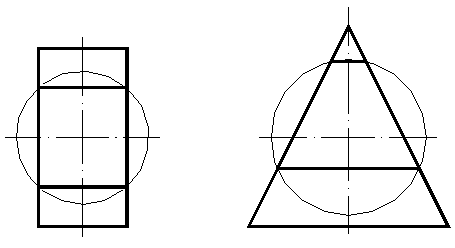
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей — прямые линии, а второй — когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

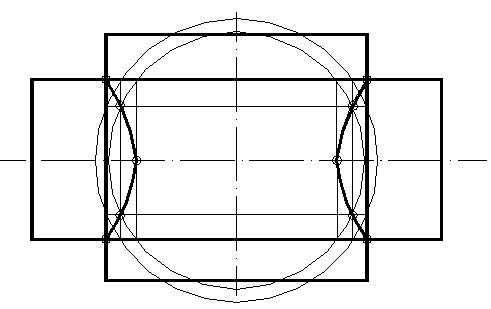
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

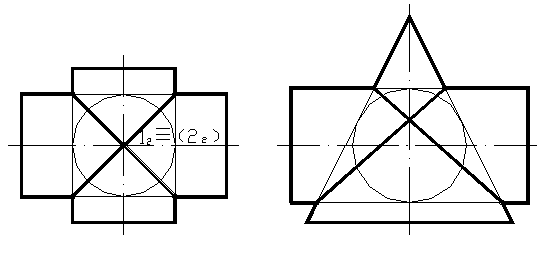
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

13.4. Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пе­ресекающиеся поверхности должны иметь семейство круговых сече­ний.

13.4.1 Задание: даны две поверхности вращения — тор и конус, оси которых находятся в одной плоскости, параллельной П₁ (рис. 13.7). Требуется построить линии их пересечения.

Решение: прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след ₂ фронтально проецирующей плоскости . Линия пересечения её с поверхностью тора — окруж­ность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомо­гательной секущей сферой по окружности, её центр должен находить­ся на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса (O₂) выбирается центром вспомогатель­ной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости 1.2- Такая вспомога­тельная секущая сфера пересекает кольцо и конус вращения по ок­ружностям, фронтальные проекции которых — отрезки прямых. Точка пресечения этих отрезков 3₂ (рис. 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции — точки 4₂ — О’₂. Горизон­тальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, кону­са.

Литература

Гордон В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. — М.: Высшая школа, 2000. — 272 с.

Гордон В.О. Сборник задач по курсу «Начертательная геомет­рия» / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева. — М.: Высшая школа,2000.

Чекмарев А.А. Инженерная графика. — М.: Высшая школа, 1998.-365с.

Фролов С.А. Начертательная геометрия. — М.: Высшая школа,1983.-240 с.

Арустамов Х.А. Сборник задач по начертательной геометрии. -М.: Машиностроение, 1978. -445 с.

Источник

Способ эксцентрических сфер когда применяется

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

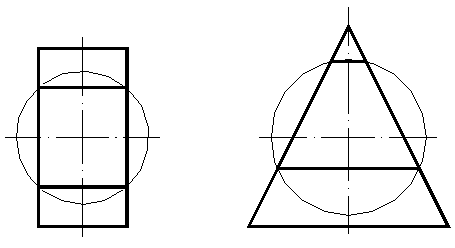
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей — прямые линии, а второй — когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

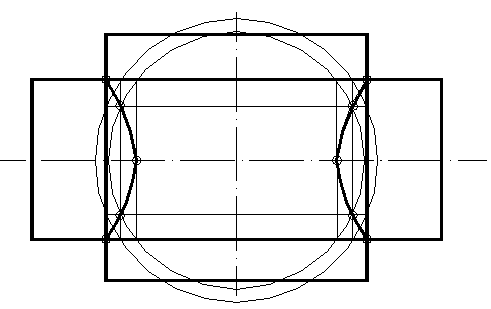
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

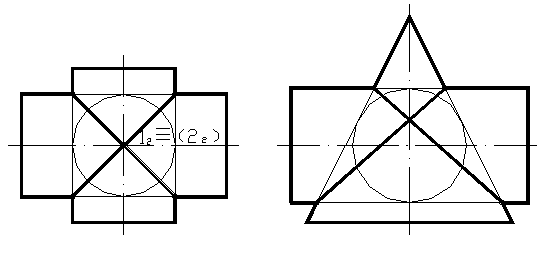
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник