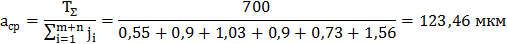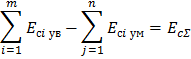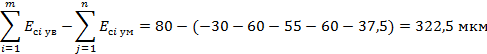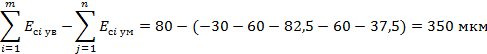Расчет размерных цепей
Прямая задача
Пример решения прямой задачи методом полной взаимозаменяемости
Способ равных квалитетов
Задание:
Рассчитать заданную размерную цепь (см. рис. 1) по методу полной взаимозаменяемости (max/min).
Допуски на составляющие звенья определять способом равных квалитетов (одного квалитета).
Сделать проверку выполненных расчетов.
Исходные данные:
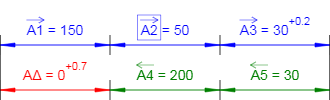
Рисунок 1 — Схема размерной цепи. Исходные данные.
Звенья размерной цепи:
A1 = 150 (мм)
A2 = 50 (мм)
A3 = 30 +0,2 (мм) — звено с известным допуском;
A4 = 200 (мм)
A5 = 30 (мм)
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5;
Компенсирующее звено: A2
Замыкающее звено: AΔ
Верхнее отклонение замыкающего звена Es(AΔ) = 0,7 мм
Нижнее отклонение замыкающего звена: Ei(AΔ) = 0 мм
Решение:
1. Определение характеристик замыкающего звена.
1.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
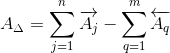 | (1) |
Тогда для заданной размерной цепи формула (1) принимает вид:
AΔ = A1 + A2 + A3 — (A4 + A5)
AΔ = 150 + 50 + 30 — (200 + 30) = 0(мм)
1.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
| T(A Δ ) = Es(A Δ ) — Ei(A Δ ) | (2) |
тогда
T(AΔ) = 0,7 — 0 = 0,7(мм)
2. Определение характеристик составляющих звеньев размерной цепи.
2.1. Определение допусков составляющих звеньев
2.1.1 Определение значений единиц допуска составляющих звеньев.
По таблице 1 принимаем количество единиц допуска для каждого звена.
Таблица 1 — Значение единиц допуска i для различных интервалов размеров.
| Интервалы размеров, мм | 1-3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i, мкм | 0,55 | 0,73 | 0,90 | 1,08 | 1,31 | 1,56 | 1,86 | 2,17 | 2,52 | 2,90 | 3,23 | 3,54 |
2.1.2 Определение числа единиц допуска.
Число единиц допуска «а» находим по формуле:
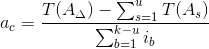 | (3) |
Тогда для заданной размерной цепи формула (3) принимает вид:
| аc = | T(AΔ) — T(A3) |
| i1 + i2 + i4 + i5 |
тогда
| аc = | 700 — 200 | = 60,4 |
| 2,52 + 1,56 + 2,89 + 1,31 |
2.1.3 Определение квалитетов составляющих звеньев.
По числу единиц допуска аc=60,4 принимаем квалитет 9 (см. табл.2).
Таблица 2 — Число единиц допуска, содержащихся в допуске по квалитетам, коэффициент точности «а».
| Квалитет IT | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэф. точн. а | 7 | 10 | 16 | 25 | 40 | 64 | 100 | 160 | 250 | 400 | 640 | 1000 |
На составляющие звенья назначаем допуски по 9 квалитету (см. табл.3).
На увеличивающие размеры допуски назначаем по H
На уменьшающие размеры допуски назначаем по h
Таблица 3 — Величины допусков (мкм) для различных интервалов размеров (мм) и квалитетов
| Квалитеты | Интервалы (свыше) – до, мм | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| До 3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 | 400-500 | |
| 5 | 4 | 5 | 6 | 8 | 9 | 11 | 13 | 15 | 18 | 20 | 23 | 25 | 27 |
| 6 | 6 | 8 | 9 | 11 | 13 | 16 | 19 | 22 | 25 | 29 | 32 | 36 | 40 |
| 7 | 10 | 12 | 15 | 18 | 21 | 25 | 30 | 35 | 40 | 46 | 52 | 57 | 63 |
| 8 | 14 | 18 | 22 | 27 | 33 | 39 | 46 | 54 | 63 | 72 | 81 | 89 | 97 |
| 9 | 25 | 30 | 36 | 43 | 52 | 62 | 74 | 87 | 100 | 115 | 130 | 140 | 155 |
| 10 | 40 | 48 | 58 | 70 | 84 | 100 | 120 | 140 | 160 | 185 | 210 | 230 | 250 |
| 11 | 60 | 75 | 90 | 110 | 130 | 160 | 190 | 220 | 250 | 290 | 320 | 360 | 400 |
| 12 | 100 | 120 | 150 | 180 | 210 | 250 | 300 | 350 | 400 | 460 | 520 | 570 | 630 |
| 13 | 140 | 180 | 220 | 270 | 330 | 390 | 460 | 540 | 630 | 720 | 810 | 890 | 970 |
| 14 | 250 | 300 | 360 | 430 | 520 | 620 | 740 | 870 | 1000 | 1150 | 1300 | 1400 | 1550 |
| 15 | 400 | 480 | 580 | 700 | 840 | 1000 | 1200 | 1400 | 1600 | 1850 | 2100 | 2300 | 2500 |
| 16 | 600 | 750 | 900 | 1100 | 1300 | 1600 | 1900 | 2200 | 2500 | 2900 | 3200 | 3600 | 4000 |
2.3. Определение середины поля допуска i-го звена
Середину поля допуска i-го звена определим по формуле:
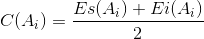 | (4) |
тогда
| С(A1) = | (0,1 + 0) | = 0,05 |
| 2 |
| С(A3) = | (0,2 + 0) | = 0,1 |
| 2 |
| С(A4) = | (0 + (-0,115)) | = -0,0575 |
| 2 |
| С(A5) = | (0 + (-0,052)) | = -0,026 |
| 2 |
3. Определение характеристик компенсирующего звена.
Компенсирующее звено: A2 — увеличивающее звено
3.1. Определение допуска компенсирующего звена.
Допуск компенсирующего звена определим по формуле:
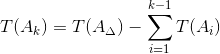 | (5) |
Тогда для заданной размерной цепи формула (5) принимает вид:
T(A2к) = T(AΔ) — (T(A1) + T(A3) + T(A4) + T(A5))
тогда
TA2к = 0,7 — (0,1 + 0,2 + 0,115 + 0,052) = 0,233 (мм)
3.2. Определение середины поля допуска компенсирующего звена
Середину поля допуска компенсирующего звена определим по формуле:
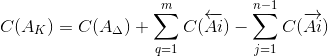 | (6) |
Тогда для заданной размерной цепи формула (6) принимает вид:
C(A2к) = C(AΔ) + (C(A4) + C(A5)) — (C(A1) + C(A3))
тогда
С(A2к) = 0,35 + ((-0,0575) + (-0,026)) — (0,05 + 0,1) = 0,1165
3.3. Определение верхнего отклонения компенсирующего звена
Верхнее отклонение компенсирующего звена определим по формуле:
| Es(Ak ) = C(Ak ) + 0,5⋅T(k ) | (7) |
тогда
Es(Aк) = 0,1165 + (0,5⋅0,233) = 0,233
3.4. Определение нижнего отклонения компенсирующего звена
Нижнее отклонение компенсирующего звена определим по формуле:
| Ei(Ak ) = C(Ak ) — 0,5⋅T(k ) | (8) |
тогда
Ei(Aк) = 0,1165 — (0,5⋅0,233) = 0
Звенья размерной цепи с определенными допусками:
A1 = 150H9 (+0,1) (мм);
A2 = 50 +0,233 (мм);
A3 = 30 +0,2 (мм);
A4 = 200h9(-0,115) (мм);
A5 = 30h9(-0,052) (мм);
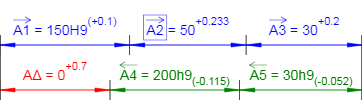
Рисунок 2 — Схема размерной цепи. Результаты расчета.
Проверка правильности решения задачи производится по формулам:
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
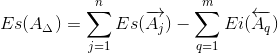 | (9) |
Тогда для заданной размерной цепи формула (9) принимает вид:
Es(AΔ) = Es(A1) + Es(A2) + Es(A3) — (Ei(A4) + Ei(A5))
тогда
Es(AΔ) = 0,1 + 0,233 + 0,2 — ((-0,115) + (-0,052)) = 0,7
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
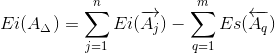 | (10) |
Тогда для заданной размерной цепи формула (10) принимает вид:
Ei(AΔ) = Ei(A1) + Ei(A2) + Ei(A3) — (Es(A4) + Es(A5))
тогда
Ei(AΔ) = 0 + 0 + 0 — (0 + 0) = 0
Источник
Способ одного квалитета
Рассчитаем сборочную размерную цепь методом максимума-минимума, способом одного квалитета. Все исходные данные для расчета сохраняются.
По табл. 1 определяем значения единиц допуска для составляющих звеньев:
Среднее число единиц допуска
Выбираем ближайший 11-й квалитет по таблице 1 со стандартным числом единиц допуска а = 100 и по этому квалитету определяем допуски составляющих звеньев (допуски на кольца подшипников определяются по табл.2 в зависимости от класса точности).
Т 1 = 60 мкм; Т 2 = 120 мкм;
Т 3 = 110 мкм; Т 4 = 120 мкм;
Т 5 = 75 мкм; Т 6 = 160 мкм;
Проверим условие (2):
∑ Т i = 60+120+110+120+75+160=645 мкм
Сумма допусков составляющих звеньев составляет 645 мкм, следовательно условие (2) выполняется.
По выбранным допускам звеньев размерной цепи определяем средние отклонения звеньев. При этом для увеличивающих звеньев, как для охватывающих, поля допусков определяются как для основных отверстий, а для уменьшающих звеньев, как для охватываемых, — как для основных валов. Это правило не относится к подшипникам качения.
Проверяем условие по средним отклонениям
| (3) |
Где 
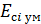
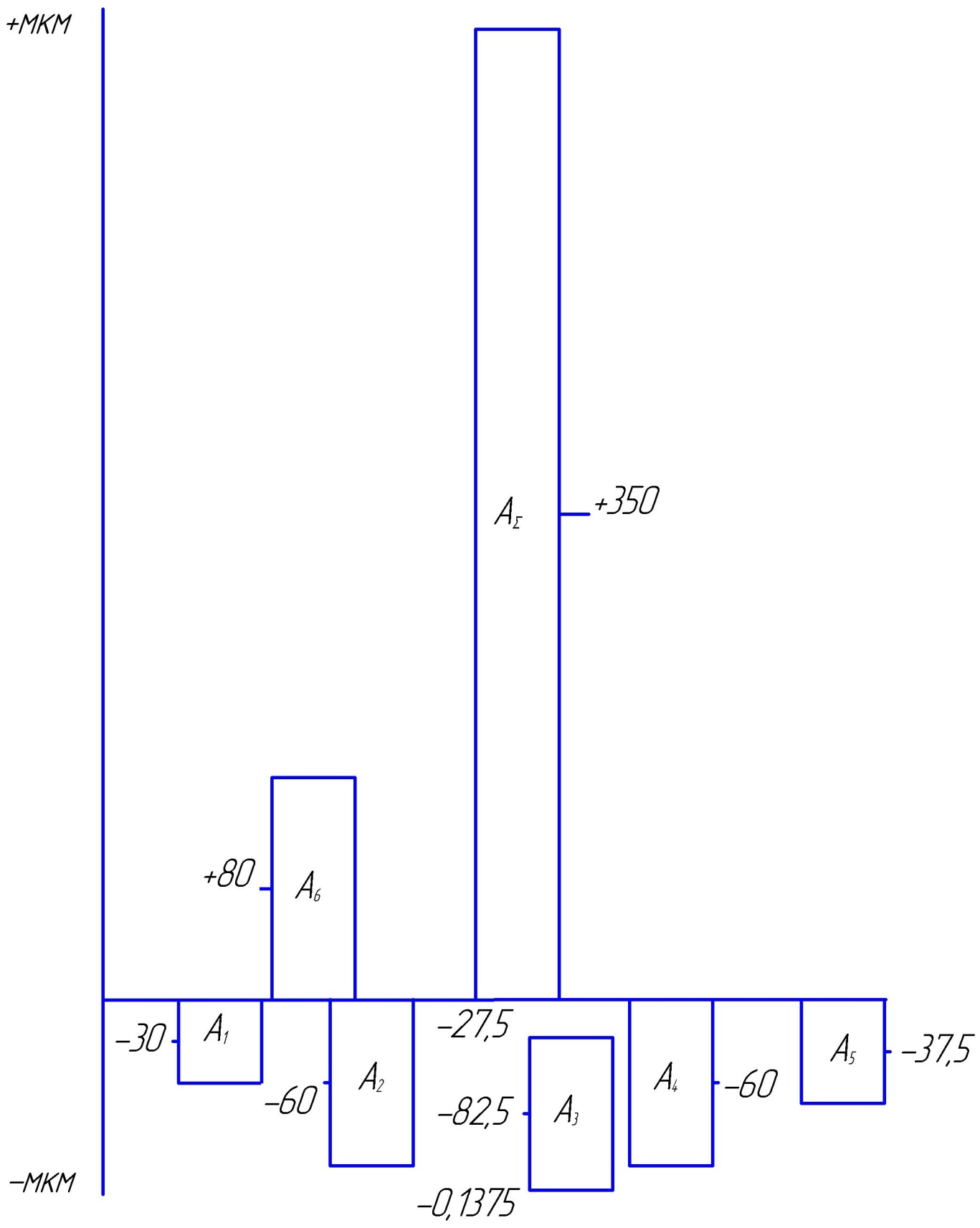
Условие не выполняется. При Ес∑ = 350мкм условие выполняется.
Выбираем зависимое звено для корректировки его среднего отклонения. В качестве зависимого звена выбираем такое, которое является наиболее технологичным, т.е. самым простым для обеспечения при изготовлении детали необходимых предельных отклонений. Таким звеном в нашем примере является А3.
Рис. 1. Схема полей допусков составляющих звеньев
и средних отклонений
Для выполнения условия необходимо, чтобы Ес3 = -82,5 мкм.
Проверяем условие (3):
т.е. условие по средним отклонениям выполняется.
Тогда А1 = 2-0,060 ; А3 = 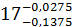
На этом расчет размерной цепи методом максимума-минимума, способом одного квалитета закончен.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник