Способ доказательства по схеме

Доказательства тех или иных утверждений в математике строятся на основании определенных правил, сущность которых выражают тавтологические импликации логики высказываний. Они схематично отражают шаги построения доказательств, поэтому их называют схемами или правилами доказательств (см., например, ниже правило заключения, правило контрапозиции и т. д.). Приведем правила, которые соответствуют первым 15 тавтологическим импликациям теоремы 1.3:

Часто при записи этих правил помещают посылки над горизонтальной линией, а заключение — под ней.

При такой записи приведенные выше схемы доказательств принимает вид:

Косвенное доказательство (доказательство от противного). Совокупность формул логики высказываний называется противоречивой, если при любом распределении истинностных значений входящих в них атомов хотя бы одна из формул получает значение A. Легко видеть, что совокупность формул противоречива тогда и только тогда, когда формула есть противоречие, т. е. является тождественно ложной формулой.

ТЕОРЕМА 2.5. Если из совокупности формул логически следует противоречие, то эта совокупность формул противоречива.

Доказательство. Предположим,что , где F — тождественно ложная формула. Тогда по теореме 2.3

В силу таблицы истинности для импликации отсюда следует, что формула тождественно ложна. Следовательно, совокупность формул противоречива.

Тождественно ложные формулы (противоречия) играют существенную роль в методе косвенного доказательства, называемого также методом доказательства от противного. Основой такого рода доказательств является следующая теорема.

ТЕОРЕМА 2.6. Если из формул логически следует противоречие, то

Доказательство. Предположим, что где F — противоречие. Тогда по теореме 2.5 совокупность формул противоречива. Поэтому если для какого-либо распределения истинностных значений атомов, входящих в формулы все формулы получают значение И, то формула получает значение A, а значит, В получает значение И. Следовательно,

Таким образом, если нужно доказать, что некоторое высказывание В логически следует из данных посылок, мы присоединяем к этим посылкам и показываем, что из посылок следует противоречие (обычно оно имеет вид ). После этого можно заключить, что высказывание В есть логическое следствие исходных посылок. Частным является случай, когда т. е. не задаются никакие посылки. Если, допустив истинность , выведем противоречие , то можем утверждать истинность В. Это рассуждение основывается на правиле доказательства, от противного: .

Очень распространенным является способ доказательства разбором случаев, который заключается в следующем. Пусть требуется доказать истинность высказывания С.

Строим высказывания А и В такие, что — истинные высказывания (часто в качестве В берут отрицание А). Тогда на основании соответствующей схемы доказательства можно утверждать истинность С.

На основании правила силлогизма можно утверждать истинность высказывания если можно построить такую цепочку импликаций

каждая из которых истинна.

1. Обоснуйте следующие схемы доказательств:

2. Докажите, что для любой формулы логики высказываний существует логически эквивалентная формула, построенная только с помощью одной из следующих пар связок:

Источник

§ 3. Виды доказательства

§ 3. Виды доказательства

Доказательные рассуждения различаются, прежде всего, по своему отношению к выдвинутому тезису. В результате этого можно или подтверждать истинность тезиса, или опровергать, доказывая его ложность.

Целенаправленность демонстрации служит исходным основанием для деления всех доказательств. Она предопределяет все построение и характер дальнейшего рассуждения.

Цель эта определяется не произвольно, а в зависимости от содержания обосновываемого положения. Невозможно подтвердить тезис, который не соответствует действительности, нельзя также опровергнуть истинный тезис.

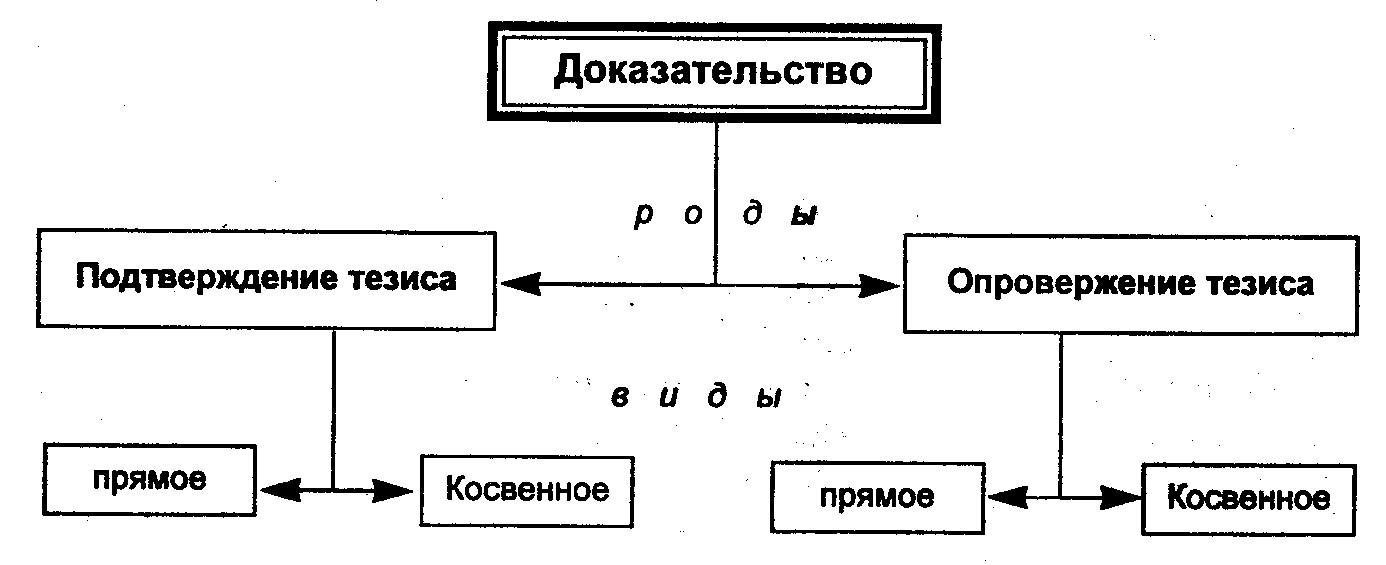
Отсюда различают два рода доказательств:

1) подтверждение тезиса;

2) опровержение тезиса.

По способу аргументации все доказательства делятся на два вида: а) прямые и б) косвенные.

Прямое доказательство заключается в непосредственном выведении из основания по определенным правилам умозаключения истинности или ложности данного тезиса.

Косвенное доказательство заключается в обосновании ложности или истинности положения, находящегося в определенном отношении с тезисом, и отсюда опосредованно устанавливается истинность тезиса или, наоборот, его ложность.

Для наглядности представим приведенные рассуждения в виде схемы:

Рассмотрим каждый вид доказательства более подробно.

Прямым подтверждением тезиса называется доказательство, в котором истинность тезиса обосновывается непосредственно аргументами. Например, для доказательства тезиса «Для всех преступлений против личной собственности граждан Уголовным кодексом Российской Федерации предусмотрено в качестве санкции лишение свободы» можно привести следующие аргументы:

— во-первых, преступления против личной собственности граждан предусмотрены в восьми статьях Уголовного кодекса России: кража, грабеж, разбой, мошенничество и т.д.;

— во-вторых, для каждого из восьми преступлений в качестве санкции предусмотрено лишение свободы.

Поскольку аргументы исчерпывают все разновидности преступлений против личной собственности граждан, то обоснование строится в форме умозаключения полной индукции, в котором из истинных посылок с необходимостью следует истинность заключения. Это — прямое подтверждение выдвинутого тезиса. Оно осуществляется в два этапа: подыскиваются подходящие аргументы, и затем демонстрируется, что из них логически вытекает тезис.

Прямое подтверждение тезиса осуществляется следующими методами:

— дедуктивное подтверждение тезиса. Его сущность состоит в выведении тезиса из установленной истинности аргументов, в подведении частного случая под общее правило;

— индуктивное подтверждение тезиса. Достигается через полную индукцию, путем исчерпывания всех возможных случаев истинности доказываемого тезиса и обобщения их в едином выводе.

Таким образом, при прямом подтверждении тезиса задача состоит в том, чтобы найти убедительные аргументы, из которых логически вытекает данный тезис.

Косвенным подтверждением тезиса называется такое доказательство, которое устанавливает истинность доказываемого тезиса, исследуя не сам тезис, а некоторые другие положения, находящиеся с ним в определенных логических отношениях. Эти положения так связаны с доказываемым тезисом, что из установления их ложности необходимо вытекает истинность доказываемого тезиса.

Косвенное подтверждение тезиса осуществляется двумя методами:

— апагогическое подтверждение тезиса, при котором к его истинности приходят путем обоснования ложности антитезиса. Антитезисом называется суждение, противоречащее тезису.

Апагогическое подтверждение тезиса проходит следующие этапы: выдвигается антитезис и из него выводятся следствия с намерением найти среди них хотя бы одно ложное; устанавливается, что в числе следствий действительно есть ложное; делается вывод, что антитезис неверен; из ложности антитезиса на основании закона исключенного третьего делается заключение, что выдвинутый тезис является истинным.

Косвенное апагогическое подтверждение тезиса называют еще сведением к абсурду.

Апагогическое подтверждение тезиса довольно часто используется в судебном доказывании. Оно имеет здесь исключительное значение в тех случаях, когда по поводу какого-либо обстоятельства можно выдвинуть только две противоречащих версии. Обоснование ложности одной из них (антитезиса) в таких случаях является убедительным доказательством истинности другой версии;

— разделительное подтверждение тезиса. Его сущность состоит в том, что доказываемый тезис рассматривается как одно из некоторого числа предположений, в своей сумме исчерпывающих все возможные по данному вопросу предположения.

Разделительное подтверждение тезиса применяется в тех случаях, когда можно быть уверенным, что доказываемое положение входит в число всех рассматриваемых возможностей. В качестве иллюстрации рассмотрим следующий пример. В одной из экспедиций, в которой участвовало пять человек, было совершено преступление: пропал дорогой прибор. Ознакомившись с обстоятельствами дела, следователь установил, что преступление мог совершить кто-либо из членов экспедиции, так как кроме этих лиц никого другого не было на острове, где проходили работы. Начальник экспедиции, его помощник, инженер, врач, как стало известно в ходе следственных действий, не совершали преступления; было доказано, что преступление совершил проводник.

Косвенное подтверждение тезиса этим способом ведется так: одна за другой исключаются все альтернативы, кроме одной, которая и является доказываемым тезисом. В апагогическом подтверждении тезиса альтернативы (тезис и антитезис) исключают друг друга в силу законов логики. В разделительном же подтверждении тезиса взаимная несовместимость возможностей и то, что ими исчерпываются все мыслимые ситуации, определяются не логическими, а фактическими обстоятельствами. Отсюда понятна обычная ошибка при разделительном подтверждении тезиса: выдвинутые возможности, вместе взятые, не исчерпывают всех возможных альтернатив.

Косвенное подтверждение тезиса представляет собой эффективное средство обоснования выдвигаемых положений. Однако его специфика в определенной мере ограничивает использование в мыслительной деятельности юриста. Имея дело с этим доказательством, мы все время вынуждены сосредоточивать свое внимание не на тезисе, истинность которого следует обосновать, а на отрицании других положений, являющихся ошибочными предположениями. Неудивительно поэтому, что после того, как такое доказательство проведено, ход его иногда рекомендуют тут же забыть, оставив в памяти только подтвержденный тезис. Необходимо отметить, что найденное подтверждение какого-то положения, как правило, удается перестроить в прямое подтверждение этого же положения:

Подтверждению тезиса в доказательстве противостоит его опровержение. Опровержением называется доказательство ложности какого-либо тезиса. Опровержение отличается от подтверждения своим отношением к выдвинутому тезису. Поэтому опровержение является как бы зеркальным отображением подтверждения тезиса. Избегая повтора, ограничимся анализом методов основных видов опровержения.

1. Прямое опровержение тезиса:

а) опровержение тезиса путем лишения основания. Это достигается:

— разрушением выставленного основания фактами, новыми положениями, законами науки (фактическое лишение основания);

— через демонстрацию отсутствия необходимой связи между данным тезисом и выдвинутым основанием (логическое лишение основания). Успешное использование данного способа опровержения предполагает четкое представление о правилах и ошибках соответствующих умозаключений — дедукции, индукции или аналогии, в форме которых протекает обоснование тезиса;

б) опровержение тезиса через опровержение вывода. Это достигается в соответствии с логическим правилом отрицающего модуса условно-категорического умозаключения, когда рассуждение направлено от отрицания следствия к отрицанию основания.

2. Косвенное опровержение тезиса:

а) апагогическое опровержение тезиса. Выдвигается антитезис и доказывается любым из методов подтверждения его истинность. Тезис, таким образом, опровергается косвенным путем через подтверждение антитезиса;

б) разделительное опровержение тезиса. Оно строится по схеме:

либо А, либо В, либо С есть Р

___________А есть Р___________

Следовательно, ни В, ни С не есть Р

Рассмотренные методы основных видов опровержения тезиса применяются не только самостоятельно, но и в сочетании друг с другом.

Убеждающая сила рассуждения во многом определяется также рациональным сочетанием подтверждения и опровержения, способствующим достижению в каждом конкретном случае несомненных, объективно-истинных результатов. При этом будущим юристам необходимо иметь в виду, что деление доказательств на прямые и косвенные в логике не совпадает с делением доказательств на прямые и косвенные в уголовном процессе. Совпадает здесь только терминология.

В логике, как уже отмечено, под доказательством понимается мыслительный процесс обоснования истины, в уголовном же процессе доказательство — это доказательственный факт, факт действительности. Поэтому предмет деления в логике и уголовном процессе разный. В уголовном процессе на прямые и косвенные делятся факты действительности (доказательственные факты) и средства доказывания (источники доказательств). Основанием деления доказательственных фактов на прямые и косвенные является здесь их связь с искомым фактом.

Прямыми доказательствами в уголовном процессе являются такие факты, которые связаны с искомым фактом (доказываемым положением) непосредственно. Связь прямого доказательства с искомым фактом очевидна.

Косвенное доказательство — это такие факты, связь которых с искомым фактом (доказываемым положением) не дана нам непосредственно, не является очевидной.

С целью получения более глубоких знаний о практическом использовании логического доказательства будущим правоведам полезно проанализировать речи, произнесенные во время судебных процессов видными юристами[13].

Способ доказательства по схеме