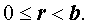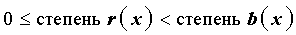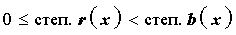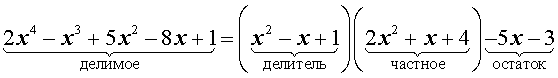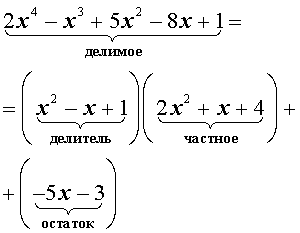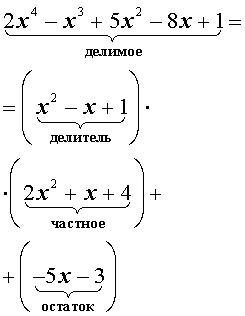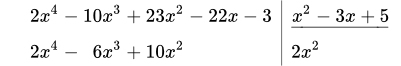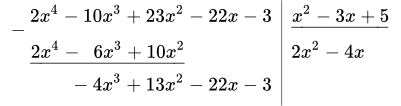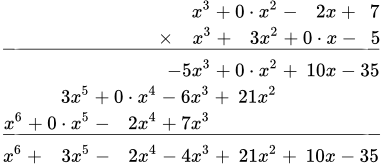Способ деления многочленов углом

Деление многочленов уголком

Сегодня мы узнаем, как выполняется деление многочленов друг на друга, причем выполнять деление мы будем уголком по аналогии с обычными числами. Это очень полезный прием, который, к сожалению, не изучают в большинстве школ. Поэтому внимательно прослушайте данный видеоурок. Ничего сложного в таком делении нет.

Для начала давайте разделим друг на друга два числа:

Как можно это сделать? В первую очередь, мы отсекаем столько разрядов, чтобы полученное числовое значение было больше чем то, на которое мы делим. Если мы отсечем один разряд, то получим пять. Очевидно, семнадцать в пять не вмещается, поэтому этого недостаточно. Берем два разряда — у нас выйдет 59 — оно уже больше, чем семнадцать, поэтому мы можем выполнить операцию. Итак, сколько раз семнадцать помещается в 59? Давайте возьмем три. Перемножаем и записываем результат под 59. Итого у нас получилось 51. Вычитаем и у нас вышло «восемь». Теперь сносим следующий разряд — пять. Делим 85 на семнадцать. Берем пять. Перемножим семнадцать на пять и получаем 85. Вычитаем и у нас получается ноль.

Решаем реальные примеры

Задача № 1

Теперь выполним те же самые шаги, но не с числами, а с многочленами. Для примера возьмем такое:

Обратите внимание, если при делении чисел друг на друга мы подразумевали, что делимое всегда больше делителя, то в случае деления полиномов уголком, необходимо, чтобы степень делимого была больше, чем делителя. В нашем случае все в порядке — мы работаем с конструкциями второй и первой степени.

Итак, первый шаг: сравниваем первые элементы. Вопрос: на что нужно домножить $x$, чтобы получилось $<^<2>>$? Очевидно, что на еще один $x$. Умножаем $x+5$ на только что найденное число $x$. У нас есть $<^<2>>+5$, которое вычитаем из делимого. Остается $3x$. Теперь сносим следующее слагаемое — пятнадцать. Снова посмотрим на первые элементы: $3x$ и $x$. На что следует домножить $x$, чтобы вышло$3x$? Очевидно, что на три. Домножаем почленно $x+5$ на три. Когда мы вычтем, то получим ноль.

Как видите, вся операция деления уголком свелась к сравнению старших коэффициентов при делимом и делителе. Это даже проще, чем когда вы делите числа. Тут не требуется выделять какое-то количество разрядов — мы просто на каждом шаге сравниваем старшие элементы. Вот и весь алгоритм.

Задача № 2

Давайте попробуем еще:

Первый шаг: посмотрим на старшие коэффициенты. На сколько нужно домножить $x$, чтобы записать$<^<2>>$? Домножаем почленно. Обратите внимание, при вычитании у нас получится именно $2x$, потому что

Сносим -2 и снова сравним первый полученный коэффициент со старшим элементом делителя. Итого у нас вышел «красивый» ответ.

Переходим ко второму примеру:

В этот раз в качестве делимого выступает полином третьей степени. Сравним между собой первые элементы. Для того чтобы получилось $<^<3>>$, необходимо $x$ домножить на $<^<2>>$. После вычитания сносим $9x$. Домножаем делитель на $-x$ и вычитаем. В итоге наше выражение полностью разделилось. Записываем ответ.

Задача № 3

Переходим к последней задаче:

Сравниваем $<^<3>>$ и $x$. Очевидно, нужно домножить на $<^<2>>$. В итоге мы видим, что мы получили очень «красивый» ответ. Записываем его.

Вот и весь алгоритм. Ключевых моментов здесь два:

1. Всегда сравнивайте первую степень делимого и делителя — повторяем это на каждом шаге;
2. Если в исходном выражении пропущены какие-либо степени, при делении уголком их обязательно следует добавить, но с нулевыми коэффициентами, иначе ответ будет неправильным.

Больше никаких премудростей и хитростей в таком делении нет.

Краткое содержание

Материал сегодняшнего урока нигде и никогда не встречается в «чистом» виде. Его редко изучают в школах. Однако умение делить многочлены друг на друга очень поможет вам при решении уравнений высших степеней, а также всевозможных задач «повышенной трудности». Без данного приема вам придется раскладывать многочлены на множители, подбирать коэффициенты — и результат при этом отнюдь не гарантирован. Однако многочлены можно делить и уголком — так же, как и обычные числа! К сожалению, данный прием не изучают в школах. Многие учителя считают, что деление многочленов уголком — это что-то безумно сложное, из области высшей математики. Спешу вас заверить: это не так. Более того, делить многочлены даже проще, чем обычные числа! Посмотрите урок — и убедитесь в этом сами.:) В общем, обязательно возьмите этот прием на вооружение. Умение делить многочлены друг на друга очень пригодится вам при решении уравнений высших степеней и в других нестандартных задачах.

Я надеюсь, этот ролик поможет тем, кто работает с полиномами, особенно высших степеней. Это относится и к старшеклассникам, и к студентам университетов. А у меня на этом все. До встречи!

Источник

Деление многочлена на многочлен «уголком»

В этой статье рассмотрим один из способов разложения на множители многочленов высших степеней. С его помощью вы сможете решать уравнения и неравенства вида:

Пример:
\(6x^2+6+x^3+11x\) записываем как \(x^3+6x^2+11x+6\)

1) Подбором найдите один из корней многочлена.

Для этого вместо \(x\) подставьте по очереди числа: \(±1,±2,±3,±4,±5\) и т.д. Число, которое сделает многочлен нулем и будет его корнем.

Пример:
\(x^3+6x^2+11x+6\)
Подставим \(1\). Имеем: \(1^3+6 \cdot 1^2+11\cdot 1+6=24\) — не равно нулю. Ищем дальше.
Подставим \(-1\). Получим: \((-1)^3+6\cdot (-1)^2+11\cdot (-1)+6=-1+6-11+6=0\) – значит \(-1\) корень нашего многочлена.

Матхак! Пробуйте сначала числа, на которые свободный член делиться нацело. В данном случае свободный член \(6\), поэтому в первую очередь нужно пробовать числа: \(±1,±2,±3\) и \(±6\).

2) Поделите исходный многочлен на \(x-x_0\), где \(x_0\) – найденный корень. Процесс деления многочлена на многочлен сильно похож на обычное деление в столбик — поэтому и называется деление «уголком».

а) Запишите многочлены как числа при делении столбиком:

б) Подберите такой одночлен, чтобы при умножении его на \(x\), получалось первое слагаемое исходного многочлена, то есть в нашем случае \(x^3\). Очевидно, что таким одночленом будет \(x^2\).

в) Умножьте этот одночлен на делитель и запишите результат под исходным многочленом. Таким образом, мы умножаем \(x^2\) на \(x+1\) и получаем \(x^3+x^2\).

г) Теперь точно так же, как в случае деления натуральных чисел, поставьте знак минус, проведите горизонтальную черту и сделайте вычитание.

д) Повторите шаги б) – г) только уже с новым многочленом:
— подберите такой одночлен, чтобы при умножении на \(x\) первое слагаемое было таким же, как в новом многочлене: в нашем примере этим одночленом будет \(5x\).
— умножьте этот одночлен на делитель: умножив \(5x\) на \(x+1\) получим \(5x^2+5x\).
— вычтите получившиеся многочлены:

е) И вновь повторяем шаги б) – г) до тех пор, пока после вычитания не останется ноль.

3) Запишите новый вид многочлена, представив его как произведение делителя и частного.
\(x^3+6x^2+11x+6=(x+1)(x^2+5x+6)\)

Матхак! Если есть сомнения в правильности разложения, можно проверить его раскрытием скобок – в результате должен получиться исходный многочлен.
Проверим наш случай: \((x+1)(x^2+5x+6)=x^3+5x^2+6x+x^2+5x+6=x^3+6x^2+11x+6\).
Получен исходный многочлен, значит, поделили правильно.

Матхак! Если в результате деления у вас в остатке получился не ноль, значит, скорее всего, в решении есть ошибка.

Давайте теперь решим пример с применением изученного материала.

Пример: Решите неравенство \(x^4-3x^3+6x-4≥0\).

Найдем один из корней многочлена слева. Проверим \(1\).

Поделим многочлен \(x^4-3x^3+6x-4\) на \((x-1)\) уголком. Однако замечаем, что у нас нет слагаемого с квадратом. Чтоб нам было удобнее решать, запишем вместо него выражение \(0·x^2\) (ведь его значение равно нулю, а значит оно ничего не меняет в исходном многочлене).

Запишем новый вид нашего неравенства.

С первой скобкой все хорошо, а вот вторую надо бы разложить еще. Так как высшая степень в ней — куб, то мы можем попробовать разложить методом группировки, что проще чем деление в столбик. У первых двух слагаемых вынесем за скобку \(x^2\), а у третьего и четвертого – минус двойку.

Теперь выносим общую скобку \((x-2)\) за скобку.

Но и это еще не все, потому что \(x^2-2\) можно разложить с помощью формулы сокращенного умножения «разность квадратов»: \(a^2-b^2=(a-b)(a+b)\).

Вот сейчас все готово для применения метода интервалов .

Источник

Алгоритм деления «уголком» многочленов от одной переменной

Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:

где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:

Если друг на друга делить многочлены, то возникает похожая ситуация.

Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

Однако в результате деления многочленов многочлен получается далеко не всегда.

Говорят, что один многочлен нацело (без остатка) делится на другой многочлен , если результатом деления является многочлен.

Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком , в результате которого и частное, и остаток будут многочленами.

Определение . Разделить многочлен a(x) на многочлен b(x) с остатком – это значит представить многочлен a(x) в виде

где многочлен c(x) – частное , а многочлен r(x) – остаток , причем, степень остатка удовлетворяет неравенству:

Очень важно отметить, что формула

является тождеством, т.е. равенством, справедливым при всех значениях переменной x .

При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

Один из способов деления многочленов с остатком – это деление многочленов «уголком» , что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

К описанию этого способа деления многочленов мы сейчас и переходим.

Пример . Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

Решение . Опишем алгоритм деления многочленов «уголком» по шагам:

Делим первый член делимого 2x 4 на первый член делителяx 2 . Получаем первый член частного 2x 2 .

Умножаем первый член частного 2x 2 наделительx 2 – x + 1, а результат умножения

пишем под делимым 2x 4 – x 3 + 5x 2 – 8x + 1 .

Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток

Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член остаткаx 3 на первый член делителяx 2 . Получаем второй член частного x .

Умножаем второй член частного x на делительx 2 – x + 1 , а результат умножения

пишем под первым остатком x 3 + 3x 2 – 8x .

Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член второго остатка 4x 2 на первый член делителяx 2 . Получаем третий член частного 4 .

Умножаем третий член частного 4 на делительx 2 – x + 1 , а результат умножения

пишем под вторым остатком.

Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток

Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен.

Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:

Источник

Деление и умножение многочленов уголком и столбиком

Теорема

Пусть P_k ( x ) , Q_n ( x ) – многочлены от переменной x степеней k и n , соответственно, причем k ≥ n . Тогда многочлен P_k ( x ) можно представить единственным способом в следующем виде:
(1) P_k ( x ) = S_k–n ( x ) Q_n ( x ) + U_{n– 1} ( x ) ,
где S_k–n ( x ) – многочлен степени k–n , U_{n– 1} ( x ) – многочлен степени не выше n– 1 , или нуль.

Доказательство

По определению многочлена:
;
;
;
,
где p_i , q_i – известные коэффициенты, s_i , u_i – неизвестные коэффициенты.

Введем обозначение:
.
Подставим в (1) :
;
(2) .
Первый член в правой части – это многочлен степени k . Сумма второго и третьего членов – это многочлен степени не выше k – 1 . Приравняем коэффициенты при x k :
p_k = s_k-n q_n .
Отсюда s_k-n = p_k / q_n .

Преобразуем уравнение (2):
.
Введем обозначение: .
Поскольку s_k-n = p_k / q_n , то коэффициент при x k равен нулю. Поэтому – это многочлен степени не выше k – 1 , . Тогда предыдущее уравнение можно переписать в виде:
(3) .

Это уравнение имеет тот же вид, что и уравнение (1), только значение k стало на 1 меньше. Повторяя эту процедуру k–n раз, получаем уравнение:
,
из которого определяем коэффициенты многочлена U_{n– 1} ( x ) .

Итак, мы определили все неизвестные коэффициенты s_i , u_l . Причем s_k–n ≠ 0 . Лемма доказана.

Деление многочленов

Разделив обе части уравнения (1) на Q_n ( x ) , получим:
(4) .
По аналогии с десятичными числами, S_k–n ( x ) называется целой частью дроби или частным, U_{n– 1} ( x ) – остатком от деления. Дробь многочленов, у которой степень многочлена в числителе меньше степени многочлена в знаменателе называется правильной дробью. Дробь многочленов, у которой степень многочлена в числителе больше или равна степени многочлена в знаменателе называется неправильной дробью.

Уравнение (4) показывает, что любую неправильную дробь многочленов можно упростить, представив ее в виде суммы целой части и правильной дроби.

Деление многочленов уголком

По своей сути, целые десятичные числа являются многочленами, у которых переменная равна числу 10 . Например, возьмем число 265847. Его можно представить в виде:
.
То есть это многочлен пятой степени от 10 . Цифры 2, 6, 5, 8, 4, 7 являются коэффициентами разложения числа по степеням числа 10.

Поэтому к многочленам можно применить правило деления уголком (иногда его называют делением в столбик), применяемое к делению чисел. Единственное отличие заключается в том, что, при делении многочленов, не нужно переводить числа больше девяти в старшие разряды. Рассмотрим процесс деления многочленов уголком на конкретных примерах.

Пример деления многочленов уголком

Выделить целую часть дроби и найти остаток от деления:
.

Здесь в числителе стоит многочлен четвертой степени. В знаменателе – многочлен второй степени. Поскольку 4 ≥ 2 , то дробь неправильная. Выделим целую часть, разделив многочлены уголком (в столбик):

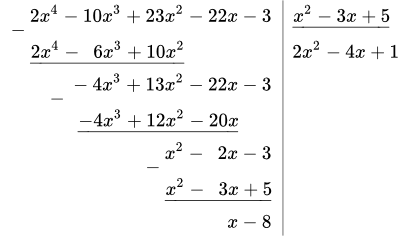
Приведем подробное описание процесса деления. Исходные многочлены записываем в левый и правый столбики. Под многочленом знаменателя, в правом столбике, проводим горизонтальную черту (уголок). Ниже этой черты, под уголком, будет целая часть дроби.

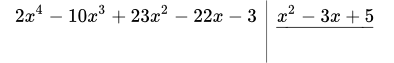
1.1 Находим первый член целой части (под уголком). Для этого разделим старший член числителя на старший член знаменателя: .

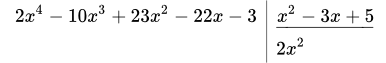
1.2 Умножаем 2 x 2 на x 2 – 3 x + 5 :
. Результат записываем в левый столбик:

1.3 Берем разность многочленов в левом столбике:

.

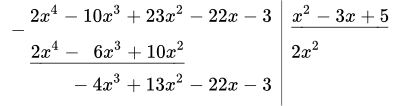
Итак, мы получили промежуточный результат:
.

Дробь в правой части неправильная, поскольку степень многочлена в числителе ( 3 ) больше или равна степени многочлена в знаменателе ( 2 ). Повторяем вычисления. Только теперь числитель дроби находится в последней строке левого столбика.
2.1 Разделим старший член числителя на старший член знаменателя: ;

2.2 Умножаем на знаменатель: ;

2.3 И вычитаем из последней строки левого столбика: ;

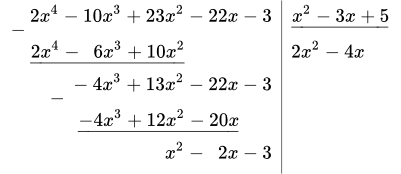
Промежуточный результат:
.

Снова повторяем вычисления, поскольку в правой части стоит неправильная дробь.
3.1 ;
3.2 ;
3.3 ;

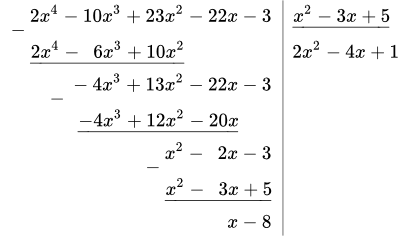
Итак, мы получили:
.
Степень многочлена в числителе правой дроби меньше степени многочлена знаменателя, 1 . Поэтому дробь – правильная.

;
2 x 2 – 4 x + 1 – это целая часть;
x – 8 – остаток от деления.

Пример 2

Выделить целую часть дроби и найти остаток от деления:
.

Выполняем те же действия, что и в предыдущем примере:

Здесь остаток от деления равен нулю:
.

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов:
.

Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

2.3 Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Пример 2

Найти произведение многочленов столбиком:
.

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3 Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

2.3 Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x .

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
.

Автор: Олег Одинцов . Опубликовано: 21-05-2015

Источник