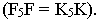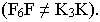- Способ числовых отметок что такое
- Метод с числовыми отметками
- Числовые отметки
- Числовые отметки в строительстве
- Задачи с числовыми отметками
- Задача 1
- Задача 2
- Проекции с числовыми отметками в начертательной геометрии с примерами
- Прямая
- Взаимное положение двух прямых линии
- Параллельные прямые
- Пересекающиеся прямые
- Скрещивающиеся прямые
Способ числовых отметок что такое
Метод с числовыми отметками
В проекциях с числовыми отметками плоскость проекций П i называют плоскостью нулевого уровня и обозначают П 0. Идея этого метода состоит в том, что на плоскость П 0 ортогонально проецируют точку и вместе с проекцией точки задают ее расстояние до плоскости П 0. Это расстояние называют числовой отметкой точки, задают его обычно в метрах. Числовую отметку точки пишут внизу справа от обозначения ее изображения.
Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом. На плане всегда указывают линейный масштаб. При необходимости дают ориентацию относительно сторон света.
Очень удобно в проекциях с числовыми отметками изображать линии уровня, все точки которых имеют одинаковые отметки. Линии уровня проецируются на П 0 без искажения своей формы.
Проекции с числовыми отметками позволяют просто решать многие задачи. Обратимость чертежей в проекциях с числовыми отметками очевидна.
Зарождение идеи этого метода относят к средним векам. Уже тогда многие народы, пользующиеся картами с показаниями морских глубин, умели изображать точку при помощи ее проекции и отметки. Однако теоретическое обоснование метод получил лишь в XIX веке благодаря французскому военному инженеру – капитану Нуазе .
Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине и часто называются однокартинными.
Источник
Числовые отметки
Сущность метода проекций с числовыми отметками заключается в том, что все точки объекта ортогонально проецируются только на одну плоскость проекций (обычно горизонтальную), которую называют плоскостью нулевого уровня (или «нулевой»). Но так как одна проекция не определяет положение точки в пространстве, то фронтальную проекцию заменяют числами (отметками), которые наносят на чертеже около проецируемых точек.
Числовые отметки указывают превышение точек – расстояние от данной точки до плоскости нулевого уровня (обычно в метрах).
При проецировании земной поверхности за абсолютный нулевой уровень принимают постоянный уровень воды в Балтийском море. Иногда прибегают к помощи условного уровня. При этом если точка находится выше плоскости нулевого уровня, ее числовая отметка считается положительной (знак «+» как правило не ставят), а если ниже, то перед значением числовой отметки ставится знак «-».
Чертежи с числовыми отметками называют планами. На планах необходимо вычерчивать линейный масштаб, а иногда масштаб уклонов, которыми пользуются при решении конкретных задач.
Числовые отметки в строительстве
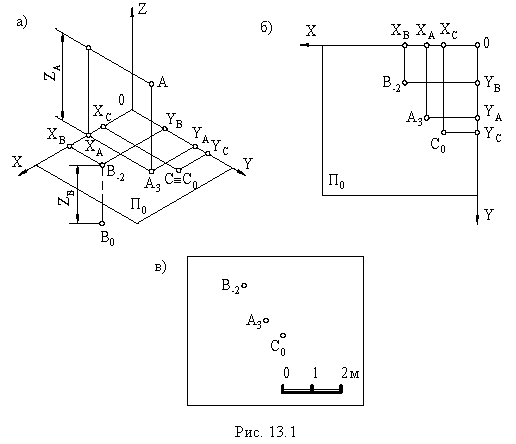
В строительном деле встречаются объекты, размеры которых в плане значительно превышают все остальные. Например, участки земной поверхности с расположенными на них сооружениями, дороги, различные насыпи, аэродромы, строительные площадки и т. п. Для проектирования таких объектов применение обычных ортогональных проекций нецелесообразно. В подобных случаях обычно используют проекции с числовыми отметками, которые отличаются тем, что образуются в результате ортогонального проецирования предмета на горизонтальную плоскость, называемую плоскостью нулевого уровня. Для получения изображения, однозначно соответствующего данному предмету, справа от проекций точек пишут числа, указывающие высоты (обычно в метрах) от данных точек до плоскости нулевого уровня, эти числа называются числовыми отметками (рис. 1).
Поскольку по одной проекции невозможно определить действительное положение точки в пространстве, то для точек в проекциях с числовыми отметками применяют индексы, определяющие расстояние от точки до плоскости проекции, называемой в проекциях с числовыми отметками плоскостью нулевого уровня (π0). Эти индексы, иначе называемые отметками, пишутся справа и внизу от буквы, обозначающей точку, и могут быть положительными или отрицательными в зависимости от того, находится точка выше или ниже плоскости нулевого уровня, например А7, B-5 , С0 (см. рис. 1). Чертежи в проекциях с числовыми отметками обычно снабжаются линейным масштабом.
Прямая в проекциях с числовыми отметками может быть задана двумя точками (рис. 2,а), или одной точкой, но в таком случае должны быть дополнительные сведения о направлении убывания точек и угле наклона прямой к плоскости нулевого уровня (π0). Эта проблема решается указанием стрелки, показывающей убывание отметок и величины угла наклона прямой к плоскости π0 (рис. 2, б). Часто вместо угла наклона удобнее использовать понятие
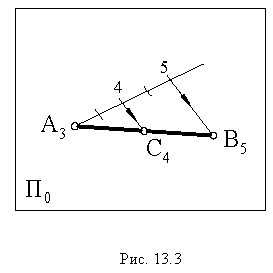
уклона, уклон обозначается буквой i и определяется как тангенс угла наклона прямой к плоскости π0. Как видно из рисунка 3, уклон прямой CB будет равен отношению разности величин B0B4 и C0C4 к величине горизонтальной проекции этой прямой на плоскость π0 (рис. 2, в).
Поскольку горизонтальная проекция отрезка (проекция на плоскость π0) в проекциях с числовыми отметками называется его заложением, а разность отметок начала и конца отрезка называется превышением, то более кратко уклоном отрезка можно назвать отношение его превышения к заложению. Другим важным понятием, характеризующим прямую в проекциях с числовыми отметками, является понятие интервала. Интервалом называется заложение отрезка данной прямой, у которого разность отметок начала и конца равна единице. Интервал обозначается буквой I. Таким образом, уклон и интервал связаны соотношением i =1/I.
Задачи с числовыми отметками
Часто встречающимися задачами, касающимися прямой и точки в проекциях с числовыми отметками, являются следующие:
Задача 1
Градуирование прямой. Под градуированием прямой понимается определение точек прямой с отметками, выраженными целыми числами и отличающимися друг от друга на единицу длины. Прием градуирования прямой показан на рисунке 4
здесь возможны два случая:
а) когда оба конца отрезка имеют одинаковые знаки (рис. 4, а,б). В этом случае от конца отрезка с большой точностью откладывают, перпендикулярно к нему, значения разности отметок и проводят графическое градуирование, как показано на рисунке 4,а. Если концы отрезков имеют дробные отметки, то от конца отрезка с меньшей отметкой откладывают только дробную часть, а от другого откладывают разницу отметок плюс дробную часть отметки конца отрезка. Градуирование при этом выполняют, как показано на рисунке 4, б.
б) случай, когда концы отрезков имеют разные знаки. Построения отличаются лишь тем, что отметки начала и конца отрезка откладываются в противоположные стороны. Пример такого градуирования показан на рисунке 4, в.
Задача 2
Определение взаимного положения пересекающихся отрезков. Во взаимном положении отрезков возможны случаи пересекающихся, скрещивающихся и параллельных отрезков. Для того, чтобы определить, пересекаются или скрещиваются отрезки, достаточно их проградуировать и определить отметки конкурирующих точек, если отметки этих точек 6 одинаковы (точка E на рисунке 5, а), то отрезки пересекаются. В том случае, если отметки конкурирующих точек различны (точки N и P на рисунке 5, б), то отметки скрещиваются.
Выяснение параллельности прямых сводится к проверке следующих условий:
- заложения отрезков параллельны между собой;
- направления возрастания и убывания отметок одинаковы;
интервалы (уклоны) отрезков одинаковы. Так отрезки A4B10 и C8D14, изображенные на рисунке 6, параллельны, если интервал ℓAB, будет равен интервалу ℓCD, так первые два условия параллельности этих прямых уже выполнены.
Источник
Проекции с числовыми отметками в начертательной геометрии с примерами
Содержание:
Метод проекций с числовыми отметками получил широкое применение в инженерно-строительном деле для изображения и проектирования на земной поверхности различных инженерных сооружений (железные и шоссейные дороги, котлованы, каналы, плотины, строительные площадки), а также для изображения земной поверхности. Этот метод применяется в том случае, когда размеры проектируемых объектов по длине значительно превышают размеры по высоте.
Проекции с числовыми отметками представляют собой прямоугольные проекции точек на горизонтальной плоскости, сопровождающиеся числами, указывающими удаление самих точек от этой плоскости.
Горизонтальная плоскость
Положение горизонтальных проекций точек 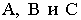
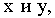
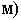
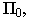
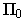
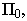
Изображение в проекциях с числовыми отметками, показанное на рис. 13.1, в, обычно называется планом. На планах необходимо вычерчивать линейный масштаб, который используется при решении различных метрических задач.
Прямая
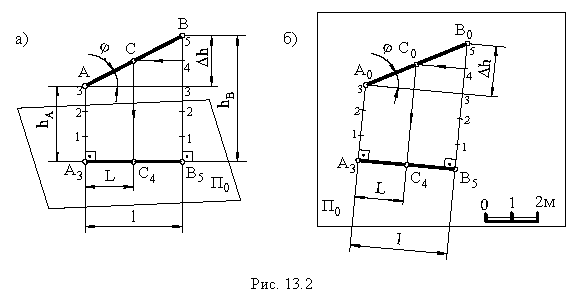
В проекциях с числовыми отметками прямую общего положения можно задавать прямоугольными проекциями двух точек на плоскости нулевого уровня .указав их отметки ( рис.13.2, а и б)
Длина горизонтальной проекции отрезка прямой называется заложением прямой (1).
Точки 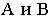
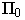
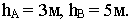
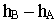
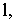
где 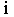
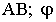
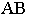
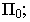
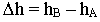
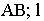
Заложение прямой, соответствующее единице превышения называют интервалом прямой
Если 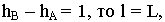
Градуированием прямой называется нахождение на горизонтальной проекции прямой точек с целыми числовыми отметками, разность между которыми равна единице (см. рис. 13.2).
Градуирование прямой можно выполнять разными способами. Один из способов показан на рис. 13.2, б. В этом случае необходимо восстановить перпендикуляры к проекции отрезка в точках 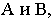
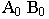
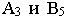
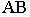
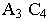
Пропорциональное деление отрезка заключается в делении его горизонтальной проекции на 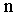
Для нахождения на прямой отметок с целыми числами необходимо провести через точку 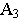
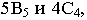
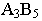
Взаимное положение двух прямых линии
Две прямые в пространстве могут быть взаимно параллельны, могут пересекаться или скрещиваться друг с другом.
Параллельные прямые
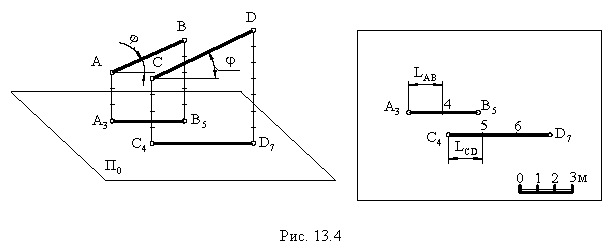
В этом случае их проекции параллельны друг другу, интервалы равны и отметки возрастают в одном направлении (рис. 13.4).
Пересекающиеся прямые
Проекции пересекающихся прямых пересекаются, и в точке пересечения проекций прямые имеют одинаковую отметку.
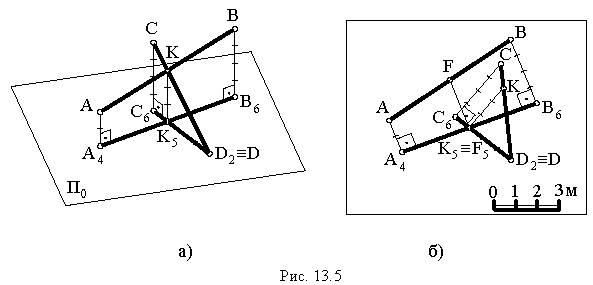
На рис. 13.5, а изображены прямые, горизонтальные проекции которых пересекаются Чтобы определить, пересекаются ли эти прямые в пространстве, необходимо найти отметки точек пересечения прямых в пересечении их проекций.
На рис 13.5, б для определения взаимного положения прямых 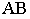
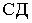
- градуируем прямые
Для этого восстанавливаем перпендикуляры из точек
к соответствующим проекциям прямых и откладываем на перпендикулярах отрезки, равные высотам точек;
- получив натуральные величины прямых
определяем отметки точек пересечения прямых в пересечении их проекций
- прямые
пересекаются, так как отметки точек
и
равны
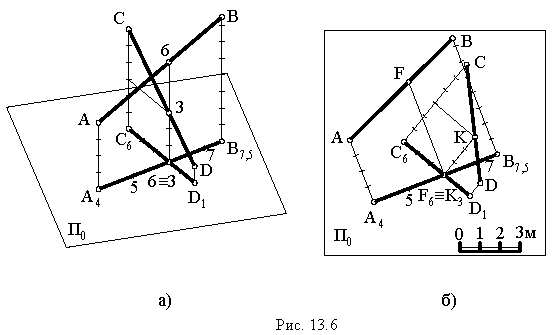
Скрещивающиеся прямые
Проекции скрещивающихся прямых пересекаются, и в точке пересечения их проекций прямые имеют разные числовые отметки. На рис. 13.6, а показаны проекции скрещивающихся прямых, которые пересекаются. Числовые отметки в точке пересечения проекций определяем так же, как в предыдущей задаче. На рис. 13.6, б видно, что в точке пересечения проекций прямые имеют неодинаковые отметки
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Перспектива
- Построение окружности
- Цилиндрическая винтовая линия
- Определение и задание поверхностей на чертеже
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Решение задач на тему: перпендикулярности прямой и плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник






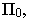
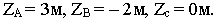
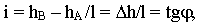
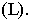
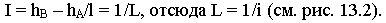
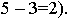
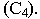
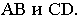 Для этого восстанавливаем перпендикуляры из точек
Для этого восстанавливаем перпендикуляры из точек 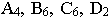 к соответствующим проекциям прямых и откладываем на перпендикулярах отрезки, равные высотам точек;
к соответствующим проекциям прямых и откладываем на перпендикулярах отрезки, равные высотам точек;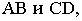 определяем отметки точек пересечения прямых в пересечении их проекций
определяем отметки точек пересечения прямых в пересечении их проекций 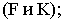
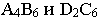 пересекаются, так как отметки точек
пересекаются, так как отметки точек 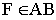 и
и 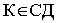 равны
равны