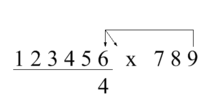Способ быстрого счета трахтенберга объяснение

Способ быстрого счета трахтенберга объяснение

Система Трахтенберга — система устного счёта, разработанная математиком Яковом Трахтенбергом во время заключения в нацистском концлагере. Состоит из нескольких частей — методов умножения на числа от 2 до 12, метода умножения произвольных натуральных чисел и другого.

Общее умножение

Пусть даны два числа — и , выглядящие в десятичной записи как и . Стандартный алгоритм умножения на предписывает умножить на все разряды по очереди и сложить результаты, учитывая их сдвиг. Трахтенберг предлагает взамен считать -ый разряд ответа как сумму переноса из предыдущего разряда и , не записывая промежуточные вычисления.

по дистрибутивности: слагаемые с влияют на разряд только в виде переноса, а с n>»/> — вообще не влияют.

Например, умножим 12345 на 21.

перенос		Всего	Цифра
0	5*1	5	5
0	4*1+5*2	14	4
1	3*1+4*2	12	2
1	2*1+3*2	9	9
0	1*1+2*2	5	5
0	1*2	2	2

Итого, читая снизу вверх, получается 259245. Яков Трахтенберг предлагает делать вычисления, записанные в таблице выше, в уме, выписывая только результат.

Частные правила умножения

Умножение на 11

Правило: Добавь цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 3425 × 11 = 37675

3425 × 11 = (0+3)(3+4)(4+2)(2+5)(5+0) = 37675

Умножение на 12

Правило: Добавь удвоенную цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 2413 × 12 = 28956

2413 × 12 = (0×2+2)(2×2+4)(4×2+1)(1×2+3)(3×2+0) = 28956

Умножение на 13

Правило: Добавь утроенную цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 5876 × 13 = 76388

5876 × 13 = (0×3+5)(5×3+8)(8×3+7)(7×3+6)(6×3+0) = 76388

Умножение на 14

Правило: Добавь учетверённую цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 4859 × 14 = 68026

4859 × 14 = (0×4+4)(4×4+8)(8×4+5)(5×4+9)(9×4+0) = 68026

Умножение на 17

Правило: Добавь цифру, умноженную на разряд единиц, к её соседу справа, не забывая про перенос через разряд.

Пример: 5739 × 17 = 97563

5739 × 17 = (0×7+5)(5×7+7)(7×7+3)(3×7+9)(9×7+0) = 97563

Источник

Система Трахтенберга — Trachtenberg system

Система Трахтенберга — это система быстрого мысленного расчета . Система состоит из ряда легко запоминаемых операций, которые позволяют очень быстро выполнять арифметические вычисления. Он был разработан русским инженером Яковом Трахтенбергом для того, чтобы занять его разум во время пребывания в нацистском концентрационном лагере .

В оставшейся части статьи представлены некоторые методы, разработанные Трахтенбергом. Некоторые из разработанных Трахтенбергом алгоритмов предназначены для общего умножения, деления и сложения. Кроме того, система Трахтенберга включает некоторые специализированные методы умножения малых чисел от 5 до 13 (но здесь показано 2-12).

Раздел о сложении демонстрирует эффективный метод проверки вычислений, который также может быть применен к умножению.

СОДЕРЖАНИЕ

Общее умножение, математическая теория Трахтенберга

Метод общего умножения — это метод достижения умножения с небольшой пространственной сложностью, то есть как можно меньше временных результатов, которые можно хранить в памяти. Это достигается за счет того, что последняя цифра полностью определяется умножением последней цифры множимого . Это временный результат. Чтобы найти предпоследнюю цифру, нам нужно все, что влияет на эту цифру: временный результат, последняя цифра, умноженная на предпоследнюю цифру , а также предпоследняя цифра, умноженная на последнюю цифру . Этот расчет выполнен, и у нас есть временный результат с правильными двумя последними цифрами. а × б <\ displaystyle a \ times b> а <\ displaystyle a> б <\ displaystyle b> а <\ displaystyle a> б <\ displaystyle b>

В общем, для каждой позиции в итоговом результате мы суммируем все : п <\ displaystyle n> я <\ displaystyle i>

а (цифра в я ) × б (цифра в ( п — я ) ) . <\ displaystyle a <\ text <(цифра at>> i <\ text <)>> \ times b <\ text <(цифра at>> (ni) <\ text <)>>.>

Люди могут изучить этот алгоритм и, таким образом, умножить в уме четырехзначные числа, записывая только конечный результат. Они писали его, начиная с крайней правой цифры и заканчивая крайней левой цифрой.

Трахтенберг определил этот алгоритм с помощью своего рода попарного умножения, при котором две цифры умножаются на одну цифру, по существу, сохраняя только среднюю цифру результата. При выполнении описанного выше алгоритма с этим попарным умножением требуется еще меньше временных результатов.

Пример: 123456 × 789 <\ displaystyle 123456 \ times 789>

Чтобы найти первую (крайнюю правую) цифру ответа, начните с первой цифры множимого:

Цифра единиц 9 × 6 я s 4. <\ displaystyle 9 \ times 6 \ равно \ 4.> Первая цифра ответа . Десятая цифра игнорируется. 4 <\ displaystyle 4> 5 <\ displaystyle 5>

Чтобы найти вторую цифру ответа, начните со второй цифры множимого:

Цифра единиц плюс цифра десятков плюс 9 × 5 <\ displaystyle 9 \ times 5> 9 × 6 <\ displaystyle 9 \ times 6> Цифра единиц измерения . 8 × 6 <\ displaystyle 8 \ times 6> 5 + 5 + 8 знак равно 18 <\ displaystyle 5 + 5 + 8 = 18> . Вторая цифра ответа заключается в том, и нести к третьей цифре. 8 <\ displaystyle 8> 1 <\ displaystyle 1>

Чтобы найти третью цифру ответа, начните с третьей цифры множимого:

Цифра единиц плюс цифра десятков плюс 9 × 4 <\ displaystyle 9 \ times 4> 9 × 5 <\ displaystyle 9 \ times 5> Цифра единиц плюс цифра десятков плюс 8 × 5 <\ displaystyle 8 \ times 5> 8 × 6 <\ displaystyle 8 \ times 6> Цифра единиц 7 × 6 <\ displaystyle 7 \ times 6> 1 + 6 + 4 + 4 + 0 + 2 знак равно 17 <\ displaystyle 1 + 6 + 4 + 4 + 0 + 2 = 17> Третья цифра ответа — и переносится на следующую цифру. 7 <\ displaystyle 7> 1 <\ displaystyle 1>

Чтобы найти четвертую цифру ответа, начните с четвертой цифры множимого:

Цифра единиц плюс цифра десятков плюс 9 × 3 <\ displaystyle 9 \ times 3> 9 × 4 <\ displaystyle 9 \ times 4> Цифра единиц плюс цифра десятков плюс 8 × 4 <\ displaystyle 8 \ times 4> 8 × 5 <\ displaystyle 8 \ times 5> Цифра единиц плюс цифра десятков . 7 × 5 <\ displaystyle 7 \ times 5> 7 × 6 <\ displaystyle 7 \ times 6> 1 + 7 + 3 + 2 + 4 + 5 + 4 знак равно 26 <\ Displaystyle 1 + 7 + 3 + 2 + 4 + 5 + 4 = 26> переносится с третьей цифры. Четвертая цифра ответа — и переносится на следующую цифру. 6 <\ displaystyle 6> 2 <\ displaystyle 2>

Продолжите тем же способом, чтобы получить оставшиеся цифры.

Трахтенберг назвал это методом двух пальцев. Расчеты для нахождения четвертой цифры из приведенного выше примера показаны справа. Стрелка от девятки всегда будет указывать на цифру множимого непосредственно над цифрой ответа, который вы хотите найти, а другие стрелки указывают на одну цифру вправо. Каждая стрелка указывает на пару UT или пару продуктов. Вертикальная стрелка указывает на продукт, где мы получим цифру единиц, а наклонная стрелка указывает на продукт, где мы получим десятки цифр пары продуктов. Если стрелка указывает на пробел без цифры, для этой стрелки нет расчетов. По мере того, как вы решаете каждую цифру, вы перемещаете каждую стрелку над множителем на одну цифру влево, пока все стрелки не укажут на нули с префиксом.

Деление в системе Трахтенберга выполняется так же, как и в умножении, но с вычитанием вместо сложения. Разделение дивиденда на более мелкие частичные дивиденды с последующим делением этого частичного дивиденда только на крайнюю левую цифру делителя даст ответ по одной цифре за раз. Когда вы решаете каждую цифру ответа, вы затем вычитаете пары продуктов (пары UT), а также пары NT (числа-десятки) из частичного дивиденда, чтобы найти следующий частичный дивиденд. Пары продуктов находятся между цифрами ответа и делителем. Если вычитание дает отрицательное число, вам нужно скопировать одну цифру и уменьшить эту цифру ответа на единицу. При достаточной практике этот метод можно выполнять в уме.

Общее дополнение

Метод добавления столбцов чисел и точной проверки результата без повторения первой операции. Производится промежуточная сумма в виде двух рядов цифр. Ответ получается путем суммирования промежуточных результатов с помощью L-образного алгоритма. В качестве последнего шага пропагандируемый метод проверки одновременно устраняет риск повторения любых исходных ошибок и идентифицирует точный столбец, в котором ошибка возникает. Он основан на контрольных (или цифровых) суммах, таких как метод девяти остатков.

Чтобы процедура была эффективной, различные операции, используемые на каждом этапе, должны отличаться друг от друга, в противном случае существует риск вмешательства.

Другие алгоритмы умножения

При выполнении любого из этих алгоритмов умножения следует применять следующие «шаги».

Ответ должен быть найден по одной цифре, начиная с наименее значащей цифры и двигаясь влево. Последнее вычисление ведется по начальному нулю множимого.

У каждой цифры есть сосед , т. Е. Цифра справа. Соседом самой правой цифры является конечный ноль.

Операция «половинки» имеет особое значение для системы Трахтенберга. Предполагается, что это означает «половину цифры, округленную в меньшую сторону», но из соображений скорости людям, которые следуют системе Трахтенберга, рекомендуется сделать этот процесс уменьшения вдвое мгновенным. Поэтому вместо того, чтобы думать «половина из семи — это три с половиной, поэтому три», предлагается подумать «семь, три». Это значительно ускоряет расчет. Таким же образом запоминаются таблицы для вычитания цифр из 10 или 9.

И всякий раз, когда правило требует добавления половины соседа, всегда добавляйте 5, если текущая цифра нечетная. Это компенсирует потерю 0,5 при вычислении следующей цифры.

Умножение на 2

Правило : умножьте каждую цифру на 2 (с переносом).

Пример: 8624 x 2

Работаем слева направо:

8 + 8 = 16, 6 + 6 = 12 (неся 1), 2 + 2 = 4 4 + 4 = 8;
8624 х 2 = 17248

Пример: 76892 x 2

Работаем слева направо:

7 + 7 = 14 6 + 6 = 12 8 + 8 = 16 9 + 9 = 18 2 + 2 = 4;
76892 х 2 = 153784

Умножение на 3

1. Вычтите крайнюю правую цифру из 10.
2. Вычтите оставшиеся цифры из 9.
3. Удвойте результат.
4. Добавьте половину соседа справа плюс 5, если цифра нечетная.
5. Для начального нуля вычтите 2 из половины соседнего.

Пример: 492 × 3 = 1476.

Работаем справа налево:

(10-2) × 2 + половина от 0 (0) = 16. Напишите 6, перенесите 1. (9 — 9) × 2 + Половина из 2 (1) + 5 (так как 9 нечетно) + 1 (переносится) = 7. Запишите 7. (9-4) × 2 + половина из 9 (4) = 14. Запишите 4, перенесите 1. Половина из 4 (2) — 2 + 1 (перенос) = 1. Запишите 1.

Умножение на 4

1. Вычтите самую правую цифру из 10.
   1. Вычтите оставшиеся цифры из 9.
2. Добавьте половину соседа плюс 5, если цифра нечетная.
3. Для ведущего 0 вычтите 1 из половины соседнего.

Пример: 346 × 4 = 1384.

Работаем справа налево:

(10-6) + половина от 0 (0) = 4. Напишите 4. (9-4) + половина из 6 (3) = 8. Напишите 8. (9 — 3) + половина из 4 (2) + 5 (так как 3 нечетно) = 13. Запишите 3, перенесите 1. Половина из 3 (1) — 1 + 1 (перенос) = 1. Запишите 1.

Умножение на 5

• Правило : возьмите половину соседа, затем, если текущая цифра нечетная, добавьте 5.

Пример: 42 × 5 = 210

Половина соседа 2, конечный ноль, равна 0. Половина соседа 4 — 1. Половина соседа ведущего нуля равна 2. 43 × 5 = 215 Половина соседа 3 равна 0, плюс 5, потому что 3 нечетно, равно 5. Половина соседа 4 — 1. Половина соседа ведущего нуля равна 2. 93 × 5 = 465 Половина соседа 3 равна 0, плюс 5, потому что 3 нечетно, равно 5. Половина соседа 9 равна 1, плюс 5, потому что 9 нечетное, равно 6. Половина соседа ведущего нуля равна 4.

Умножение на 6

1. К каждой цифре прибавьте половину соседа. Если текущая цифра нечетная, добавьте 5.

Пример: 357 × 6 = 2142.

Работаем справа налево:

У 7 нет соседа, добавьте 5 (так как 7 нечетно) = 12. Запишите 2, перенесите 1. 5 + половина 7 (3) + 5 (так как начальная цифра 5 нечетная) + 1 (переносится) = 14. Напишите 4, перенесите 1. 3 + половина из 5 (2) + 5 (так как 3 нечетно) + 1 (переносится) = 11. Запишите 1, перенесите 1. 0 + половина из 3 (1) + 1 (переносится) = 2. Запишите 2.

Умножение на 7

1. Удвойте каждую цифру.
2. Добавьте половину своего соседа (отбрасывая десятичные дроби, если они есть).
3. Если основная цифра нечетная, добавьте 5.

Пример: 523 × 7 = 3661

Работаем справа налево:

3 × 2 + 0 + 5 = 11, 1. 2 × 2 + 1 + 1 = 6. 5 × 2 + 1 + 5 = 16, 6. 0 × 2 + 2 + 1 = 3.

Умножение на 8

1. Вычтите самую правую цифру из 10.
   1. Вычтите оставшиеся цифры из 9.
2. Удвойте результат.
3. Добавьте соседа.
4. Для начального нуля вычтите 2 из соседнего.

Пример: 456 × 8 = 3648.

Работаем справа налево:

(10-6) × 2 + 0 = 8. Напишите 8. (9-5) × 2 + 6 = 14, запишите 4, перенесите 1. (9 — 4) × 2 + 5 + 1 (переносится) = 16. Напишите 6, перенесите 1. 4 — 2 + 1 (переносится) = 3. Запишите 3.

Умножение на 9

1. Вычтите самую правую цифру из 10.
   1. Вычтите оставшиеся цифры из 9.
2. Добавьте соседа к сумме
3. Для начального нуля вычтите 1 из соседнего.

Для правил 9, 8, 4 и 3 только первая цифра вычитается из 10. После этого каждая цифра вычитается из девяти.

Пример: 2130 × 9 = 19 170

Работаем справа налево:

(10-0) + 0 = 10. Напишите 0, перенесите 1. (9 — 3) + 0 + 1 (переносится) = 7. Запишите 7. (9 — 1) + 3 = 11. Запишите 1, перенесите 1. (9 — 2) + 1 + 1 (переносится) = 9. Запишите 9. 2 — 1 = 1. Запишите 1.

Умножение на 11

1. Добавьте цифру к ее соседу. (Под «соседом» мы подразумеваем цифру справа.)

Пример: 3 , 425 × 11 знак равно 37 , 675 <\ displaystyle 3,425 \ times 11 = 37,675>

(0 + 3) (3 + 4) (4 + 2) (2 + 5) (5 + 0) 3 7 6 7 5

3425 × 11 знак равно 3425 × ( 10 + 1 ) <\ Displaystyle 3425 \ раз 11 = 3425 \ раз (10 + 1)> → 37675 знак равно 34250 + 3425 <\ displaystyle \ rightarrow 37675 = 34250 + 3425>

Умножение на 12

Правило: умножить на 12 :
Начиная с самой правой цифры, удваивайте каждую цифру и складывайте соседнюю. («Сосед» — это цифра справа.)

Если ответ больше одной цифры, просто перенесите лишнюю цифру (которая будет 1 или 2) в следующую операцию. Оставшаяся цифра — это одна цифра окончательного результата.

Пример: 316 × 12 <\ displaystyle 316 \ times 12>

Определите соседей по множимому 0316:

• цифра 6 не имеет правого соседа
• цифра 1 имеет сосед 6
• у цифры 3 есть сосед 1
• цифра 0 (с префиксом ноль) имеет соседа 3

6 × 2 знак равно 12 (2 переносят 1) 1 × 2 + 6 + 1 знак равно 9 3 × 2 + 1 знак равно 7 0 × 2 + 3 знак равно 3 0 × 2 + 0 знак равно 0 316 × 12 знак равно 3 , 792 <\ displaystyle <\ begin 6 \ times 2 & = 12 <\ text <(2 carry 1)>> \\ 1 \ times 2 + 6 + 1 & = 9 \\ 3 \ times 2 + 1 & = 7 \\ 0 \ times 2 + 3 & = 3 \\ 0 \ times 2 + 0 & = 0 \\ [10pt] 316 \ times 12 & = 3,792 \ end >>

Публикации

• Рушан Зиатдинов, Саджид Муса. Система быстрых мысленных вычислений как инструмент развития алгоритмического мышления младших школьников . European Researcher 25 (7): 1105-1110, 2012 [1] .
• Скоростная система базовой математики Трахтенберга, разработанная Яковом Трахтенбергом, А. Катлером (переводчиком), Р. МакШейном (переводчиком), была опубликована Doubleday and Company, Inc., Гарден-Сити, Нью-Йорк, в 1960 году.

Книга содержит конкретные алгебраические объяснения каждой из вышеперечисленных операций.

Большая часть информации в этой статье взята из оригинальной книги.

Алгоритмы / операции умножения и т. Д. Могут быть выражены другими, более компактными способами, которые книга не определяет, несмотря на главу, посвященную алгебраическому описанию.

В популярной культуре

Американский фильм 2017 года « Одаренные» вращается вокруг вундеркинда, который в возрасте 7 лет впечатляет своего учителя, производя вычисления в ее голове с использованием системы Трахтенберга.

Другие системы

В ментальной математике есть много других методов вычислений. В приведенном ниже списке показаны несколько других методов расчета, хотя они могут быть не совсем умственными.

• Книга Бхарати Кришны Тиртхи «Ведическая математика »
• Мысленные счеты. По мере того, как ученики привыкают управлять счетами пальцами, их обычно просят произвести вычисления, визуализируя счеты в своей голове. Почти все опытные пользователи счётов умеют делать арифметические операции в уме.
• Чисанбоп

Программное обеспечение

Ниже приведены известные программы и источники, доступные в качестве учебных пособий.

• Ведическая математическая академия [2]
• Математика скорости Трахтенберга [3]

• Математика Меркурия [4]
• Умножение без таблицы умножения (на iPhone и iPad) [5]

• Таблица умножения без времен — Google Play [6] , Amazon [7] , Barnes and Noble [8]

Источник