Способ борьбы с выбросами данных

Обнаружение и удаление выбросов в Python – легко понять гид

Здравствуйте, читатели! В нашей серии обработки и анализа данных сегодня мы посмотрим на обнаружение и удаление выбросов в Python.

Автор: Pankaj Kumar
Дата записи

Здравствуйте, читатели! В нашей серии обработки данных и анализа данных сегодня мы посмотрим на Обнаружение и удаление выбросов в питоне.

Итак, давайте начнем!

Что такое выбросы в Python?

Перед погружением глубоко в концепцию Выбросы Давайте понять происхождение необработанных данных.

Необработанные данные, которые подаются в систему, обычно генерируются от опросов и извлечения данных из действий в реальном времени в Интернете. Это может привести к изменению данных в данных, и существует вероятность ошибки измерения при записи данных.

Это когда выбросы вступают в сцену.

Оформление – это точка или набор точек данных, которые лежат от остальных значений данных набора данных Отказ То есть это точка данных, которые отображаются вдали от общего распределения значений данных в наборе данных.

Выбросы возможны только в непрерывных значениях. Таким образом, обнаружение и удаление выбросов применимы только к значениям регрессии.

В основном, выбросы, по-видимому, расходятся от общего правильного и хорошо структурированного распределения элементов данных. Это можно считать как Ненормальное распределение, которое появляется вдали от класса или население.

Поняв концепцию выбросов, давайте сейчас сосредоточимся на необходимости удаления выбросов в предстоящем разделе.

Почему необходимо удалить выбросы от данных?

Как обсуждалось выше, выбросы являются точками данных, которые лежат вдали от обычного распределения данных и приводит к тому, что ниже воздействие на общее распределение данных:

• Влияет на общую стандартную вариацию данных.
• Манипулирует общее среднее значение данных.
• Преобразует данные в перекошенную форму.
• Это вызывает смещение в оценке точности модели обучения машины.
• Влияет на распределение и статистику набора данных.

Из-за вышеуказанных причин необходимо обнаружить и избавиться от выбросов до моделирования набора данных.

Обнаружение выбросов – IQR подход

Выбросы в наборе данных могут быть обнаружены методами ниже:

• Z-счет
• Рассеянные участки
• Межструйный диапазон (IQR)

В этой статье мы реализуем метод IQR для обнаружения и лечения выбросов.

IQR – аббревиатура для межступного диапазона Отказ Он измеряет статистическую дисперсию значений данных как мера общего распространения.

IQR эквивалентен разницей между первым квартилем (Q1) и третьим квартилью (Q3) соответственно.

Здесь Q1 относится к первому квартилю I.e. 25% и Q3 относится к третьему квартилю I.e. 75%.

Мы будем использовать Boxplots для обнаружения и визуализации выбросов, присутствующих в наборе данных.

Коробки изображают распределение данных с точки зрения квартилей и состоит из следующих компонентов

• Q1-25%
• Q2-50%
• Q3-75%
• Нижняя граница/усы
• Верхний усы/граница

Любая точка данных, которая лежит ниже нижней границы, и над верхней границей рассматривается как выброс.

Давайте теперь будем реализовать BoxPlot для обнаружения выбросов в приведенном ниже примере.

Пример :

Первоначально мы импортировали набор данных в окружающую среду. Вы можете найти набор данных здесь Отказ

Кроме того, мы сегрегировали переменные в числовые и категорические значения.

Мы применяем BoxPlot, используя BoxPlot () Функция на числовых переменных, как показано ниже:

Как видно выше, вариабельная «ветряная скорость» содержит выбросы, которые лежат над нижней границей.

Удаление выбросов

Сейчас самое время лечить выбросы, которые мы обнаружили, используя BoxPlot в предыдущем разделе.

Используя IQR, мы можем следовать приведенному ниже подходу для замены выбросов в нулевое значение:

• Рассчитайте первый и третий квартиль (Q1 и Q3).
• Кроме того, оцените межквартирный диапазон, IQR-Q1 Отказ
• Оцените нижнюю границу, ниже * 1.5
• Оцените верхнюю границу, Верхний * 1.5.
• Замените точки данных, которые лежат за пределами нижней и верхней границы с Нулевое значение Отказ

Таким образом, мы использовали numpy.percentile () Метод Для расчета значений Q1 и Q3. Кроме того, мы заменили выбросы с numpy.nan как нулевые значения.

Заменив выбросы NAN, давайте теперь проверьте сумму нулевых значений или отсутствующих значений, используя код ниже:

Сумма подсчета нулевых значений/выбросов в каждом столбце набора данных:

Теперь мы можем использовать любую из приведенных ниже методов для лечения нулевых значений:

• Вмешивает недостающие значения со средним, средним или навязчивым значениями.
• Снимите нулевые значения (если пропорция сравнительно меньше)

Здесь мы бросили бы нулевые значения, используя Pandas.dataframe.dropna () функция

Обработавшись к выбросам, давайте теперь проверяем наличие отсутствующих или нулевых значений в наборе данных:

Таким образом, все выбросы, присутствующие в наборе данных, были обнаружены и обработаны (удалены).

Заключение

По этому, мы подошли к концу этой темы. Не стесняйтесь комментировать ниже, если вы столкнетесь с любым вопросом.

Для более таких постов, связанных с Python. Оставайтесь настроиться и до тех пор, до тех пор, пока, счастливое обучение !! 🙂.

Источник

Выброс

Выброс (англ. outlier) — это экстремальные значения во входных данных, которые находятся далеко за пределами других наблюдений. Например, все предметы на кухне имеют температуру около 22-25 грудусов Цельсия, а — духовка 220.

Многие алгоритмы машинного обучения чувствительны к разбросу и распределению значений признаков обрабатываемых объектов. Соответственно, выбросы во входных данных могут исказить и ввести в заблуждение процесс обучения алгоритмов машинного обучения, что приводит к увеличению времени обучения, снижению точности моделей и, в конечном итоге, к снижению результатов. Даже до подготовки предсказательных моделей на основе обучающих данных выбросы могут приводить к ошибочным представлениям и в дальнейшем к ошибочной интерпретации собранных данных.

Содержание

Виды выбросов [ править ]

На основе размерности изучаемого массива данных выбросы подразделяют на одномерные и многомерные.

Одномерные выбросы Точка является выбросом только по одной из своих координат. Многомерные выбросы Точка является выбросом сразу по нескольким координатам.

Другой подход классификации выбросов — по их окружению.

Точечные выбросы Единичные точки, выбивающиеся из общей картины. Точечные аномалии часто используются в системах контроля транзакций для выявления мошенничества, например, когда с украденной карты совершается крупная покупка. Контекстуальные выбросы Для того, чтобы определить, является ли точка выбросом необходим контекст. Например, в Петербурге +15 градусов Цельсия. Зимой такая температура является выбросом, а летом нет. Коллективные выбросы Здесь выбросом является не точка, а группа точек. Примером таких выбросов могут служить, например, задержки поставок на фабрике. Одна задержка не является выбросом. Но если их много, значит это может стать проблемой.

Причины возникновения выбросов [ править ]

• Сбой работы оборудования;
• Человеческий фактор;
• Случайность;
• Уникальные явления;
• и др.

Примеры [ править ]

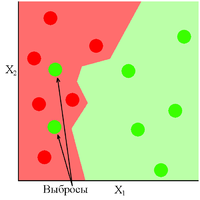
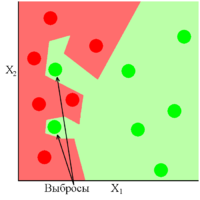
Рис 2 показывает хорошо обученную модель, в которой присутствуют два выброса. Как видно из рисунка данная модель показала себя устойчивой к выбросам, либо же вовремя прекратила своё обучение. Обратная ситуация обстоит с Рис 3, где модель сильно переобучилась из-за присутствующих в ней выбросов.

Методы обнаружения и борьбы с выбросами [ править ]

Методы обнаружения выбросов [ править ]

1. Экстремальный анализ данных(англ. extreme value analysis). При таком анализе не применяются какие-либо специальные статистические методы. Обычно этот метод применим для одномерного случая. Алгоритм использования таков:
   • Визуализировать данные, используя диаграммы и гистограммы для нахождения экстремальных значений;
   • Задействовать распределение, например Гауссовское, и найти значения, чье стандартное отклонение отличается в 2-3 раза от математического ожидания или в полтора раза от первой либо третьей квартилей;
   • Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели;
2. Аппроксимирующий метод (англ. proximity method). Чуть более сложный метод, заключающийся в применении кластеризующих методов;
   • Использовать метод кластеризации для определения кластеров в данных;
   • Идентифицировать и отметить центроиды каждого кластера;
   • Соотнести кластеры с экземплярами данных, находящимися на фиксированном расстоянии или на процентном удалении от центроида соответствующего кластера;
   • Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели;
3. Проецирующие методы (англ. projections methods). Эти методы довольно быстро и просто определяют выбросы в выборке;
   • Использовать один из проецирующих методов, например, метод главных компонент (англ. principal component analysis, PCA[1] ) или самоорганизующиеся карты Кохонена(англ. self-organizing map, SOM[2] ) или проекцию Саммона(англ. Sammon mapping, Sammon projection[3] ), для суммирования обучающих данных в двух измерениях;
   • Визуализировать отображение;
   • Использовать критерий близости от проецируемых значений или от вектора таблицы кодирования (англ. codebook vector) для идентифицирования выбросов;
   • Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели.

Локально взвешенное сглаживание [ править ]

Локально взвешенное сглаживание (англ. LOcally WEighted Scatter plot Smoothing, LOWESS) [4] . Данная методика была предложена Кливлендом (Cleveland) в 1979 году для моделирования и сглаживания двумерных данных [math]X^m=<(x_i, y_i)>_^m[/math] . Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. Локально-линейная модель может быть записана в виде: [math]y_t=\alpha_t+\beta_t x_t + \varepsilon_t[/math] . Эта модель может быть расширена на случай локально-квадратичной зависимости и на модель с большим числом независимых переменных. Параметры [math]\alpha_t[/math] и [math]\beta_t[/math] локально линейной модели оцениваются с помощью локально взвешенной регрессии, которая присваивает объекту тем больший вес, чем более близок он к объекту t. Степень сглаживания определяется параметром сглаживания [math]f[/math] , который выбирает пользователь. Параметр [math]f[/math] указывает какая доля (англ. fraction) данных используется в процедуре. Если [math]f = 0.5[/math] , то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если [math]f = 0.8[/math] , то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше, чем они ближе к объекту [math]t[/math] .

Постановка задачи [ править ]

Пусть задано пространство объектов $X$ и множество возможных ответов [math]Y = \mathbb[/math] . Существует неизвестная зависимость [math]y^*\colon X \to Y[/math] , значения которой известны только на объектах обучающией выборки [math]X^l = (x_i\ ,\ y_i)^l_,\ y_i = y^*(x_i)[/math] . Требуется построить алгоритм [math]a\colon X\to Y[/math] , аппроксимирующий неизвестную зависимость [math]y^*[/math] . Предполагается, что на множестве $X$ задана метрика [math]\rho(x,x’)[/math] .

Также стоит определить следующее. Для вычисления [math]a(x) = \alpha[/math] для [math]\forall x \in X[/math] воспользуемся методом наименьших квадратов: [math]Q(\alpha;X^l) = \sum_^l \omega_i(x)(\alpha-y_i)^2 \rightarrow \underset<\alpha \in \mathbb>[/math] , где [math]\omega_i[/math] — это вес $i$-ого объекта.

Веса [math]\omega_i[/math] разумно задать так, чтобы они убывали по мере увеличения расстояния [math]\rho(x,x_i)[/math] . Для этого можно ввести невозрастающую, гладкую, ограниченную функцию [math]K:[0, \infty) \rightarrow [0, \infty)[/math] , называемую ядром [на 28.01.19 не создан] , и представить [math]\omega_i[/math] в следующем виде:

[math]\omega_i(x) = K\left(\frac<\rho(x,x_i)> \right )[/math] , где $h$ — ширина окна.

Приравняв равной нулю производную [math]\frac<\partial Q> <\partial \alpha>= 0[/math] и выразив [math]\alpha[/math] , получаем формулу Надарая-Ватсона [5] : [math]a_h(x;X^l) = \frac<\sum_^ y_i\omega_i(x)><\sum_^ \omega_i(x)> = \frac<\sum_^ y_iK\left(\frac<\rho(x,x_i)> \right )><\sum_^ K\left(\frac<\rho(x,x_i)> \right )>[/math] .

Проблема выбросов в этой задаче [ править ]

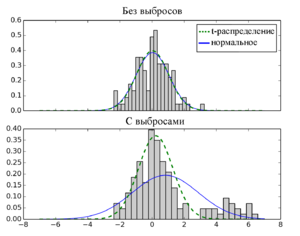
Большие случайные ошибки в значениях [math]y_i[/math] сильно искажают оценку Надарая-Ватсона.

Идея [ править ]

Чем больше величина невязки [math]\varepsilon_i = \left | a_h\left (x_i;X^\ell\backslash\left \ \right )-y_i\right |[/math] , тем меньше должен быть вес i-го объекта [math]\omega_i(x)[/math] .

Эвристика [ править ]

Домножить веса [math]\omega_i(x)[/math] на коэффициенты [math]\gamma_i = \widetilde\left ( \varepsilon_i \right )[/math] , где [math]\widetilde\left ( \varepsilon \right )[/math] — ещё одно ядро, вообще говоря, отличное от [math]K\left ( \rho \right )[/math] .

Псевдокод [ править ]

Пример на языке R [ править ]

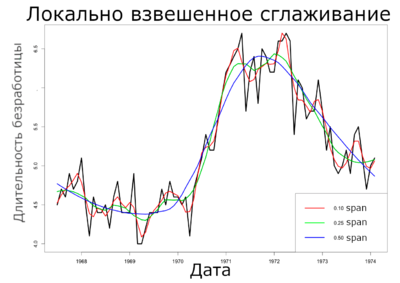
В этом примере мы попытаемся локально регрессировать и сгладить среднюю продолжительность безработицы на основе набора экономических данных из пакета $ggplot2$ языка $R$. Мы рассматриваем только первые 80 строк для этого анализа, чтобы легче было наблюдать степень сглаживания на приведенных ниже графиках.

Другие алгоритмы борьбы с выбросами [ править ]

В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются робастными. Метод локально взвешенного сглаживания относится к робастным методам, так как он устойчив к наличию небольшого количества выбросов.

• Дерево принятия решения (англ. decision tree[6] ). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится к робастным методам;
• Робастная регрессия (англ. robust regression[7] ). В отличие от регрессии, использующей, например, метод наименьших квадратов, в этом алгоритме не строится идеализированное предположение, что вектор ошибок [math]\varepsilon[/math] распределен согласно нормальному закону. Однако на практике зачастую имеют место отклонения от этого предположения. Тогда можно применить метод наименьших модулей (англ. Least Absolute Deviation, LAD[8] ) в случае, если распределение ошибок измерений подчиняется распределению Лапласа (англ. Laplace distribution [9] ).

Источник