Способ бога кубик рубик

Как сложить кубик Рубика новичку по алгоритму бога? Дополненная реальность приходит на помощь

Несмотря на то, что кубику Рубика уже много десятков лет, эта головоломка продолжает оставаться популярной. Ставятся рекорды — как людьми, так и роботами, совершенствуется алгоритм решения головоломки. Причем сейчас компьютеры уже могут научить собирать Кубик человека с любым уровнем опыта (речь здесь идет о приложениях обучающих, коих немало). Правильно собрать все грани после пары дней обучения при помощи компьютера смогут даже те, кто взял игрушку в руки в первый раз.

К слову, чемпион мира по сборке кубика Рубика (да, есть и такие чемпионы) решает головоломку всего за 4,9 секунды. Чемпиона зовут Лукас Эттер, это подросток из США. Аналогичный рекорд для роботизированной системы составляет уже 0,887 секунды (правда, этот результат еще не подтвержден). Но как научиться быстро собирать кубик Рубика самостоятельно? Можно тренироваться (на это могут уйти многие годы). А можно воспользоваться специальной программой, которая поможет собрать кубик в минимальное число ходов (так называемый алгоритм бога). Здесь никакие тренировки не нужны, приложение делает все само.

Вот так собирает кубик чемпион-человек:

А так — чемпион-компьютер:

Вообще говоря, существует множество алгоритмов для сборки головоломки. Для обычного человека среднее число ходов составляет около 40. Немногие чемпионы умеют собирать кубик по алгоритму бога. Если кратко, то так называют алгоритм, который требует для сборки любой начальной конфигурации минимальное количество ходов. Для кубика Рубика это число равно 20.

А теперь вернемся к дополненной реальности. Разработчик по имени Martin Španěl создал приложение Mistr Kostky, которое помогает собирать кубик Рубика человеку. Причем число ходов как раз то самое — ровно 20. Приложение может определять состояние 2-3 граней кубика одновременно, а для распознавания получаемых изображений используется библиотека OpenCV.

В дополненной реальности показывается, как нужно вращать грани головоломки, чтобы достичь оптимального количества ходов. Разработчик создал свою программу в рамках научной работы — он является студентом Карлова университета (Прага).

Работает программа в два этапа. На первом происходит распознавание состояния каждой грани. После того, как система завершает первый этап, начинается второй — приложение показывает пользователю, куда и как нужно вращать грани кубика для решения головоломки (иногда получается это сделать менее, чем за 20 ходов).

Интересно, что если владелец головоломки ошибается, то приложение приходится перезапускать — оно не в состоянии перестроиться «на лету». Отмечу, что приложения для решения кубика рубика появились не сейчас. Это одно из лучших, да, но еще в 2009 году в каталог приложений Apple была добавлена программа Cube Cheater. Она помогала пользователю найти решение по фотографии граней.

Изначально автор создавал свое приложение под Android, но обещал выпустить и версию под другие платформы. Вот ветка обсуждения Mistr Kostky на Reddit.

Источник

Алгоритм Бога Кубика Рубика 3х3

Маленькая пластмассовая игрушка-головоломка созданная венгерским скульптором Эрне Рубиком, стала самой популярной головоломкой в мире. В 1974 году профессор архитектуры для наглядного объяснения теории групп своим студентам создал всеми известную головоломку, названую в последствии Кубиком Рубика.

Ее суть состоит в том, что 26 маленьких кубиков, образуют куб большего размера с гранями по 3 кубика (3х3х3) установленными на центральном шарнире. Каждая грань кубика, состоящая из 9 малых кубиков, имеет свой цвет.

Спустя год, когда Эрне Рубик понял, что его изобретение становится популярным среди его учеников, он запатентовал головоломку. А уже через 7 лет был проведен первый мировой чемпионат по сборке Кубика Рубика. В 1982г. победителем первых соревнований стал студент из Лос-Анджелеса Minh Thai (Мин Тай) с результатом в 22,95 секунды.

Эти соревнования дали толчок любителям головоломки для составления своих алгоритмов сборки Кубика Рубика за наименьшее число вращений. Минимальное количество ходов, определяющее полную сборку головоломки, назвали – Алгоритм Бога кубика Рубика.

История создания формулы Бога

Английским математиком было выдвинуто утверждение, что собрать Кубик Рубика из любого положения можно за 23 хода. И, именно это число, на протяжении долгих лет

считалось числом бога. Но спустя 35 лет компания Google доказала, что для того, чтобы собрать кубик Рубика из любого положения за наименьшее число ходов, достаточно всего 20 поворотов граней кубика. С тех пор Алгоритм бога кубика Рубика 3х3 составляет всего 20 ходов. В ходе поиска наименьшего числа ходов сборки кубика были найдены множества алгоритмов, вычисляющих наименьшее число различных элементов кубика Рубика, верхней или фронтальной поверхности кубика.

В современном мире существуют сотни и даже тысячи различных комбинаций, позволяющих быстро собрать кубик Рубика 3 на 3, как правило все они составляют 40 и более поворотов кубика.

35 лет прошло со дня создания кубика Рубика до того момента, как ученым удалось создать универсальную формулу для сборки Кубика Рубика 3х3, названную – «Алгоритмом Бога».

Формула Бога кубика Рубика 3 на 3

Стоит отметить, что несмотря на созданную универсальную формулу сборки кубика Рубика 3 на 3, она все же не позволяет на 100% собирать головоломку.

Формула бога выглядит так:

B2 D2 F I R2 F U2 R2 F I R2 U2 F R U L B D R I D L2 U I

Лишь усредняет все имеющиеся комбинации для сборки кубика и решает головоломку только в 95% случаях. Поэтому если у вас не получилось собрать кубик с первого раза по формуле бога, попробуйте еще раз, возможно, вы попали именно в те 5% вариантов, которые не учитывает формула.

Расшифровка формулы Бога (Этапы сборки)

Для того, чтобы вам было удобнее понимать как необходимо вращать кубик, рассмотрим отдельно каждое значение формулы.

B2 (back) — поворот задней стороны кубика по часовой стрелке 2 раза

D2 (down) — поворот нижней стороны кубика по часовой стрелке 2 раза

F I (front) — поворот фронтальной (передней) части кубика против часовой стрелки 1 раз

R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза

F (front) — поворот фронтальной (передней) части кубика по часовой стрелке 1 раз

U2 (up) — поворот верхней стороны кубика по часовой стрелке 2 раза

R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза

F I (front) — поворот фронтальной (передней) части кубика против часовой стрелки 1 раз

R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза

U2 (up) — поворот верхней стороны кубика по часовой стрелке 2 раза

F (front) — поворот фронтальной (передней) части кубика по часовой стрелке 1 раз

R (right) — поворот правой стороны кубика по часовой стрелке 1 раз

U (up) — поворот верхней стороны кубика по часовой стрелке 1 раз

L (left) — поворот левой стороны кубика по часовой стрелке 1 раз

Формула бога русскими буквами:

Т2 Н2 Ф I П2 Ф В2 П2 Ф I П2 В2 Ф П В Л Т Н П I Н Л2 В I

ВНИМАНИЕ. Многие начинающие любители головоломки Рубика невнимательно производят вращение по формуле бога и тем самым не могут собрать кубик. Говоря о том, что формула не работает. Мы лишь предлагаем вам попробовать собрать кубик вновь, но более внимательно отнестись к вращениям граней, особенно когда их нужно вращать против часовой стрелки.

Ну и, конечно же, нужно помнить, что формула бога описывает лишь 95% комбинаций и не всегда может подходить для сборки кубика Рубика 3х3.

Источник

Кубик Рубика за 20 шагов

Любая позиция Кубика Рубика может быть решена не более, чем за 20 шагов.

Несколько лет назад было доказано, что для Кубика Рубика есть решение за 23 хода. Теперь это число сократилось до 20. Чтобы это сделать, потребовалось 35 (тридцать пять) лет компьютерного времени, пожертвованного Гуглом.

Каждый блок решения использовал свой алгоритм — последовательность шагов для достижения нужной конфигурации. Например, один алгоритм предназначался для решения верхней грани, а другой — для позиционирования средних краев. Есть множество различных алгоритмов, различающихся по степени сложности и количеству требуемых шагов, но те, которые может запомнить человек, обычно требуют больше 40 шагов.

Разумно полагать, что Бог может использовать более эффективный алгоритм, который решает задачу за наикратчайшее число шагов. Этот алгоритм известен как “алгоритм Бога”. Число шагов в худшем случае называется числом Бога. В конце концов, было показано, что это число — 20.

После изобретения Кубика Рубика пятнадцать лет ушло на поиск позиции, которая наверняка решается за 20 шагов. Через 15 лет после этого мы докажем, что 20 шагов достаточно для любой позиции.

История числа Бога

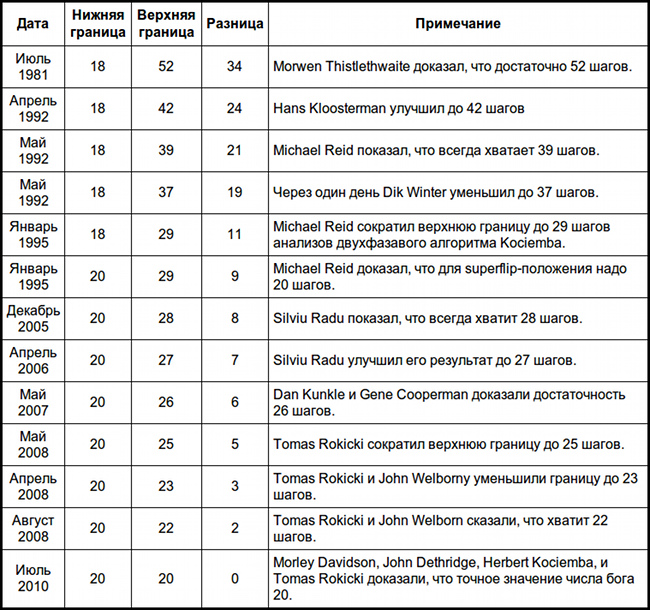
К 1980 году было установлено, нижняя граница — 18, а верхняя — вероятно, около 80. В таблице ниже собраны все результаты:

Как мы это сделали

Как мы справились с 43 252 003 274 489 856 000 позициями Кубика Рубика?

• Мы разделили все позиции на 2 217 093 120 множеств — по 19 508 428 800 позиций в каждом.
• Мы уменьшили число множеств для решения до 55 888 296 на основе симметрии и покрытии множества.
• Мы не искали оптимальное решение, а только решения с длиной 20 или менее шагов.
• Мы написали программу, находящее решение для одного множества за 20 секунд.
• Потребовалось 35 лет компьютерного времени для поиска решений всех конфигураций в каждом из 55 888 296 множеств.

Деление пространства позиций

Мы разбили большую задачу на 2 217 093 120 меньших подзадач: в каждую входило по 19,508,428,800 различных позиций. Одна такая подзадача легко помещается в память современного компьютера, и этот метод позволил достаточно быстро получить решение.

Симметрия

Если повертеть Кубик Рубика влево-вправо или вверх-вниз, то, по сути, ничего не изменится: число шагов в решении останется тем же самым. Вместо того, чтобы решать все эти позиции, можно получить решение для одной и распространить его на повернутые позиции. Есть 24 различных ориентации в пространстве и 2 зеркальных положения Кубика для каждой позиции, что позволяет уменьшить число решаемых позиций в 48 раз. Если использовать аналогичные рассуждения и воспользоваться поиском задачи “покрытия множества”, то число подзадач уменьшается от 2 217 093 120 до 55 882 296.

Хорошие и оптимальные решения

Оптимальное решение содержит достаточное количество шагов, но не больше, чем надо. Так как уже известна одна позиция, для которой требуется 20 шагов, то мы можем не искать оптимальное решение для каждой позиции, а только решения в 20 или менее шагов. Это многократно убыстряет задачу.

Оборудование

У нас была возможность решить 55 882 296 подзадач на мощностях Гугла и выполнить все вычисления за несколько недель. Гугл не раскрывает характеристики компьютеров, но было затрачено 1.1 миллиард секунд компьютерного времени (Intel Nehalem, four-core, 2.8GHz) на выполнение расчетов.

Самая трудная позииция

Мы знали в течении 15 лет, что есть позиции, которые требует 20 шагов, но мы доказали, что ни для одной позиции и не надо больше.

Позиции с решениями в 20 шагов редки, но их вполне возможно встретить в реальности. Вероятность встретить такую позицию варьируется от 10^(-9) до 10^(-8). Мы точно не знаем точное количество таких позиций. Таблица дает оценку числа позиций для каждой длины решения.

Для длин от 16 и больше, числа являются примерными. Наши исследования подтвердили все первоначальные данные до 14 строки включительно, а 15 строка — новый результат. На 11 августа мы обнаружили 12 миллионов позиций с длиной решения 20. Эта позиция была самой сложной для наших программ:

Источник

Удивительная математика внутри кубика Рубика

В прошлом году исполнилось 40 лет с того времени, как человечество узнало о кубике Рубика. Эта головоломка сразу смутила умы почти полумиллиарда энтузиастов, которые полагали, что могут раскрыть сумасшедшие секреты этого удивительного кубика, если разберут его на составные части.

В преддверии юбилея кубика Рубика (да, юбилея!) и стартов новых потоков курсов Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science, пришло время раз и навсегда разгадать эту головоломку, на этот раз с помощью довольно сложной математики. Физические внутренности кубика могут быть изготовлены из пластика, но его виртуальными внутренностями, конечно же, являются числа. Давайте же окунёмся в этот мир чисел.

Разбор кубика Рубика на блоки

Начнем с базовых знаний. Кубик Рубика размером 3x3x3 имеет шесть граней, каждая своего цвета. Центральный кубик каждой грани прикреплён к внутренней крестовине, скрепляющей все элементы куба. Центральные кубики могут только вращаться вокруг своей оси. Одни и те же цвета всегда располагаются напротив друг друга; на стандартном кубе белый цвет находится напротив жёлтого, красный – напротив оранжевого, синий – напротив зелёного.

Если разобрать кубик Рубика, можно увидеть, что он состоит из трёх типов составных блоков. Первый тип: центральная крестовина, на которой удерживаются центральные кубики каждой грани. Второй тип – маленькие кубики размером 1x1x1. Угловые кубики имеют три цветные стороны, бортовые кубики – две. Кубик Рубика имеет одну крестовину, восемь угловых кубиков и двенадцать бортовых кубиков.

С помощью математики мы можем узнать общее количество способов, которыми можно перемешать кубик Рубика: 43 252 003 274 489 856 000. В виде математической формулы это число можно представить следующим образом: (3 8 8!)(2 12 12!)/12. Вот как получается эта формула.

Первый элемент, 3 8 , определяет количество возможных вариантов вращения восьми угловых кубиков. Угловой кубик можно вставить в паз, который может поворачиваться тремя разными способами. То есть для каждого из восьми угловых кубиков множитель равняется 3, поэтому происходит умножение до 3 8 .

Далее учитываем перемещения каждого углового кубика. Всего угловых пазов восемь, поэтому у первого углового кубика есть восемь вариантов. У второго углового кубика остается семь вариантов, у следующего слева кубика – шесть вариантов и так далее, вплоть до последнего углового кубика, который должен войти в последний угловой паз. Это даёт факториал 8!.

Таким образом, первая часть формулы (3 8 8!) осуществляет подсчёт всех способов, которыми угловые кубики могут размещаться в кубе. Значение 3 8 – это их ориентация, а 8! – их положение.

В следующей части формулы (2 12 12!) применяется тот же принцип, но теперь для ребер. Рёбра имеют только две ориентации, поэтому 12 рёбер могут иметь в общей сложности 2 12 ориентаций. Всего имеется 12 положений, поэтому 12! представляет собой количество способов, которыми кубики могут быть размещены в таких положениях.

Что ещё осталось в формуле (3 8 8!)(2 12 12!)/12? Осталось деление на 12. Деление на 12 связано с одной особенностью кубика Рубика, о которой многим известно, но которую не до конца её понимают. Проведём мысленный эксперимент (который, возможно, вы уже проводили вживую!):

Предположим, вы разобрали кубик Рубика, вытащили из него все кубики, а затем вставили все кубики обратно в случайные пазы (при этом угловые кубики можно установить только в углы, а бортовые кубики – только на рёбра). Вы получите конструкцию, которая выглядит как обычный перемешанный кубик, и на данный момент мы подсчитали все возможные комбинации созданного таким образом куба: (3 8 8!)(2 12 12!). Теперь зададим вопрос, всегда ли можно собрать такой перемешанный кубик, не разбирая его на части?

Здесь кроется ловушка, в которую попадало множество начинающих любителей разгадывать эту головоломку. Если вы тренируетесь и хотите перемешать уже собранный куб, необходимо сохранить куб в целости и собрать его вручную. Если разобрать куб на части и собрать кубики случайным образом, вероятность того, что головоломку можно будет решить, составит всего 1 к 12.

Ответ кроется в алгоритмах

Хотите понять, почему вероятность составит всего 1 к 12? Есть хороший визуальный способ понять, почему вероятность именно такая. Шанс собрать разобранный на составные кубики и снова случайным образом перемешанный большой куб будет равен шансам собрать куб со следующими образцами граней:

Оранжевая, жёлтая и зелёная стороны грани (не показаны) собираются как обычно.

Мы разместили их таким образом, чтобы было понятно, как получается коэффициент 12. Ряд 1 имеет нормальные углы. У рядов 2 и 3 один угол повёрнут. Столбец 1 имеет нормальные рёбра. У столбцов 2 и 3 одно ребро повёрнуто. У столбца 3 два ребра поменяны местами. И, наконец, в столбце 4 одно ребро повёрнуто и два ребра поменяны местами.

Таким образом, 12 кубов, представленных выше на фотографиях, не могут быть преобразованы друг в друга. 13-го варианта, который нельзя преобразовать ни в один из таких 12 кубов, не существует. Откуда нам это может быть известно?

Между тем, что может и что не может быть сделано посредством перемещения граней куба, есть связь. Последовательность перемещений граней куба энтузиасты сборки часто называют «алгоритмом». Популярными алгоритмами являются те, которые перемещают лишь несколько кубиков, оставляя остальные нетронутыми. Число 12 возникло по той причине, что на такие алгоритмы накладываются ограничения.

Число 12 составляется из трёх множителей: 12 = 3 * 2 * 2. Откуда берутся множитель 3 и два множителя 2?

Множитель 3: существует алгоритм, который поворачивает каждый из двух разных углов, но нет алгоритма, который поворачивает один угол (оставляя все остальные нетронутыми). Другими словами, если взять обычный кубик Рубика, вынуть один из его углов и заменить его на повёрнутый, такой куб собрать будет невозможно, то есть вы переместитесь из верхнего левого угла нашей диаграммы в одну из клеток прямо под ним.

Однако, если повторить эту операцию и повёрнуть еще один угол, второй множитель 3 не добавится. Теперь, когда в кубе повёрнуто два угла, мы можем последовательно применять алгоритм, поворачивающий два угла, до тех пор, пока не зафиксируется по крайней мере один из углов. Если другой угол случайно встанет на своё место, можем считать, что нам повезло и такой куб можно собрать. Ориентация углов может быть троякой.

Рассуждения относительно первого множителя 2 аналогичны. Существует алгоритм, поворачивающий на свое место каждое из двух разных рёбер, но алгоритма, способного повернуть на своё место только одно ребро, не существует. Таким образом, любое количество повёрнутых ребер может быть сведено к одному ребру, которое в итоге либо окажется, либо не окажется повёрнутым – варианта всего два.

Последний множитель 2 фактически относится к граням и углам, хотя на диаграмме мы показали его с гранями. Существует алгоритм, меняющий местами два угла, одновременно меняя местами два ребра. Но нет ни одного алгоритма, который был бы способен менять местами ни только пару углов, ни только пару рёбер.

Возьмите куб, вытащите два ребра и поменяйте их местами – на диаграмме вы попадёте на столбец, расположенный либо между столбцами 1 и 3, либо между столбцами 2 и 4. Аналогичные рассуждения можно применить, если поменять местами пару углов. Однако перемена местами пары ребер и пары углов уравновешивает баланс, так как алгоритм выхода из таких состояний существует.

Итак, после того как мы объяснили, откуда взялись все множители в коэффициенте 12, можно понять, откуда взялась формула (3 8 8!)(2 12 12!)/12. Число всех возможных положений кубиков в кубе составляет (3 8 8!)(2 12 12!), но только двенадцатая часть таких положений годится для сборки куба. Таким образом, число (3 8 8!)(2 12 12!)/12 обозначает количество способов, которыми можно перемешать кубик Рубика, не разбирая его на части.

Доказательство Популярной механики

Если вы достаточно любопытны, то, наверное, захотите проверить, верны ли сделанные выше утверждения. Существуют ли более сложные математические приемы, которые могут доказать, что «алгоритма, способного повернуть на своё место только один бортовой кубик, не поворачивая любой другой кубик, не существует»? Да, такие математические приёмы существуют. Вот как примерно строится такое математическое доказательство:

При переворачивании грани куба происходит перемещение четырёх бортовых кубиков. Рассмотрим, к примеру, алгоритм из 10 перемещений. Для каждого кубика выполните алгоритм и посчитайте, сколько раз перемещался кубик, и назовите это количество «числом перемещений кубика». Сложите эти числа для каждого бортового кубика, всего должно получиться 40 перемещений кубиков, так как каждое из 10 перемещений добавляет к сумме четверку.

В общем случае для любого алгоритма общее число перемещений бортовых кубиков должно быть кратно 4. Теперь пара важных фактов: если бортовой кубик перемещать чётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь такую же ориентацию. И наоборот, если бортовой кубик перемещать нечётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь перевёрнутую ориентацию.

Естественно, сказанное выше можно доказать с использованием более сложных математических методов, но мы не собираемся сильно углубляться в математику, иначе объём данной статьи превзойдёт все мыслимые и немыслимые пределы. Эти два факта также можно проверить экспериментально, чтобы понять, что всё происходит именно так. (В этом доказательстве поворот на 180 градусов считается двумя перемещениями каждого соответствующего кубика.)

Теперь давайте рассмотрим гипотетический алгоритм, достигающий цели, поворачивающий один бортовой кубик, оставляя при этом в неприкосновенности другой кубик. Одно повёрнутое ребро было перемещено алгоритмом нечётное количество раз, а каждое из 11 остальных рёбер было перемещено чётное количество раз. Сумма 11 чётных чисел и одного нечётного числа всегда нечётна, но мы показали ранее, что такая сумма должна быть кратна 4. Может ли нечётное число быть кратно 4? Нет, не может. Следовательно, такого алгоритма не существует.

Теперь вы понимаете, что число (3 8 8!)(2 12 12!)/12 представляет собой количество возможных состояний куба. Но для изучающего куб математика это лишь предварительная информация. Перед тем как начинать применять более сложные математические методы, задайте себе главный вопрос: «Существуют ли в этой теме математические вопросы, оставшиеся без ответов?»

Число Бога и многое другое

Главной задачей, поставленной изобретателем головоломки, естественно, была сборка куба. Эрно Рубик (Ernő Rubik) создал первый прототип головоломки в 1974 году, и через шесть лет она поступила в массовую продажу. Естественно, он был первым, которому удалось собрать куб.

В 1980 году кубик Рубика стал хитом продаж в магазинах игрушек. Но некоторые математики уже несколько лет экспериментировали с его ранними версиями. Одним из них был доктор Дэвид Сингмастер (David Singmaster) – составитель знаменитого путеводителя «Записки о Волшебном кубике Рубика» и разработавший нотацию для записи операций поворота граней куба. Эта нотация стала стандартом и теперь известна как нотация Сингмастера.

Если бы это была статья писалась в 1980-х годах, то, возможно, стоило бы подробнее объяснить читателям, что такое нотация Сингмастера, и использовать её при описании алгоритмов сборки куба. Множество авторов статей так и делали. Но сегодня на Youtube выложено множество видеоинструкций, поэтому в этой статье мы не будем отвлекаться на описание нотации.

За последние несколько десятилетий рекорд сборки кубика Рубика на время постоянно обновлялся. На сегодня мировой рекорд сборки кубика Рубика человеком составляет 3,47 секунды. В 1997 году доктор Джессика Фридрих разработала самый известный, самый скоростной и самый гибкий метод быстрой сборки кубика Рубика Самые быстрые сборщики кубика Рубика сегодня пользуются разными вариантами сборки от доктора Фридрих.

По мере того как одни пользователи оттачивали мастерство сборки, другие пытались решать важные математические вопросы, связанные с этой головоломкой. За сколько ходов можно собрать куб независимо от того, в каком состоянии он первоначально находился? Если кто-то перемешал куб за 500 ходов, то, естественно, собрать его можно менее чем за 500 ходов. На насколько именно меньше ходов?

Соответственно, была поставлена главная математическая задача: существует ли магическое число, позволяющее сказать: «любой перемешанный куб может быть собран именно за такое количество ходов [или меньше]»? Благодаря остроумному замечанию, что для обретения чувства уверенности нужно божественное вмешательство, это число получило название «Число Бога».

Первая гипотеза о существовании Числа Бога была выдвинута доктором Морвеном Тистлетвэйтом (Morwen Thistlethwaite) в 1981 году, который доказал, что это число существует и не превышает 52. Другими словами, любой перемешанный куб может быть собран за 52 хода или меньше.

В 1990–2000-х годах математики пошли ещё дальше. В июне 2010 года группа из четырёх учёных доказала, что Число Бога равняется 20. На этом веб-сайте, который ведут эти учёные, представлены самые последние знания о кубике Рубика.

Другими словами, какое бы хаотичное первоначальное состояние ни имел Кубик Рубика, его всегда можно собрать за 20 или менее ходов.

Для математиков в теме кубика Рубика остались лишь небольшие лакомые кусочки. Число Бога определено и равняется 20. Но точно неизвестно, сколько именно из 43 252 003 274 489 856 000 комбинаций потребуют для сборки полных 20 ходов.

Количество комбинаций, для сборки которых требуется ровно один ход, составляет 18. Это значение легко рассчитать. Есть шесть граней и три способа поворота каждой из них. Сколько кубов можно собрать ровно за два или три хода? Для математиков эта задача сложности не представляет, но можно предположить, что с увеличением количества ходов также будет увеличиваться сложность вычислений. Сегодня математики уже добрались до числа ходов 15; мы точно знаем количество комбинаций, для сборки которых требуется ровно 15 ходов, но пока не вполне точно представляем количество комбинаций для числа ходов от 16 до 20.

И это – последняя нерешённая задача в математической теме кубика Рубика. Будем ждать, когда кто-либо её решит. Может быть, это будете вы?

Получите нужные знания и навыки на курсе Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science. А промокод HABR даст скидку 50%.

Узнайте, как прокачаться в других специальностях или освоить их с нуля:

Источник