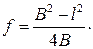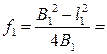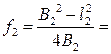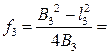Собирающей линзы методом Бесселя
Указанный выше метод определения главных фокусов является приближенным. Бессель предложил точный способ нахождения главных фокусных расстояний линз. Он заключается в том, что предмет и экран остаются неподвижными, а перемещается только линза, которую нужно устанавливать в двух положениях: в первом положении линза дает увеличенное изображение, а во втором положении линза дает уменьшенное изображение. Из формулы для нахождения фокусного расстояния собирающей линзы: 
видно, что величины аи вможно менять местами. Такая замена означает, что если на место изображения А1В1 в положении (б) (Рис.16.3) поставить предмет АВ из положения (а), то изображение в случае (б) предмета АВ получится в том же месте, где раньше был предмет. Исходя из рис.16.3.а и б, следует, что:
. Решая совместно эту систему уравнений относительно аив , получим:
. (16.4)
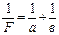
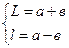
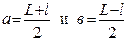
Подставляя (16.4) в (16.3), получим формулу нахождения главного фокусного расстояния собирающей линзы методом Бесселя: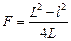 
. (16.5)
Порядок выполнения задания №2
1. На оптическую скамью поставить собирающую линзу и предмет.
2. Расположить экран и предмет на таком расстоянии друг от друга, чтобы, перемещая между ними линзу, можно было получить два отчетливых изображения (увеличенное и уменьшенное) предмета.
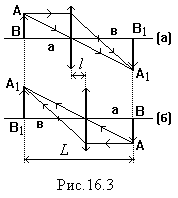
3. Измерить расстояние L (рис.16.3) между экраном и предметом.
4. Перемещая линзу, получить увеличенное изображение предмета на экране, заметить по линейке положение линзы. Затем, передвигая линзу, получить уменьшенное изображение предмета, заметить по линейке положение линзы. Вычислить расстояние l между двумя положениями линзы.
5. Меняя положение предмета и линзы, повторить измерения ещё два раза.
6. По формуле (16.5) вычислить фокусное расстояние. Рассчитать его среднее значение. Оценить погрешности измерений.
7. По среднему значению фокусного расстояния, по формуле (16.1) рассчитать оптическую силу линзы.
8. Результаты измерений и вычислений занести в таблицу 2.
| № | L, м | l, м | F, м | , м | DF, м | e, % | F= ± , м | , дптр |
Вычисления к заданию №2:
Контрольные вопросы защиты лабораторной работы:
1. Что называется линзой? Какие существуют типы линз?
2. Дайте определение фокуса линзы. Чем отличаются фокусные расстояния и оптические силы собирающей и рассеивающей линз?
3. Какие существуют виды аберраций? Как их устранить?
4. Нарисуйте и объясните принцип построения изображения в собирающей линзе.
5. Объясните принцип определения фокусного расстояния собирающей линзы двумя методами.
6. Запишите и объясните формулы: линзы, её фокусного расстояния и оптической силы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Метод Бесселя (метод перемещения линзы)
Если расстояние между предметом и экраном более четырех фокусных расстояний, то с помощью собирающей линзы можно получить два резких изображения предмета – увеличенное и уменьшенное при двух положениях линзы I и II (рис. 6). При этом оба положения линзы будут симметричны относительно середины отрезка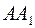 
.
Расстояние от предмета до линзы определяется как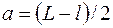 
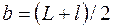
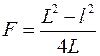, а расстояние от линзы до экрана – 
. Подставляя эти величины в формулу тонкой линзы, получим:
 . | (3) |
Этот способ теоретически является наиболее точным. Во всех других способах, измеряя расстояние до линзы, подразумевают ее середину, на самом деле эти расстояния следует отсчитывать от соответствующих главных плоскостей, определение которых довольно затруднительно.
 |
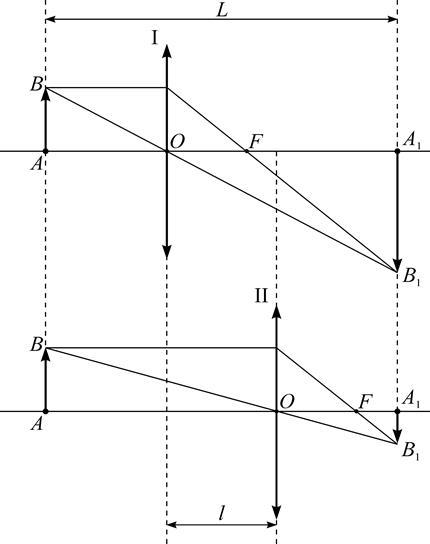| Рис. 6. Метод Бесселя |
В описанном способе ошибка исключается благодаря тому, что в нем измеряется не расстояние от линзы, а ее перемещение.
Фокусное расстояние рассеивающей линзы
Если на пути лучей, выходящих из точки B и сходящихся в точке Э перед преломлением в собирающей линзе (рис. 7) поставить рассеивающую линзу так, чтобы расстояние от нее до точки B было меньше фокусного, то действительный фокус лучей удаляется от собирающей линзы. Лучи, исходящие из точки В теперь сместятся в точку A.
 |
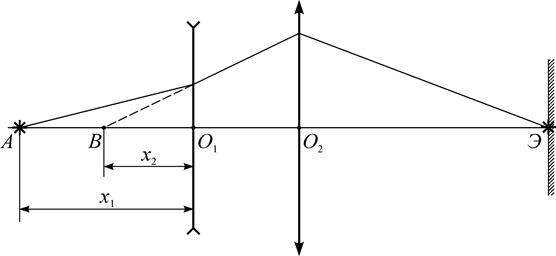| Рис. 7. Определения фокусного расстояния рассеивающей линзы |
Вследствие этого можно считать точку А действительным источником, а точку В ее мнимым изображением.
Обозначив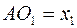 
, 
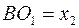
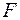
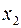
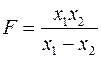и учитывая знаки ( 
и 
– отрицательны) по формуле тонкой линзы получим:
 . | (4) |
2.3. Приборы и принадлежности:
Источник
Определение фокусных расстояний положительной и отрицательной линз с помощью метода Бесселя
Санкт-Петербургский Государственный Университет
Информационных Технологий, Механики и Оптики
Лабораторная работа № 3
ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ПОЛОЖИТЕЛЬНОЙ И ОТРИЦАТЕЛЬНОЙ ЛИНЗ С ПОМОЩЬЮ МЕТОДА БЕССЕЛЯ
Санкт-Петербург
Цель работы – определение фокусных расстояний положительной и отрицательной линз с помощью метода Бесселя.
Фокусное расстояние тонкой положительной ( собирающей ) линзы можно легко рассчитать, если с помощью этой линзы на экране получить действительное изображение предмета: 
,
где 
— главное фокусное расстояние тонкой линзы; 
— расстояние от линзы до изображения; S – расстояние от линзы до предмета.
Однако у реальных (не тонких) линз все отрезки отсчитываются не от сферических поверхностей линзы, а от главных плоскостей, которые в общем случае не совпадают с поверхностями линзы. Главные плоскости могут лежать и внутри и вне линзы, совершенно несимметрично относительно ее сферических поверхностей. Главная плоскость представляет собой геометрическое место точек пересечения лучей, падающих на линзу параллельно главной оптической оси, и лучей, выходящих из линзы после преломления на двух ее поверхностях.
На рис. 1 H и 
— главные плоскости линзы; 
— заднее фокусное расстояние линзы.
Для расчета фокусного расстояния по формуле линзы в отрезках необходимо знать расстояния S и 
, отсчитанные от главных плоскостей линзы, положение которых, как правило, неизвестно.
Точные методом определения величины 
линзы является метод Бесселя, который принципиально исключает влияние на результат местоположения главных плоскостей линзы.
Метод Бесселя заключается в следующем: если на оптической скамье расстояние между предметом y и экраном, на котором получается изображение предмета 
, взято больше четырех фокусных расстояний положительной линзы, то существуют два симметричных положения линзы, при которых на экране получаются четкие изображения предмета (рис. 2). При первом положении линзы на экране получается увеличенное изображение предмета 
, при втором – уменьшенное 
. ( L – расстояние от предмета до экрана; А – расстояние между двумя положениями линзы).
Выражая отрезки S1, 
, S2, 
через L и А, пренебрегая отрезком d по сравнению с L и подставляя их в формулу линзы, получаем:
. (1)
Как видно из этой формулы, для вычисления фокусного расстояния положительной линзы достаточно знать расстояние от предмета до экрана L и расстояние между двумя положениями линзы А, которым соответствуют увеличенное и уменьшенное изображения предмета. Значения обоих этих отрезков (А и L) никак не связаны с положением главных плоскостей линзы, что и является главным достоинством метода Бесселя.
Непосредственно с помощью метода Бесселя определить фокусное расстояние отрицательной линзы невозможно, так как такая линза не дает действительных изображений на экране. Однако если отрицательную линзу вплотную сложить с такой положительной линзой, что они дадут положительную оптическую систему, фокусное расстояние такой системы можно будет определить по методу Бесселя. Оптическая сила системы линз, сложенных вплотную, определяется как сумма оптических сил отдельных линз системы, поэтому
. (2)
Определив по методу Бесселя f /пол и f /сист, можно рассчитывать и фокусное расстояние отрицательной линзы f /отр.
Поместить в оправу одну положительную линзу и, перемещая ее по оптической скамье, найти два положения, при которых на экране образуются увеличенное и уменьшенное изображения предмета. Отметить положения линзы по шкале и расстояние от предмета до экрана. Опыт повторить при другом значении L, отличающемся от первого не менее, чем на 30 см. При каждом значении L величину смещения линзы А определить не менее трех раз. Вычислить фокусное расстояние положительной линзы по формуле (1) дважды при двух значениях L по средним значениям А. Составить систему линз и повторить все измерения при двух значениях L. Вычислить фокусное расстояние системы линз. Рассчитать фокусное расстояние отрицательной линзы по формуле (2). Вывести формулы погрешности для расчета ошибок фокусных расстояний положительной и отрицательной линз и вычислить эти погрешности для одного значения L.
Источник
Собирающей линзы методом Бесселя
| Цель: | изучение метода Бесселя, определение фокусного расстояния линзы. |
| Оборудование: собирающая линза, осветитель, экран. |
Метод Бесселя позволяет определить фокусное расстояние линзы с большей точностью, чем при использовании формулы тонкой линзы (см. лабораторную работу 1). Это связано с тем, что в данном методе не нужно точно определять положение оптического центра линзы.
Порядок выполнения работы
1. Установить экран на расстоянии В от лампы осветителя (см. рисунок). Расстояние В задается преподавателем.
2. Перемещая линзу между осветителем и экраном, найти такое положение линзы, при котором на экране будет уменьшенное изображение нити накаливания лампы осветителя. Запомнить это положение.
 |
3. Перемещая линзу, найти новое ее положение, при котором на экране будет увеличенное изображение нити накаливания лампы осветителя. Запомнить это положение.
4. Найти расстояние l между положениями линзы.
5. Вычислить фокусное расстояние линзы по формуле:
6. Меняя расстояние между экраном и осветителем, дважды повторить измерения и вычислить фокусное расстояние (см. пп. 1—5). Данные занести в таблицу.
| Номер опыта | В, см | l, см | f, см | fср, см | Df, см | Dfср, см | d f |
7. Найти среднее значение фокусного расстояния:
8. Вычислить абсолютные погрешности каждого измерения фокусного расстояния
9. Вычислить среднее значение абсолютной погрешности:
10. Вычислить относительную погрешность измерения фокусного расстояния:
1. Дайте определение линзы.
2. Дайте определения фокуса, фокусного расстояния линзы.
3. Какое изображение называют действительным?
4. Какое изображение называют мнимым?
5. Какие линзы называют собирающими?
6. Какие линзы называют рассеивающими?
7. В чем заключается метод Бесселя?
8. В чем заключается преимущество метода Бесселя?
Источник
