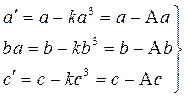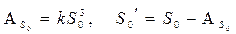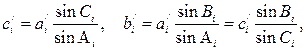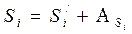Способ аддитаментов для решения треугольников

Способ аддитаментов

Как известно, основан на теореме синусов сферической тригонометрии, в которой тригонометрические функции малых аргументов представляют в виде ряда с удержанием двух членов разложений. В результате получают теорему синусов плоской тригонометрии

,

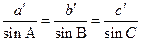
где a¢, b¢, c¢ – приведённые длины сторон треугольника, вычисляемые по формулам

Величина 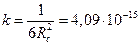для всей территории Беларуси, если длины сторон брать в метрах. А_а, А_в, А_с – аддитаменты сторон.

Порядок решения треугольников триангуляции:

1. Вычисляется аддитамента исходной стороны и вычитается из её длины, получается приведенная длина исходной стороны

2. По приведенной длине исходной стороны из решения треугольников по теореме синусов плоской тригонометрии последовательно вычисляются приведенные длины сторон треугольников (с контролем). Углы в треугольниках берут сферические уравненные (из способа Лежандра)

3. Вычисляются аддитаменты по приведенным длинам сторон и путём сложения с ними, получают точные значения сторон треугольника

При большом числе треугольников триангуляции или трилатерации их решение производится последовательно. В триангуляции, как известно, может быть измеренной или вычисленной длина одной стороны, соединяющая исходные пункты. Вначале решается треугольник, включивший исходную сторону, а затем решаются другие треугольники, смежные с уже решённым. В трилатерации решение треугольников может производиться в любой последовательности.

При вычислении аддитаментов предварительные значения длин сторон достаточно вычислять с округлением до десятков метров. Результаты вычислений необходимо оформить в виде таблицы.

В практике геодезических вычислений решение треугольников производят с контролем, применяя для этой цели оба способа. Расхождение в длинах сторон не должно превышать 0,001 м, а в углах 0,01² в сетях 1-2 классов.

Задание на выполнение работы:

Решить три треугольника звена триангуляции 1 класса по способу Лежандра и способу аддитаментов.

Исходные данные для выполнения лабораторных работ № 2 — 4:

Источник

Краткие теоретические сведения. Решение главной геодезической задачи на поверхности эллипсоида

Решение главной геодезической задачи на поверхности эллипсоида

Решение сферического треугольника по способу аддитаментов

Идея способа аддитаментов заключается в том, что стороны сферического треугольника a,b,c исправляют поправками, в результате чего получают стороны плоского треугольника a’,b’,c’ и неизвестные стороны сферического треугольника. Аддитаментами являются величины A_a=ka 3 , A_b=kb 3 , A_c=kc 3 , где k=1/6R 2 , R – средний радиус кривизны эллипсоида для района расположения треугольника. Значение величины можно принять постоянной для территории бывшего СССР и равной k=4.09×10 -15 . При этом длины сторон треугольника выражают в метрах.

Последовательность решения по способу аддитаментов:

1) Из исходной стороны c вычитают ее аддитамент A_c и получают сторону плоского треугольника c’.

2) По известным углам сферического треугольника и стороне c’ решают треугольник как плоский, используя теорему синусов, и находят остальные стороны плоского треугольника a’ и b’ : a’=c’sinA/sinC , b’=c’sinB/sinC

3) Полученные значения сторон исправляют их аддитаментами и находят искомые стороны сферического треугольника: a=a’+ka ’3 =a’+A_a , b=b’+kb ’3 =b’+A_b

Задание и исходные данные

Решить треугольник по теореме Лежандра и способу аддитаментов. Исходные данные: Bm =55°27’00» ; S_AB=30500,123+100·№, где № – номер варианта; f=0,0025290 ; A = 50°20’19.41» ; B = 62°12’44.54» ; C = 67°26’58.43»

Схема решения

Bm =	55°27’00»	A B C a c b
c =	30 500,123
Углы треугольника на эллипсоиде
A =	50°20’19.41»
B =	62°12’44.54»
C =	67°26’58.43»
Теорема Лежандра
Вычисление сферического избытка
f	0,0025290
cкм 2	930,258
sinA	0,7698311
sinB	0,8846817
sinC	0,9235423
ε	1,735»

Решение треугольника
Вершина	Измеренные углы сферического треугольника	Поправка из уравнивания -w/3	Уравненные углы сферического треугольника	-ε/3	Углы плоского треугольника	Синусы углов плоского треугольника
С	67°26’58.43»	-0,215»	67°26’58.22»	-0,578»	67°26’57.64»	0,92354083
A	50°20’19.41»	-0,215»	50°20’19.20»	-0,578»	50°20’18.62»	0,76982865
B	62°12’44.54»	-0,215»	62°12’44.33»	-0,578»	62°12’43.75»	0,88467987
Σ	180°00’02.38»	-0,65»	180°00’01.74»	-1,73»	180°00’00.00»
ε	1,73»
w=Σ-180-ε	0,65»
Стороны сферического треугольника
DII	33 025,202
a	25 423,747
b	29 216,732

Способ аддитаментов (Схема решения)
k =	4,09E-15
Вершина	Измеренные углы сферического треугольника	Поправка из уравнивания -w/3	Уравненные углы сферического треугольника	Синусы уравненных углов сферического треугольника	Стороны плоского треугольника	As	Стороны сфероидического треугольника
С	67°26’58.43»	-0,215»	67°26’58.22»	0,92354191	30 500,007	0,116	30 500,123
A	50°20’19.41»	-0,215»	50°20’19.20»	0,76983044	25 423,680	0,067	25 423,747
B	62°12’44.54»	-0,215»	62°12’44.33»	0,88468118	29 216,630	0,102	29 216,732
Σ	180°00’02.38»	-0,65»
ε	1,73»
w	0,65»

Определение координат некоторой точки по известным координатам других точек к измеренным или заданным угловым к линейным величинам называется главной геодезической задачей.

Такая задача может быть поставлена в различных координатных системах. В высшей геодезии принято решать эту задачу в геодезической системе координат, которая предполагает известными размеры и ориентировку конкретного референц-эллипсоида.

Главную геодезическую задачу принято рассматривать в виде двух задач: прямой и обратной.

Прямая геодезическая задача состоит в том, чтобы по известным координатам начальной точки B₁, L₁ , прямому азимуту A₁₂ и расстоянию S₁₂ определить координаты конечной точки B₂, L₂ и обратный азимут A₂₁.

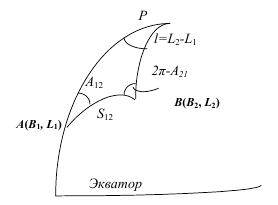
Обратная геодезическая задача заключается в том, чтобы по координатам начальной и конечной точек B₁, L₁, B₂, L₂ определить расстояние S₁₂ между ними и азимуты A₁₂, A₂₁ (см. рис).

В геодезической практике прямую и обратную геодезические задачи приходится решать для различных длин геодезических линий. На практике установилась определенная градация возможных расстояний, для каждой из которых существует наиболее удобный метод решения главных геодезических задач.

· Малые расстояния (от 20 до 200 км) встречаются при вычислении сторон треугольников и замыкающих звеньев триангуляции I класса.

· Средние расстояния (от 200 до 800 км) имеют место при вычислении диагоналей полигонов триангуляции 1 класса, при обработке астрономо-геодезической сети, при развитии динамической (ракетной) триангуляции, радиогеодезических сетей и других задач.

· Большие расстояния (более 800 км) встречаются при ориентировке референц-эллипсоида, при геодезическом соединении материков методом космической триангуляции, в радионавигации, при установлении единой координатной системы. в целях слежения за управляемыми ракетами и т. д.

Для решения главных геодезических задач необходимо установить уравнения связи исходных и определяемых величин. Наиболее простой и естественный способ установления таких уравнений связи и в конечном итоге решения главных геодезических задач заключается в непосредственном решении треугольника APB (см. рис.), в котором исходные данные и определяемые неизвестные как в прямой, так и в обратной задачах являются элементами этого треугольника. Например, в случае прямой геодезической задачи исходными данными являются стороны S₁₂, AP и угол A₁₂. Из решения треугольника получаются другие его элементы l, A₂₁, BP, с помощью которых определяют искомые величины L₂=L₁+l, B₂=90°–BP.

Такой путь решения главных геодезических задач называется прямым. Однако в связи с большими сторонами полярного треугольника APB, достигающими нескольких тысяч километров, его нужно рассматривать как сфероидический. Это обстоятельство значительно усложняет решение и требует использования 10-значных таблиц тригонометрических функций. Поэтому применяют другой путь решения, который называют косвенным.

Косвенный путь решения главных геодезических задач заключается в определении разностей широт, долгот н азимутов, на основании уравнений связи этих величин с исходными данными. Например, для прямой задачи определяют

Задание и исходные данные

Прямая задача

В треугольнике ABC из решения прямой геодезической задачи вычислить геодезические координаты каждой вершины. Значения длин сторон и уравненных сферических углов треугольника взять из предыдущей работы (Решение геодезических треугольников).

1) Используя B_A= 52°20’00.000», L_A= 65°12’34.567», A_AB= 12°34’56.789»и сторону S_AB, согласно своего варианта в работе «Решение геодезических треугольников», получить из решения прямой геодезической задачи координаты точки B (B_B, L_A) и обратный азимут А_BA.

2) Вычислить азимут стороны A_BC = A_BA –

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Решение сферического треугольника по теореме лежандра и способу аддитаментов

РЕШЕНИЕ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА ПО ТЕОРЕМЕ

ЛЕЖАНДРА И СПОСОБУ АДДИТАМЕНТОВ

Треугольник триангуляции 1-го класса

Определить координаты точки С.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

При помощи программы Prima решаем обратную геодезическую задачу и определяем длину стороны с:

Таблица 1

Решение обратной геодезической задачи

2. Теорема Лежандра утверждает: если стороны плоского и сферического треугольника соответственно равны, то углы плоского треугольника равны углам сферического, уменьшенным на одну треть сферического избытка.

Если обозначить А, В, С углы сферического треугольника, полученные из измерений, а — сферический избыток и вычислить:

; ; ;

;

(вычисляется по средней широте),

то А / , В / , С / есть углы плоского треугольника, стороны которого равны соответственно сторонам сферического треугольника.

Вычисление сферического избытка выполняется в таблице 2.

Таблица 2

Вычисление сферического избытка

3. Решение треугольника триангуляции по теореме Лежандра выполняется в таблице 3.

Стороны плоского треугольника вычисляем по теореме синусов, используя уравненные углы плоского треугольника и известную сторону.

4.Решим сферический треугольник по способу аддитаментов, принимая следующее утверждение:

если углы плоского треугольника равны соответствующим углам сферического, то стороны плоского треугольника меньше соответствующих сторон сферического на величину аддитамента.

Для сторон треугольников меньше 100 км аддитаменты вычисляются по формулам:

K =1/6 R 2 (значение длин сторон берется в км, аддитаменты получаем в м).

Вычисления производим в таблице 4.

По известной стороне сферического треугольника находим аддитамент и сторону плоского треугольника: S _{плоского}= S _{сферического}-А.

Применяя теорему синусов, по известной стороне плоского треугольника и по углам находим значения недостающих сторон плоского треугольника. Вычисляем аддитаменты найденных сторон и определяем стороны сферического треугольника по формулам: S _{сферического}=Sплоского+А.

5. Вычисляем азимуты направлений АС и ВС, используя уравненные углы сферического треугольника и азимут направления АВ.

6. Используя программу Prima решаем прямую геодезическую задачу и вычисляем широту и долготу точки С от двух исходных точек (А и В).

Решение треугольника триангуляции по теореме Лежандра

Источник

Читайте также:  Способы познания мира человеком для детей