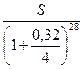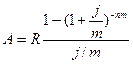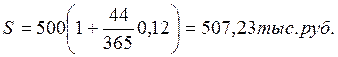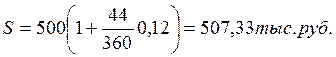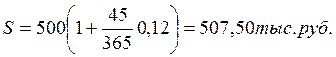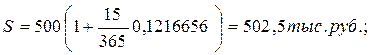Способ 365 360 это

Финансовая математика 03

1. Предприятие обратилось 1 марта в банк за кредитом в 150 тыс. руб., обязуясь вернуть сумму с процентами в конце года (31 декабря). Какой способ начисления простых процентов 365/365, 365/360 или 360/360 выгоден для предприятия и какой — для банка, если используется простая процентная ставка 26 % годовых и год не високосный?

Для нахождения наращенной суммы воспользуемся формулой наращения по простым процентам, или формулой простых процентов:

S = P(1+i,где

S – наращенная сумма;

P – первоначальная сумма кредита;

I – процентная ставка;

T – период начисления в днях;

K – продолжительность года в днях.

1) английскую практику начисления процентов или точные проценты с точным числом дней ссуды, когда продолжительность года и продолжительность ссуды берутся точно по календарю. (365/365)

01.03 – 60 день в году

T = 365 — 60 = 305 дней

S = 150 000 (1+0,26) = 182 589,04 руб.

2) французская практика начисления процентов или Обыкновенные проценты с точным числом дней ссуды, когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю. (365/360)

S = 150 000 (1+0,26) = 183 041,67 руб.

3) германская практика начисления процентов или обыкновенные проценты с приближенным числом дней ссуды или, когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней. (360/360)

T = 30 – 1 +30*8+31= 300 дней

S = 150 000 (1+0,26) = 182 500 руб.

Ответ: для предприятия выгоден способ начисления простых процентов 360/360, т. к. ему необходимо будет вернуть 182500 руб. Для банка выгоден способ начисления простых процентов – 365 / 360, т. к. предприятие вернет банку 183 041,67 руб.

2. В банк предлагаются для учета два векселя: на сумму 30 тыс. руб. со сроком погашения через 60 дней и на сумму 34 тыс. руб. со сроком погашения через 240 дней. При каком способе дисконтирования: а) по учетной ставке, б) по процентной ставке банк при учете этих векселей выплатит одинаковые суммы, если расчетное число дней в году равно 360?

Т. к. выплаты одинаковы, составим следующие равенства:

А) Выплаты по учтенной ставке определяются по следующей формуле:

P = S (1 — d,

Где S – номинал векселя;

Р – сумма, полученная векселедержателем;

D – простая учетная ставка;

t –срок погашения в днях;

K – продолжительность года в днях.

30 (1 — d = 34 (1 — d

30 — 5d = 34 – 22,67d

— 5d + 22,67d = 34 – 30

D = 0,2264 или 22,64%

Б) Выплаты по процентной ставке определяются по следующей формуле:

Р = ,

Где i – простая процентная ставка.

= >

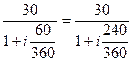
30 + 20,01i = 34+5,678i

20,01i – 5,678i = 34 – 30

14,332i = 4 / 14,332

I = 0,2791 или 27,91%

Ответ: при учете векселей выплатит одинаковые суммы а) при простой учетной ставке равной 22,64%, б) при простой процентной ставке – 27,91%

3. Банк предоставил ссуду в размере 150 тыс. руб. на 39 месяцев под процентную ставку 30% годовых на условиях единовременного возврата основной суммы долга и начисленных сложных процентов. Какую сумму предстоит вернуть банку при различных вариантах начисления сложных процентов: а) годовом; б) полугодовом; в) ежеквартальном.

Наращенная сумма определяется по следующей формуле:

S = P,

Где S – наращенная сумма;

Р – первоначальная сумма;

J – номинальная ставка процентов;

M – интервал начисления процентов.

39 месяцев – это 3,25 года

А) S = 150000351890,19 руб.

Б) S = 150 000372 072,20 руб.

В) S = 150000384 061,96 руб.

Ответ: наращенная сумма равна а) 351890,19 руб.; б) 372072,20 руб.; в) 384061,96 руб.

4. Имеется обязательство выплатить суммы 60 тыс. руб. и 90 тыс. руб. соответственно через 3 года и 5 лет. По обоюдному согласию стороны пересматривают порядок выплат: 15 тыс. руб. выплачиваются через 1 год 6 месяцев, 45 тыс. руб. — через 2 года, 50 тыс. руб. — через 6 лет, остаток долга погашается через 7 лет. Определите величину четвертого платежа, если на деньги начисляются ежеквартально сложные проценты по годовой номинальной процентной ставке 32 %

Sj1 = 60 тыс. руб.

Sj2 = 90 тыс. руб.

Уравнение эквивалентности платежей общего в вида при использовании сложной процентной ставке имеет вид:

Где Sj и nj – параметры заменяемых платежей;

Sk и nk – параметры заменяющих платежей.

= +

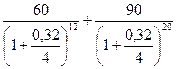
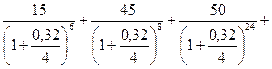
23,81+19,31 = 9,4+24,32+7,89 + 0,12S

0,12S = 43,12 – 41,61

S = 12,58 тыс. руб.

.Ответ: величина четвертого платежа равна 12,58 тыс. руб.

5. Банк предлагает ренту постнумерандо на 10 лет с квартальной выплатой 4 тыс. руб. Годовая процентная ставка в течение всего периода остается постоянной, и сложные проценты начисляются ежеквартально. По какой цене можно приобрести эту ренту сейчас, если выплаты начнут осуществляться немедленно, а сложная процентная ставка равна 32 % годовых?

Так как количество выплат в год равно интервалу начисления процентов (p=m), современную стоимость ренты определим по следующей формуле:

Где А –современная стоимость ренты;

R – размер платежа; ты

J – номинальная ставка процентов;

M – интервал начисления процентов.

47700 руб.

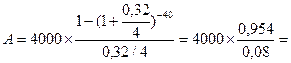
Источник

Три метода начисления процентов в зависимости от выбранного периода

При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражают дробным числом как отношение числа дней функционирования сделки к числу дней в году:

где t — число дней функционирования сделки (число дней, на которое предоставили кредит);

К— временная база (число дней в году).

В этом случае формула (1.4) примет вид:

(1.5)

В ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года (К) принимается равной 360 дням. Это так называемая германская практика. Проценты, рассчитанные с временной базой К= 360 дней и приближенным числом дней в месяце (30 дней), называются обыкновенными, или коммерческими.

Существует «французская практика», когда продолжительность года принимается равной К= 360 дней, а продолжительность месяцев в днях соответствует календарному исчислению. Такой метод начисления процентов называют также обыкновенными процентами с точным числом дней ссуды.

И наконец, в ряде стран используется «английская практика», учитывающая продолжительность года в K=365 дней, а продолжительность месяцев — в днях, также соответствующих календарному исчислению, как и при использовании «французской практики», т.е. 28, 29, 30 и 31 день.

В этой связи различают три метода процентных расчетов, которые зависят от выбранного периода начисления.

1. Точные проценты с точным числом дней ссуды («английская практика»). При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения кредита), продолжительность года принимается равной К=365 (366) дней. В этом случае применяется обозначение 365/365.

2. Обыкновенные проценты с точным числом дней ссуды («французская практика»); величина t рассчитывается, как и в предыдущем случае. В этом случае применяется обозначение 365/360.

3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется количеством месяцев по 30 дней в каждом? начиная с момента выдачи ссуды и до момента се погашения и точным числом дней ссуды в неполном месяце; продолжительность года К= 360 дней. В этом случае применяется обозначение 360/360.

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Пример 1.4.

Банк выдал кредит 18 января в размере 500,0 тыс. руб. Срок возврата кредита — 3 марта; процентная ставка — 12,0% годовых; год невисокосный. Определить сумму долга, подлежащую возврату. Необходимо рассчитаем се тремя методами.

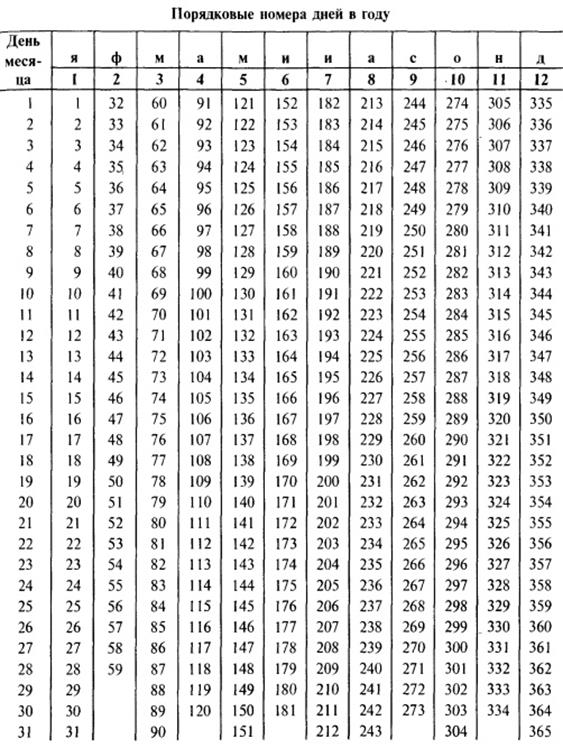
Точное число дней ссуды определим по табл. 1 (Приложение 1): 62–18=44 дня.

Такой же результат мы получим, рассчитывая число дней по календарю;

С 18.01 по 31.01 включительно— 14дней;

февраль — 28 дней;

t=45-1=44 дня.

Приближенное число дней ссуды (продолжительность каждого месяца принимается за 30 дней):

январь — 13 дней;

февраль— 30 дней;

t=46-1=45 дней.

Возможные варианты расчета наращенной суммы:

1) по точным процентам с точным числом дней ссуды:

2) по обыкновенным процентам с точным числом дней ссуды:

3) по обыкновенным процентам с приближенным числом дней ссуды:

Приведенный пример свидетельствует, что для кредиторов наиболее предпочтительным является третий вариант начисления процентов.

Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I₃₆₀ и I₃₆₅) при равном числе дней ссуды (t) существуют следующие соотношения:

И . (1.6)

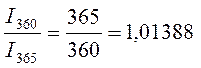
Данные соотношения характеризуют зависимость величины процентного дохода от выбранной временной базы.

По данным примера 1.4(2).

I₃₆₀=507,33-500=7,33тыс.руб I₃₆₅=507,23-500=7,23тыс.руб

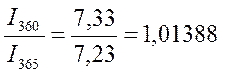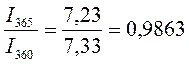Эти соотношения также могут быть использованы при определении эквивалентных процентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах: ;

Пример 1.5.

При выдаче ссуды 500,0 тыс. руб. на 15 дней по ставке 12% годовых, при К=360 дней, наращённая сумма и процентный доход соответственно составят:

Определить величину процентной ставки, обеспечивающей такой же процентный доход при временной базе К = 365 дней:

i₃₆₅=1,01388*0,12=0,1216656

Проверим это вычисление:

Как указывалось ранее, при заключении кредитного соглашения может быть установлена постоянная на весь период процентная ставка или изменяющаяся (переменная) процентная ставка. При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная сумма определяется по формуле

(1.8)

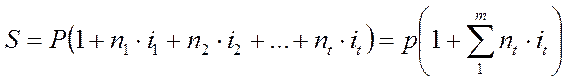
Где i_t — ставка простых процентов в периоде t;

n_t — продолжительность начисления ставки i_t ;

m — число периодов начисления процентов.

Пример 1.6.

Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: в первое полугодие процентная ставка 12,0% годовых, каждый следующий квартал ставка возрастает на 0,5%, Проценты начисляются только на первоначально внесенную сумму вклада.

Определить наращённую за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб.:

Решение:

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник