Спектральный способ представления гармонических колебаний

Спектральное представление сигналов

Любой сигнал можно разложить на составляющие. Такое разложение сигнала называется спектральным. При этом сигнал можно представить в виде графика зависимости параметров сигнала от частоты, такая диаграмма называется спектральной или спектром сигнала.

Спектр сигнала — это совокупность простых составляющих сигнала с определенными амплитудами, частотами и начальными фазами.
Между спектром сигнала и его формой существует жесткая взаимосвязь: изменение формы сигнала приводит к изменению его спектра и наоборот, любое изменение спектра сигнала приводит к изменению его формы. Это важно запомнить, поскольку при передаче сигналов в системе передачи, они подвергаются преобразованиям, а значит, происходит преобразование их спектров.

Различают два вида спектральных диаграмм:
— спектральная диаграмма амплитуд;
— спектральная диаграмма фаз.

В спектральной диаграмме амплитуд — отображаются все составляющие со своими амплитудами и частотами.
В спектральной диаграмме фаз — отображаются все составляющие со своими начальными фазами и частотами.
Любой сигнал имеет одну спектральную диаграмму амплитуд и одну спектральную диаграмму фаз, в составе которых может содержаться множество составляющих.

Не зависимо от того, какой спектр (амплитуд или фаз), он изображается в виде множества линий — составляющих. В спектре амплитуд высота спектральной линии равна амплитуде составляющей сигнала, а в спектре фаз — начальной фазе составляющей. Причем: в спектре амплитуд все составляющие имеют положительные значения, а в спектре фаз как положительные, так и отрицательные. Если амплитуда спектральной составляющей имеет отрицательный знак, то в спектре амплитуд она берется по модулю, а в спектре фаз знак составляющей изменяется на противоположный.

Классификация спектров сигналов.
1. По виду спектры бывают дискретными (линейчатыми) или сплошными.
Дискретным является спектр, у которого можно выделить отдельные составляющие.
Сплошным является спектр, у которого нельзя выделить отдельные составляющие, так как они расположены настолько близко, что сливаются друг с другом.
2. По диапазону частот различают спектры ограниченные и неограниченные.
Ограниченным является спектр, у которого вся энергия сигнала (все спектральные составляющие) находятся в ограниченном диапазоне частот (fmax ? ?).
Неограниченным является спектр, у которого вся энергия сигнала находится в неограниченном диапазоне частот (fmax ? ?). На практике такие спектры ограничивают.

Спектральное представление периодических сигналов

1. Гармоническое колебание.
Математическая модель гармонического колебания имеет вид:

u(t)=Ums sin (?st+?s) (11)

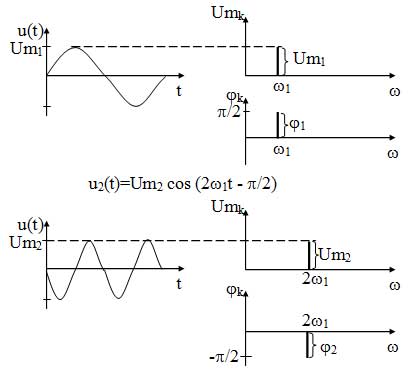
Как видно из математической модели, в спектре данного колебания присутствует одна гармоническая составляющая, которая находится на частоте ?s. Высота составляющей в спектре амплитуд равна амплитуде колебания Ums, а в спектре фаз — начальной фазе колебания ?s. Причем при построении спектра необходимо учитывать связь между временной диаграммой сигнала и спектром амплитуд. Амплитуда составляющей спектра должна по высоте соответствовать амплитуде колебания на временной диаграмме.
Необходимо отметить, что при увеличении частоты сигнала, его составляющая будет удаляться по оси частот от нуля (рисунок 13).

Рисунок 13 — Спектральное представление гармонических колебаний

Как видно из рисунков, спектр гармонического колебания является дискретным и ограниченным.
2. Периодические, негармонические сигналы.
Основной особенностью спектрального представления таких сигналов является наличие в их спектре множества спектральных составляющих. Такие сигналы могут быть описаны рядом Фурье, согласно которому: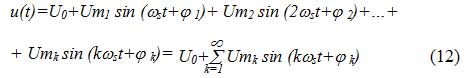
т. е. сигнал может быть представлен суммой постоянной составляющей и множества гармонических составляющих.

Преобразуем данный ряд, используя тригонометрическое свойство

sin(x+y) = sin x cos y + cos x sin y (13)

Полагая что x=?k и y=k?ct получим:

Поскольку Umk и ?k являются параметрами ряда, то их можно обозначить коэффициентами

Umk sin ? k = ak; Umk cos ?k = bk (15)

Тогда ряд примет вид:

Параметры ряда можно определить через коэффициенты ak и bk:

где k=1, 2, 3 …

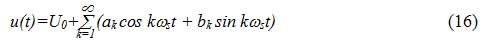
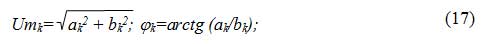
Амплитуда постоянной составляющей и коэффициенты могут быть определены через значение сигнала u(t):

Из ряда следует, что если описываемый сигнал является четной функцией f(t)=f(-t), то ряд будет иметь только косинусоидальные составляющие, так как bk=0, если нечетная функция (f(t) ? f(-t)), то рад содержит только синусоидальные составляющие (ak=0).
Рассмотрим спектральное представление периодических, негармонических сигналов на примере периодической последовательности прямоугольных импульсов (ПППИ).
При построении спектра необходимо рассчитать следующие параметры:
а) скважность сигнала:

б) значение постоянной составляющей:

в) частоту первой гармоники спектра, которая равна частоте сигнала:

г) амплитуды гармонических составляющих спектра:

При построении спектра необходимо отметить следующие особенности:
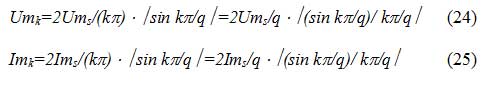
1. Все гармонические составляющие находятся на частотах, кратных частоте первой гармоники (2?1, 3?1, 4?1 и т. д.);
2. Для спектра амплитуд:
а) спектр ПППИ имеет лепестковый характер, т. е. в спектре можно выделить множество «лепестков»;
б) количество гармонических составляющих в лепестке зависит от скважности и равно q — 1;
в) амплитуды гармонических составляющих, находящихся на частотах, кратных скважности, равны нулю;
г) форма спектра обозначается огибающей — пунктирной линией, плавно соединяющей вершины гармонических составляющих;
д) точка, из которой исходит огибающая, равна 2U0 или 2I0.
3. Для спектра фаз:
а) все гармонические составляющие, на частотах, не кратных скважности, имеют одинаковую высоту, равную ?/2 (90°);
б) все гармонические составляющие в одном лепестке имеют одинаковый знак, а в соседних противоположный.
в) составляющие на частотах кратных скважности имеют начальную фазу равную нулю.
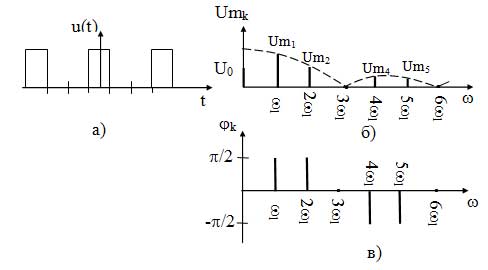
Спектры ПППИ при скважности q=3 представлены на рисунке 14.
Как видно из диаграмм спектр ПППИ является дискретным и неограниченным. Поэтому за ширину спектра принимают диапазон частот, в пределах которого находится два первых лепестка, т. к. в них содержится около 95% энергии сигнала:

Рисунок 14 — Спектральное представление ПППИ: а) временная диаграмма; б) спектральная диаграмма амплитуд; в) спектральная диаграмма фаз

Как видно из формулы ширина спектра ПППИ зависит только от длительности импульса и не зависит от его периода.
3. Непериодические сигналы.
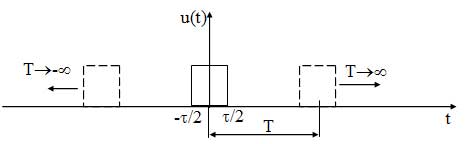
Поскольку в непериодических сигналах нельзя выделить период, т. к. Т. то рассчитать и построить спектр тем же методом, что и для периодических сигналов нельзя. Однако знать спектр таких сигналов необходимо, т. к. все информационные сигналы являются непериодическими. Для построения спектра непериодического сигнала производят следующую процедуру: сигнал мысленно представляют как периодический с произвольным периодом, ддля которого строят спектр. Затем осуществляют предельный переход устремляя период к бесконечности (Т??) (рисунок 15). При этом частота первой гармоники и, соответственно, расстояние между гармоническими составляющими стремится к нулю (f1=1/Т), поэтому все составляющие сливаются друг с другом и образуют сплошной спектр.

Рисунок 15 — Импульсный сигнал u(t) и его представление периодическим сигналом

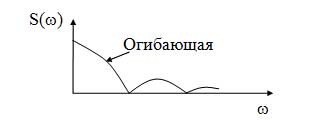
Форма спектра непериодических сигналов обозначается огибающей (сплошной линией) (рисунок 16).

Рисунок 16 — Спектральная диаграмма непериодического сигнала

Ряд Фурье, для таких сигналов, также нельзя записать, т. к. в этом случае амплитуда постоянной составляющей и коэффициенты ak и bk равны нулю. В этом случае значение сигнала в любой момент времени также равно нулю, что является не верным. Поэтому для таких сигналов используют преобразования Фурье:

Выражение (27) является обратным преобразованием, а (28) прямым преобразованием Фурье.
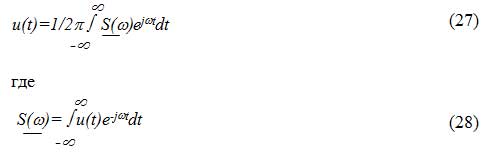
Величина S(?) является комплексной спектральной плотностью непериодического сигнала u(t). Она равна:

где S(?) спектральная плотность амплитуд или амплитудный спектр непериодического сигнала, а ?(?) — фазовый спектр непериодического сигнала.
Спектральная плотность амплитуд непериодического сигнала на любой частоте ? равна суммарной амплитуде составляющих находящихся в малой полосе ?? в окрестностях частоты ? пересчитанных на 1 Герц.
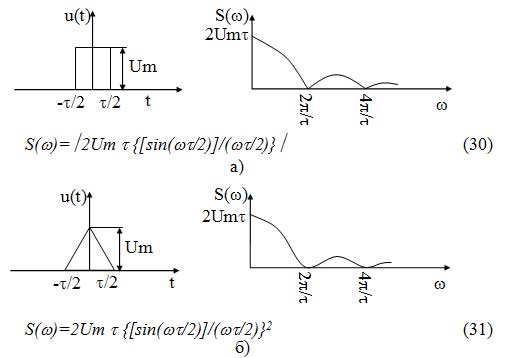
Временные диаграммы и спектральные плотности амплитуд для прямоугольного и треугольного импульсов представлены на рисунке 18:

Рисунок 18 — Спектральное представление непериодических сигналов: а) прямоугольный импульс; б) треугольный импульс

Источник

Спектральное представление колебаний: периодических, непериодические колебания

Спектральное представление колебаний

Спектральное представление периодических колебаний

При формировании и обработке сигналов часто приходится иметь дело с колебаниями, описываемыми периодическими функциями вида S(t) = S(t±kT), где k = 1, 2, …; Τ — период (рис. 2.9).

Зададим на отрезке полную систему тригонометрических ортогональных функций:

где ω1 = 2π / T — основная частота.

Выбор такого базиса наиболее распространен, так как в результате его использования обеспечиваются:
• сравнительная простота формирования гармонических колебаний;
• инвариантность сигналов относительно их преобразований в линейных электрических цепях (ЛЭЦ). При прохождении через ЛЭЦ изменяются только амплитуда и начальная фаза составляющих.

В этом случае для сигнала S(t) обобщенный ряд Фурье будет иметь вид
Здесь коэффициенты разложения
откуда видно, что периодический сигнал содержит постоянную составляющую и бесконечный набор гармонических колебаний с частотами (Формула), которые являются кратными основной частоте.

Рис. 2.9. Пример периодической функции

Рис. 2.10. Амплитудная спектральная диаграмма периодического сигнала

Представим коэффициенты разложения в виде
где Ак — амплитуда; фк — начальная фаза.

Тогда ряд Фурье можно записать в другой эквивалентной форме:
Выражение (2.12) можно интерпретировать графически как сумму гармоник с частотами, кратными основной частоте f1 = 1 / T , амплитудами Аk и начальными фазами φk. При этом различают амплитудный и фазовый спектры.

Амплитудный спектр показан на рис. 2.10.

Рассмотрим теперь комплексную форму записи сигнала в виде ряда Фурье. В этом случае в качестве базисных функций применяются комплексные экспоненты:

где k = 0, ±1, ±2, …; j — мнимая единица.

Такая система также является полной.

Соответственно обобщенный ряд Фурье, известный как ряд Фурье в комплексной форме, приобретает следующий вид:
Здесь комплексная амплитуда k-й гармоники
связана с Аk, αk, bk, φk следующими выражениями:
Из этих выражений следует, что фазовый угол φk является нечетной функцией относительно k, т. е. относительно частоты, а модуль комплексной амплитуды Аk — четной.

Как видно из соотношения (2.13), суммирование распространено на положительные (k) и отрицательные (−k) частоты. Последние имеют фиктивный характер. Действительную составляющую (Формула) сигнала с частотой (Формула) получают как сумму двух комплексных функций:
т. е. происходит взаимное уничтожение мнимых частей.

Отметим также, что спектр периодического сигнала является дискретным и бесконечным. С увеличением периода следования сигналов разность частот между соседними гармониками уменьшается, т. е. спектр сгущается.

Из формул (2.11) и (2.14) видно, что изменение периода T сказывается на значении амплитуд спектральных составляющих: с увеличением Τ амплитуды уменьшаются. Однако форма спектра амплитуд при этом сохраняется.

Пример 2.3. Определим спектр периодической последовательности прямоугольных импульсов с амплитудой Е, длительностью (Формула) и периодом следования Т.

Итак, пусть
По формуле (2.14) находим
Комплексная амплитуда (Формула) пропорциональна функции вида (Формула) и содержит только вещественную часть, т. е.
Начальные фазы гармоник следующие: φ = 0, в интервалах частот (Формула), где n = 0, 2, 4, …

φk = ±π в интервалах частот (Формула), n = 1, 3, 5, …

С учетом этих соотношений ряд Фурье (2.13) для последовательности прямоугольных импульсов можно записать в виде
Пример 2.4. Периодическая последовательность двухполярных импульсов ±Е задана в виде
Представим S1(t) как результат суммирования однополярных импульсов с амплитудой 2Е и постоянной составляющей −Е, т. е. получим выражение
S1(t) = 2S(t) − E.

Подставив в это выражение S1(t) в виде (2.15), получим ряд Фурье для S1(t):
Спектральное представление непериодических колебаний

Рассмотренные ранее периодические сигналы на практике почти не встречаются. В подавляющем большинстве случаев в теории и технике связи приходится иметь дело с сигналами и помехами, которые по существу являются непериодическими и к которым аппарат рядов Фурье не применим. Поэтому вместо них используют интегралы Фурье. Такое представление получают посредством перехода от ряда Фурье при стремлении периода повторения сигнала к бесконечности, т.е. T → ∞ или f1 = 1 / T = ω1 / (2π) → 0.

Рассмотрим вновь ряд Фурье в экспоненциальной форме:
где Δω = ω1 = [kω1 − (k − 1)ω1] — разность между частотами соседних гармоник, k = 1, 2, …

Определим комплексную спектральную плотность в виде

При Δω → 0 интервалы между соседними гармониками неограниченно сокращаются, поэтому сумму можно заменить интегралом:
Для нахождения комплексной спектральной плотности S(jω), или комплексного спектра, можно использовать выражение

которое следует из формулы (2.14) для комплексной амплитуды и отличается от нее только наличием множителя 2 / Т.

Выражения (2.17) и (2.18) имеют фундаментальное значение в ТЭС. Первое из них называется «обратным преобразованием Фурье» для сигнала S(t), или «операцией синтеза», поскольку с его помощью сигнал восстанавливается (синтезируется) из спектральных составляющих. Второе выражение называется «прямым преобразованием Фурье», или «операцией анализа» сигнала на основе определения его спектральных составляющих. В символической записи соответствие между сигналом S(t) и его преобразованием Фурье S(jω) отображается следующим образом: S(t) ⇄ S(jω).

С учетом четности модуля S(ω) и нечетности фазы φ(ω) обратное преобразование Фурье (2.17) можно записать в виде.

В соответствии с выражением (2.17) и последней формулой непериодическое колебание S(t) можно рассматривать как сумму комплексных экспоненциальных составляющих или сумму гармонических составляющих , частоты которых располагаются бесконечно близко друг к другу. На основании этого можно говорить о непрерывном, или сплошном, спектре непериодического колебания.

Бесконечно малые амплитуды составляющих определяются выражением Am = с|S(jω)|dω, где (Формула) для формулы (2.17) или с учетом четности модуля S(ω), т.е. |S(jω)| отражает спектральную (частотную) плотность амплитуд составляющих. Другими словами, |S(jω)| — это амплитуда, отнесенная к бесконечно малой полосе частот dω.

Особенностью комплексного спектра является его распространение как в положительной, так и в отрицательной области частот. Следовательно, двум составляющим частот ω и −ω со спектральной плотностью комплексного спектра соответствует одна гармоническая составляющая частоты ω со спектральной плотностью |S(jω)|.

Сопоставив формулы (2.18) и (2.14) для непериодического колебания и периодического колебания, полученного из исходного непериодического сигнала посредством его периодического продолжения, можно сделать вывод о том, что спектры таких колебаний совпадают по форме и отличаются лишь масштабом.

В табл. 2.1 приведены результаты расчетов S(jω) для колебаний (импульсов) различной формы.

Источник